Partitioning or Classifying a Set

Problem

You want to partition a Set or array based on some attribute of its elements. All elements that go "together" in some code-specific sense should be grouped together in distinct data structures. For instance, if you're partitioning by color, all the green objects in a Set should be grouped together, separate from the group of all the red objects in the Set.

Solution

Use Set#divide, passing in a code block that returns the partition of the object it's passed. The result will be a new Set containing a number of partitioned subsets of your original Set.

The code block can accept either a single argument or two arguments.[3] The single-argument version examines each object to see which subset it should go into.

[3] This is analogous to the one-argument code block passed into Enumerable#sort_by and the two-argument code block passed into Array#sort.

	require 'set' 
	s = Set.new((1..10).collect)
	# => #

	# Divide the set into the "true" subset and the "false" subset: that
	# is, the "less than 5" subset and the "not less than 5" subset.
	s.divide { |x| x < 5 }
	# => #, #}>

	# Divide the set into the "0" subset and the "1" subset: that is, the
	# "even" subset and the "odd" subset.
	s.divide { |x| x % 2 }
	# => #, #}>

	s = Set.new([1, 2, 3, 'a', 'b', 'c', -1.0, -2.0, -3.0])
	# Divide the set into the "String subset, the "Fixnum" subset, and the
	# "Float" subset.
	s.divide { |x| x.class } 
	# => #,
	# => #,
	# => #}>

For the two-argument code block version of Set#divide, the code block should return true if both the arguments it has been passed should be put into the same subset.

	s = [1, 2, 3, -1, -2, -4].to_set

	# Divide the set into sets of numbers with the same absolute value.
	s.divide { |x,y| x.abs == y.abs }
	# => #, 
	# => #, 
	# => #,
	# => #}>

	# Divide the set into sets of adjacent numbers 
	s.divide { |x,y| (x-y).abs == 1 }
	# => #,
	# => #,
	# => #}>

If you want to classify the subsets by the values they have in common, use Set#classify instead of Set#divide. It works like Set#divide, but it returns a hash that maps the names of the subsets to the subsets themselves.

	s.classify { |x| x.class }
	# => {String=>#,
	# => Fixnum=>#,
	# => Float=>#}

 

Discussion

The version of Set#divide that takes a two-argument code block uses the tsort library to turn the Set into a directed graph. The nodes in the graph are the items in the Set. Two nodes x and y in the graph are connected with a vertex (one-way arrow) if the code block returns true when passed |x,y|. For the Set and the two-argument code block given in the example above, the graph looks like Figure 4-1.

Figure 4-1. The set {1, 2, 3, -1, -2, -4} graphed according to the code block that checks adjacency

The Set partitions returned by Set#divide are the strongly connected components of this graph, obtained by iterating over TSort#each_strongly_connected_component. A strongly connected component is a set of nodes such that, starting from any node in the component, you can follow the one-way arrows and get to any other node in the component.

Visually speaking, the strongly connected components are the "clumps" in the graph. 1 and 3 are in the same strongly connected component as 2, because starting from 3 you can follow one-way arrows through 2 and get to 1. Starting from 1, you can follow one-way arrows through 2 and get to 3. This makes 1, 2, and 3 part of the same Set partition, even though there are no direct connections between 1 and 3.

In most real-world scenarios (including all the examples above), the one-way arrows will be symmetrical: if the code returns true for |x,y|, it will also return true for |y,x|. Set#divide will work even if this isn't true. Consider a Set and a divide code block like the following:

	connections = { 1 => 2, 2 => 3, 3 => 1, 4 => 1 }
	[1,2,3,4].to_set.divide { |x,y| connections[x] == y }
	# => #, #}>

The corresponding graph looks like Figure 4-2.

Figure 4-2. The set {1,2,3,4} graphed according to the connection hash

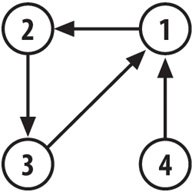
You can get to any other node from 4 by following one-way arrows, but you can't get to 4 from any of the other nodes. This puts 4 is in a strongly connected componentand a Set partitionall by itself. 1, 2, and 3 form a second strongly connected componentand a second Set partitionbecause you can get from any of them to any of them by following one-way arrows.

Implementation for arrays

If you're starting with an array instead of a Set, it's easy to simulate Set#classify (and the single-argument block form of Set#divide)with a hash. In fact, the code below is almost identical to the current Ruby implementation of Set#classify.

	class Array
	 def classify
	 require 'set'
	 h = {}
	 each do |i|
	 x = yield(i)
	 (h[x] ||= self.class.new) << i
	 end
	 h
	end

	 def divide(&block)
	 Set.new(classify(&block).values) 
	 end
	end

	[1,1,2,6,6,7,101].divide { |x| x % 2 }
	# => #

There's no simple way to implement a version of Array#divide that takes a two-argument block. The TSort class is Set-like, in that it won't create two different nodes for the same object. The simplest solution is to convert the array into a Set to remove any duplicate values, divide the Set normally, then convert the partitioned subsets into arrays, adding back the duplicate values as you go:

	class Array
	 def divide(&block)
	 if block.arity == 2
	 counts = inject({}) { |h, x| h[x] ||= 0; h[x] += 1; h}
	 to_set.divide(&block).inject([]) do |divided, set|
	 divided << set.inject([]) do |partition, e|
	 counts[e].times { partition << e } 
	 partition
	 end
	 end
	 else
	 Set.new(classify(&block).values) 
	 end
	 end
	end

	[1,1,2,6,6,7,101].divide { |x,y| (x-y).abs == 1 }
	# => [[101], [1, 1, 2], [6, 6, 7]]

Is it worth it? You decide.