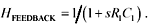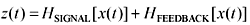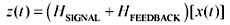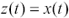Limits to Attainable Distance

In the pcb environment two factors limit the distance at which you can send reliable information: sensitivity and dispersion.

As you stretch the channel length to extreme distances, sensitivity-limited systems (also called loss-limited systems) fail due to insufficient signal amplitude at the receiver. This definition infers that at the limit of operating distance, the received signal would be reliably detectable if amplified. Such systems display an eye pattern with a good eye opening and a reasonable amount of jitter at the receiver, but too small a signal level to properly activate the receiver circuit.

Common causes of poor sensitivity include

1. Poor control over the receiver switching thresholds. This problem is shared by many single-ended logic families, which therefore cannot tolerate any signal loss much larger than about one dB.
2. Thermal or shot noise within the receiver. This difficulty is often encountered in the design of high-speed fiber- optic receivers, but not in pcb transceivers. The voltage levels used in copper -based pcb transceivers usually reside several orders of magnitude above the thermal noise floor.
3. Crosstalk from alien sources.

As you stretch the channel length to extreme distances, dispersion-limited systems do not fail due to insufficient sensitivity. They fail due to signal distortion in the form of severe deterministic jitter, also called intersymbol interference (ISI). This definition implies that at the limit of operating distance, the received data eye pattern is not open, or not open sufficiently far to permit a reasonable window of operation for the sampling circuits.

Amplifying the signal does not change the performance characteristics of a dispersion-limited system, because it is not the size of the received signal that matters, but the shape . The only fix is to adopt some form of equalization or echo cancellation. Common causes of signal distortion include

1. Bandwidth limitations within the transmitter circuit or transmitter package.
2. High-frequency losses within the communications channel.
3. Echoes and other undesirable features in the step response of the communications channel.
4. Bandwidth limitations within the receiver circuit or receiver package.

A simple chart appropriate for estimating signal loss as a function of frequency, trace geometry, and dielectric material appears in Figure 5.11. The chart applies to 50-ohm single-ended striplines and 100-ohm loosely coupled differential striplines in materials with a dielectric constant of approximately 4 at 1 GHz.

Figure 5.11. This chart estimates skin effect and dielectric losses for 50-ohm single-ended striplines and 100-ohm loosely coupled differential striplines using the approximations developed in Chapter 3.

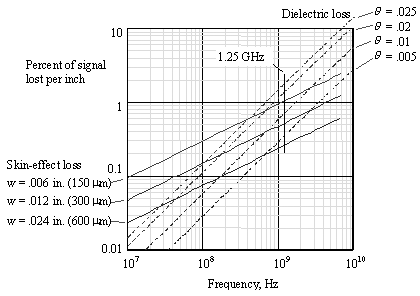
The vertical axis in the chart shows the signal lost in units of percent-signal-lost per inch. For example, the skin-effect loss for a 6-mil trace operating at a frequency of 1 GHz equals 1% of the signal amplitude for every inch traveled. The amplitude a remaining at the end of 18 inches would then be

Equation 5.14

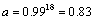
For small amounts of attenuation, you may approximate the exponential operator in [5.14] by simply adding the percentage signal lost in each inch. In the above example the approximate method estimates a signal loss of 1% per inch times 18 inches, for a total estimated loss of 18%, leaving a remaining signal amplitude of 0.82, fairly close to the value computed in [5.14]. For any percentage loss less than 25%, the correspondence between the exact method [5.14] and the simpler method of addition is better than 1 part in 20 (5% error).

To convert units of percentage-signal-lost per inch to units of dB per meter, multiply times 3.44.

Skin-effect loss curves are included for trace widths of 6, 12, and 24 mils. The trace thickness is a second-order parameter not considered in the calculation (all traces are assumed to be 1/2-oz copper striplines). The trace loss scales approximately with the inverse of trace width. Microstrips perform similarly. The same values of skin effect and dielectric loss apply equally well for 50-ohm single-ended striplines and 100-ohm loosely coupled differential striplines.

Dielectric-loss curves are included for dielectric loss tangents of 0.005, 0.01, 0.02, and 0.025. Other values of dielectric loss may be linearly interpolated on the chart from the figures shown. The skin effect and dielectric-loss effects must be summed to determine the total signal loss.

Example showing 2.5-Gb/s Serial Link

The operational characteristics of a 2.5 Gb/s link are best evaluated at a frequency of 1.25 GHz, corresponding to the maximum alternation rate for binary data operating at that speed. The loss values at this particular frequency will be highly indicative of the eye-opening loss in an actual system.

At 1.25 GHz, a 6-mil stripline trace operating on FR-4 accumulates a signal loss of roughly 1% per inch due to skin-effect loss. At an assumed dielectric loss tangent of 0.025. it accumulates another loss factor of 2% per inch due to dielectric loss. Operating at an overall distance of 8 inches, the total loss amounts to roughly 24%, a workable value provided the receiver thresholds are well centered. A modest degree of pre-emphasis would likely extend the distance at which such a link could operate .

Ordinary single-ended CMOS or bipolar TTL transceivers require that the received signal exceed V IH (or fall below V IL ) at the instant the signal is sampled. In many logic families the difference between the voltage V OH that all drivers are guaranteed to produce and the voltage V IH that all receivers are guaranteed to accept provides for a loss budget of only about 10% of the peak-to-peak signal swing. When using such a simple, unadorned transceiver, the total percentage of the signal lost, as read from Figure 5.11, must not exceed 10%. This limitation imposes a severe distance limitation on the operation of multi-gigabit data links.

The means at your disposal to improve upon any system with a sensitivity limitation include

1. Select a transceiver with a larger spread between V OH and V IH (and also between V OL and V IL ). Any improvement thus obtained in the noise margin translates directly into an increased budget for signal loss.
2. Select a transceiver with greater sensitivity. This strategy is the same as (1), just couched in analog terminology rather than in the terminology of ordinary digital logic.
3. If the system is limited by crosstalk or other interference, then reduce the interference. Determining the influence of crosstalk on sensitivity is a matter of selectively disabling adjacent channels while measuring the sensitivity of the receiver.
4. If the system is limited by self-generated noise within the receiver, then further improvements depend upon the use of a less- noisy receiver architecture, or a reduction in temperature (which tends to reduce internal thermal noise), or an increase in the transmitted signal amplitude.

Systems limited by dispersion may sometimes be improved by a change in data coding. For example, run-length limited data coding schemes that enforce DC balance produce a data spectrum with very little low-frequency content. The reception of such a coding scheme therefore depends mostly upon the spectral properties of the communications channel between some low-frequency limit (the low-frequency cutoff) and the Nyquist frequency (1/2 the data rate). To the extent that this range is smaller than the range required by ordinary binary coding (NRZ), whose spectrum extends from DC to the Nyquist frequency, the expected maximum variation in attenuation from the low-frequency limit to the Nyquist frequency is improved. Since it is the variation in attenuation across the data frequency band that determines the maximum and minimum eye height at the receiver, excising the low-frequency part of the spectrum reduces this maximum variation, resulting in a cleaner eye with less distortion. Systems limited primarily by the skin effect respond well to a change in coding because this change essentially truncates the long, lingering tail in the skin-effect step response.

In cases where the signal amplitude lies far above the thermal noise floor, but is severely distorted by AC-coupling within the communications channel, a DC-restoration circuit can completely restore the appearance of the eye. This method constitutes a type of nonlinear equalization. One type of DC-restoration circuit is discussed in the following article "SONET Data Coding."

Means of linear equalization are discussed in Section 3.14, "Linear Equalization: Long Backplane Trace Example," and in Section 8.2, "UTP Transmission Example: 10BASE-T."

POINTS TO REMEMBER

• As you stretch the channel length to extreme distances, sensitivity-limited systems fail due to insufficient signal amplitude at the receiver.
• Dispersion-limited systems fail due to signal distortion, also called intersymbol interference (ISI).
• Amplifying the received signal does not change the performance of a dispersion-limited system. Equalization is what helps.
• Systems limited by dispersion may sometimes be improved by a change in data coding.

 

5.2.1 SONET Data Coding

High Speed Digital Design Online Newsletter , Vol 5, Issue 5

Bhavesh Patel writes

I read your article on fiber-optic encoding where you explain about DC balance in different encoding schemes, and in the latter half you explain SONET data which is scrambled and how many long runs of zeros and ones it can have.

I use SONET scrambled data on my backplane. Statistically, the maximum number of 0s or 1s should be limited to 72. In my SONET framer, however, the J0/Z0 byte is not scrambled. Unless the user intentionally stuffs the J0/Z0 byte with transitions, the run length can be even higher. Even if I treat the J0/Z0 byte properly, I think a run length of 72 used with AC coupling will be a problem.

Why? Because the DC level could drift depending on the run length of zeros and ones, and this could cause eye closing at the receiver and hence increase BER. Is there a solution to this if a user has to use AC coupling? Also, does the capacitor need to be of microwave quality, which has resonance above the f knee frequency?

Reply

Thanks for your interest in High-Speed Digital Design . Regarding your inquiry, the DC balance of SONET can be terrible. If I understand your description of the coding correctly, you can get a run of 72 ones, followed by a few transitions, followed by 72 more ones, and so on. There's no good, cheap way to AC-couple such a system. Any linear circuit you try is subject to the statistical possibility that the average DC level might approach 1 (or 0) and stay there long enough to defeat your circuit. You are therefore relegated to using some form of nonlinear DC-level restoration.

Figure 5.12 shows one way to build a nonlinear DC restorer. This circuit assumes the signal has been AC-coupled at some point prior to the terminating resistor R T , stripping the signal of all low-frequency information. The purpose of the circuit is to restore the lost low-frequency components of the signal. This circuit requires that you first terminate your signal at R T and buffer it with a low-impedance linear driver.

Figure 5.12. Low-frequency information lost passing through C 1 is restored by the action of R 1 .

The circuit accomplishes two goals, behaving as both a signal filter and a feedback filter at the same time. The signal x ( t ) from the low-impedance buffer feeds through capacitor C 1 into the high-impedance input of the data slicer. From the perspective of this signal, the data slicer input appears loaded by resistance R 1 , which leads to the low-impedance output of the sampling register. The signal pathway for x ( t ) therefore comprises a high-pass filter with transfer function

 

The signal from the sampling-register output feeds through resistor R 1 into the high-impedance input of the data slicer. From the perspective of this signal, it sees the data slicer input loaded by capacitance C 1 . This pathway therefore comprises a low-pass filter with transfer function

 

The signal at the input to the slicer is the sum of the two filtered signals:

 

The clever part of this architecture is that both filters have precisely the same time constant, so the sum of the filter transfer functions H SIGNAL and H FEEDBACK is exactly unity. That's important because, if you suppose for a moment the circuit does function such that the sampling register output y ( t ) equals the input x ( t ), then the slicer input z ( t ) must also precisely equal the input x ( t ), as shown:

Assume y ( t ) = x ( t ).

 

Linearly combine the filters.

 

Recognize that the sum of these filters is a unity-gain operation.

 

Provided that y ( t ) = x ( t ), whatever low-frequency information H SIGNAL removes from x ( t ) is unerringly restored by the operation of H FEEDBACK on y ( t ).

Even if the output y ( t ) is delayed by a couple of bits, as it might be in a practical slicer circuit, the DC-restoration circuit still works as long as the amount of delay is small compared to the time constant of the low-pass filter H FEEDBACK .

This circuit makes use of two pieces of information to restore your AC-coupled signal:

1. The high-frequency content of x ( t )
2. The fact that x ( t ) is binary-valued

This circuit does not use the low-frequency content of x ( t ). That information is implied by the aforementioned two conditions. Therefore, if the low-frequency content of x ( t ) is missing, because you AC-coupled x ( t ) at some prior point in the system, the DC-restoration circuit doesn't careit still works.

As long as the time constant R 1 C 1 is shorter than the time constant of any AC-coupling network that precedes the buffer, the circuit will properly restore your signal at the input to the slicer.

This clever circuit does not require high tolerances on the AC-coupling capacitors that precede R T , nor on C 1 or R 1 . It is a very old circuit concept. It is used in (among many other modern systems) some Fast Ethernet 100 Mb/s transceivers.

I like this circuit better than systems that differentiate the incoming signal and then fire "set" and "reset" operations based upon the appearance of either positive or negative pulses in the differentiated signal. A differentiation circuit is extremely susceptible to high-frequency noise and requires multiple slicer levels. The approach in Figure 5.12 adds only a clean, low-frequency signal to your received data and therefore has almost no impact on noise performance.

POINT TO REMEMBER

• A non-linear DC restoration system can un-do the effects of AC coupling.