Hack 11. How Far? How Fast? Geo-Enabling Your Spreadsheet

How far did I go? How long did it take to get there? Calculating speeds and distances by working with geodata in Excel.

Wouldn't it be great if you could ask what-if questions of your geodata? Questions like "How far did I go on that trip?" or "What was my average speed from Tuscan to Tucumcari compared with the leg from Tehachapi to Tonopah?" A geo-enabled spreadsheet is your willing companion on this journey.

It once happened that I was trapped in a hotel with no connectivity. I had GRASS [Hack #69] on one laptop and lots of tracklogs of our wanderings through Disneyland on another laptop, and no way to get tracklogs from one computer to another. Fortunately, I had a copy of Microsoft Excel on the same computer as the tracklogs. And when all you have is a spreadsheet, then everything looks like rows and columns. As it turns out, tracklogs and waypoints naturally fit into the spreadsheet metaphor. I was able to cobble together an ugly spreadsheet analyzing our trip, but I longed for something more, dare I say, elegant?

I later learned that Jeff Laake of the National Oceanic and Atmospheric Administration faced similar challenges in his work studying marine mammals. He created a set of Visual Basic for Applications macros to add basic geospatial functions to Excel. With Jeff's library, you can turn your spreadsheet into a monster geospatial data processing engine.

I've incorporated Jeff's geofunc.xla, with minor extensions, into a sample spreadsheet with examples of the use of most of the functions. Download it at http://www.mappinghacks.com/data/spreadsheet/geodata_sample.xls. The original library, and more explanations of the functions, lives at: http://nmml.afsc.noaa.gov/Software/ExcelGeoFunctions/excelgeofunc.htm.

The first worksheet, labeled Function Examples, demonstrates the use of the library functions. My favorite function is posDist(), or position distance, which is shown in Figure 1-20. This returns the distance in nautical miles between two locations.

Figure 1-20. The posDist function in Excel

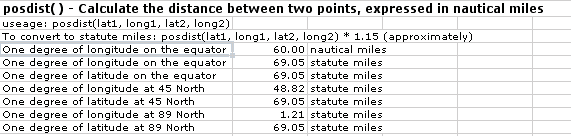
One degree of latitude or longitude at the equator should return 60 nautical miles. To convert nautical miles to statute (normal) miles, multiply nautical miles * 1.15. (To be more accurate, multiply by 6076.11549/5280, but 1.15 is less then 0.1% off.) There are about 69 statute miles per degree of latitude or longitude at the equator. The distance between degrees of latitude remain constant as you move east or west. So moving from 89 degrees to 90 degrees latitude is 69 miles. But since the lines of longitude converge at the poles, the distance between degrees of longitude decreases as you move toward the poles. The screen capture of the Function Examples worksheet shown in Figure 1-20 demonstrates this.

The posDist() function suggests possibilities! Excel has useful tools for importing and processing text files, which I use to prepare tracklogs and waypoints for further analysis. In the worksheet titled small track, you'll find a sample of a small, cleaned-up tracklog:

Lat. Long. New Seg. Flag Dist. (yards) Cum. Distance
33.81252778 -117.9163028 [1]; 
33.81255 -117.9163444 [0]; 15 15
33.81256944 -117.9161944 [0]; 46 61
33.80877222 -117.9145861 [1]; 0 61
33.80862222 -117.91465 [0]; 58 119

 

1.12.1. Importing GPS Waypoints into Your Spreadsheet

GPS waypoints and tracklogs come in a number of common formats. I used the Garnix program [Hack #49] to load my tracklogs and waypoints from my GPS. Here are the raw waypoints as returned from Garnix for the various Disneyland train stations:

33
 48' 35.98" -117
 55' 7.72" 41.0 WGS84 DTRNGATE "" [wpt_dot N]; 
33
 48' 39.50" -117
 55' 18.55" 39.0 WGS84 DTRNNEWORL "" [wpt_dot N]; 
33
 48' 53.51" -117
 55' 6.29" 54.0 WGS84 DTRNTOONTN "" [wpt_dot N]; 
33
 48' 45.45" -117
 54' 56.76" 55.0 WGS84 DTRNTOMORW "" [wpt_dot N];

Each line starts with the latitude in degrees, minutes, and seconds, followed by the longitude, altitude, datum, waypoint name, and some other irrelevant information. When I am on a trip, I like to pick a letter and start all of my waypoints with that letter. This makes it easier later to find and manage my waypoints. For this trip, the letter D seemed appropriate. So these are "Disney TRaiN" waypoints for the Gate, New Orleans Station, Toontown, and Tomorrowland.

Importing the waypoints into Excel is easy. Open the file, which causes the Text Import Wizard to launch. Select "Delimited with Space." The Text Import Wizard interprets the data as fixed width, and the defaults work just fine. However, this is a rather particular use of the word "fine," one in which the data is all present but is nearly completely unusable! The waypoints are in the sheet named Disney Waypoints within geodata_sample.xls, as shown in Figure 1-21.

Figure 1-21. Raw waypoints, before processing with SplitMinSecToDeg( ) function

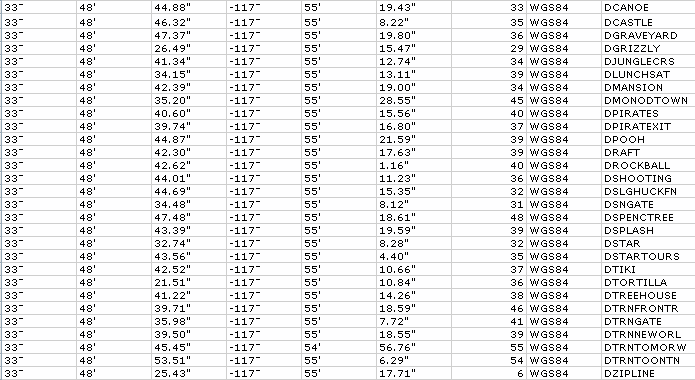
Degrees, minutes, and seconds of both latitude and longitude are split into their own cells, and there are degree, minute, and second marks that cause Excel to treat the numbers as strings. We need to rid ourselves of these vexatious non-numbers and then convert the degree-minute-second (DMS) notation to decimal degree form [Hack #25] .

In the absence of Perl, whose technology for manipulating this sort of data is so advanced as to be indistinguishable from magic, we need a bit of Excel function hackery. I've added a copy of the Deg/Min/Sec columns for both latitude and longitude next to the original import and then inserted a set of nested functions to strip the degree, minute, and second marks and cause Excel to treat the values as numbers.

The SplitMinSecToDeg() function takes care of stripping off the special character. The minute (') and second (") characters are easy, but I find it easiest to copy the degree symbol and paste it into the formula. Note that I've created named ranges for each column to make this easier to read:

=LEFT(lat_deg,FIND("
",lat_deg)-1)+0
=LEFT(lat_min,FIND("'",lat_min)-1)+0
=LEFT(lat_sec,FIND("""",lat_sec)-1)+0
=LEFT(long_deg,FIND("
",long_deg)-1)+0
=LEFT(long_min,FIND("'",long_min)-1)+0
=LEFT(long_sec,FIND("""",long_sec)-1)+0

The geofunc.vba package includes the function SplitMinSecToDeg(), which takes degrees, minutes, and seconds that are split into columns and combines them to create decimal degrees. The results are stored in columns A and B:

=SplitMinSecToDeg(P11,Q11,R11)

There is a trick to SplitMinSecToDeg() that comes up when you try to do the equivalent function manually. You should be able to convert from DMS to decimal degrees with this formula:

=deg_clean+min_clean/60+sec_clean/3600

But wait! That shows the original longitude as being -117 55' 8.44", while the formula then comes up with -116.08099. What is going on? This is a consequence of using positive and negative numbers to depict latitudes north and south of the equator and longitudes east and west of the prime meridian. The problem is that Disneyland is not at negative 117 degrees of longitude; it is at positive 117 degrees west of the prime meridian. There are many ways to abuse math in Excel, but here is one fix:

=SIGN(S11)*(ABS(S11)+T11/60+U11/3600)

After this correction, we have the right latitude and longitude! The correction should also be done on latitude, except that because Disneyland is in California, I need not worry about the Southern Hemisphere in this particular example.

I like to develop spreadsheets one step at a time, rather then creating one monstrous, impossible-to-understand formula. Since there is also something to be said for the all-in-one approach, here are the same formulas rolled together at once, which are stored in the sheet labeled Disney Waypoints-all in one:

=SplitMinSecToDeg(LEFT(D11,FIND("¬",D11)-1)+0,LEFT(E11,FIND("'",E11)-1)+0,
LEFT(F11,FIND("""",F11)-1)+0)=SplitMinSecToDeg(LEFT(G11,FIND("¬",G11)-1)+0,
LEFT(H11,FIND("'",H11)-1)+0,LEFT(I11,FIND("""",I11)-1)+0)

This sheet also uses the posDist() function to calculate the distance between successive waypoints. This sets the stage for [Hack #12] .

1.12.2. Importing GPS Tracklogs into Your Spreadsheet

Importing a GPS tracklog follows the same model as importing the waypoints. A Garnix format tracklog looks like this:

33
 48' 30.58" -117
 54' 48.88" 35.0 WGS84 01:21:45-2004/03/14 [1];
33
 48' 30.89" -117
 54' 53.44" 35.0 WGS84 01:23:26-2004/03/14 [1];
33
 48' 30.89" -117
 54' 54.60" 30.0 WGS84 01:23:40-2004/03/14 [0];
33
 48' 30.89" -117
 54' 54.60" 39.0 WGS84 01:23:46-2004/03/14 [0];

Each line contains latitude, longitude, altitude (if supported by your GPS unit), datum, timestamp, and new-segment flag. The new-segment flag is set when that track point represents the start of a new segment either because the GPS was turned off, or too much time has passed. In [Hack #71], we'll see what happens when you treat all track points as part of the same line. The center cannot hold, and random straight lines blur the clarity of the trip!

The sheet Disney Track shows a sample tracklog that has been imported into Excel and processed to a clean display of lat/long (Figure 1-22).

Figure 1-22. Track log with distance, time, and speed

 

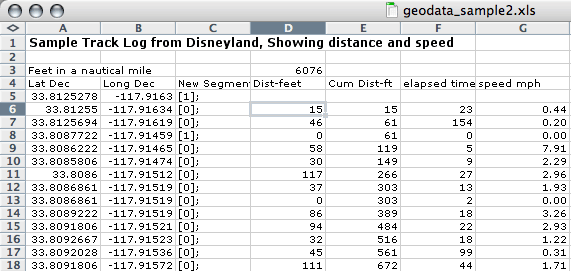
1.12.3. Calculating Cumulative Distance and Speed

With latitude, longitude, and the new-segment flag in columns A, B, and C, we can calculate distance. We must first look at the new-segment flag. If this is a new segment, indicated by [1];, then we should skip calculating the distance. Otherwise the distance in feet is given with the posDist() function multiplied by the number of feet in a nautical mile.

=IF(C6="[0];", posdist(A5,B5,A6,B6)*$D$3,0)

And the cumulative trip distance:

=SUM($D$5:D6)

The Garnix datestamp is well suited for Excel. You can subtract the timestamp of the previous track point from the current timestamp to get the elapsed time. To make it more interesting, you need to check the new-segment flag and ignore the time between segments (unless you are calculating a time stopped). You also need to multiply the elapsed time by the number of seconds in one day in order to get the elapsed time in seconds. Assuming the following timestamps are in cells P5 and P6, then:

3/13/2004 5:44:30 AM
3/13/2004 5:44:53 AM
 
=IF(C6="[0];", (P6-P5)*86400,0)

which equals 23 seconds elapsed time.

In those 23 seconds we went 15 feet. So to calculate the speed in miles per hour, we need to convert 23 seconds to hours, and 15 feet to miles.

This checks that the elapsed time is not zero and then converts feet in D6 to miles, and seconds in cell F6 to hours:

=IF(F6<>0,(D6/5280)/(F6/3600),0)

So 15 feet in 23 seconds is about 0.44 mph. Way down in row 104, we went 43.43 mph. Quite the thrill park! (Hey, when riding with a five and six year old, 43.43 mph is pretty darn fast!)

1.12.4. Geo-Enabling Other Spreadsheets

Once you have played with the sample sheet, you'll want to install the macros as a plug-in, so you can use the geospatial functions in your own spreadsheets. You can get a copy of the VBA functions from http://www.mappinghacks.com/data/spreadsheet/geofunc.xla.

Download the file and place it in Excel, select Tools images/ent/U2192.GIF border=0> Add-ins, and click Select. Navigate to your download directory, select the file geofunc.xla, and click Open. Congratulations, you now have a geo-enabled spreadsheet!

The original version of the geofunc.xla library lives at http://nmml.afsc.noaa.gov/Software/ExcelGeoFunctions/excelgeofunc.htm. There is also more information about the original functions in the library at that site.

Loading geodata into a spreadsheet extends the great tools we are accustomed to in numerical analysis to the problems of acquisition, management, and presentation of information with a geospatial component.