SUMMARIZATION

One of the predominant operations on multidimensional aggregate data is that "to remove" a dimension from a multidimensional aggregate data (obtaining, for example, a "Population by year and age-groups" from a "Population by year, age-groups, and sex"). Such an operation is often called summarization. This operator works with only one operand, and it produces a recomputed measure (in the case of numerical values) or instances formed by sets of alphanumeric values (in the case of non-numerical values). The first formal proposal of summarizing an attribute, reducing the number of dimensions of a MAD (in that case, a table), was made in Rafanelli & Ricci (1984, 1985), and subsequently in Fortunato et al. (1986), Rafanelli & Shoshani (1990), and Rafanelli & Ricci (1993). In Gyssens & Lakshamanan (1997), the authors study this operator both on relations, and on tables.

Other different terms have been used for this operation. Among them, we remember aggregation, informally discussed in Shoshani & Wong (1985), where, among the different concepts discussed, there is that of the "collapsing" of multidimensional data structures in order to remove a certain dimension; attribute removal by aggregation in Ozsoyoglu, Ozsoyoglu, & Mata (1985), slice (term especially used for OLAP applications) in Gyssens & Lakshamanan (1997) and in Shoshani (1997), and destroy dimension in Agraval, Gupta, & Sarawagi (1997). Since the term "aggregation" has been widely used in this chapter to denote a different concept, in the following we will use the terms summarization (which often refers to the statistical databases) and removing with the same meaning. Often, when referring to the relational algebra, this operator is called projection, as in Ozsoyoglu, Ozsoyoglu, & Matos (1987), Pedersen & Jensen (1999), and Pedersen, Jensen, & Dyreson (2001), with very few differences.

As already mentioned, this operator deletes one category attribute of a MAD, with consequent recomputation of the summary attribute values. This recomputation is not always possible: for example, if the measure is not numeric, or if, in the case of numeric values, the summary type of the MAD is "average." In this latter case we need the relative "count" and "sum" aggregate summary values, or the raw data, to which to apply the aggregation process again. Since a multidimensional aggregate data structure represents a functional link between sets of raw data (rather than n-tuples of dimension instances) and measures, in our framework summarization is the operation that allows the user to (implicitly or explicitly) delete one attribute (which, in this case, represents one dimension of the MAD), or to transform it into an implicit one, and to recompute the measures accordingly.

In the following, in order to avoid ambiguity, we will distinguish the total summarization or T-SUMMARIZATION (which implies the removal of the dimension) from the implicit summarization or I-SUMMARIZATION (which transforms the dimension from explicit to implicit, and the set of definition domain instances in only one set-value, which resume all the values of the original domain, but not all the values of the primitive attribute definition domain). The descriptive space of the MAD reduces itself to one dimension without loss of information only in the first case.

In Bezenchek, Rafanelli, & Tininini (1996a) and, subsequently, in the ADAMO model (see Bezenchek, Rafanelli, & Tininini, 1996b) in Chapter 1, the above-mentioned distinction between total summarization and implicit summarization was made. Therefore, with the introduction of the "implicit attribute" concept, the summarization operator has been refined. The (total or implicit) summarizability of a category attribute, or its non-summarizability, depends on three interdependent factors, namely:

1. the partitioning characteristics of the category attribute

2. the fact described by the MAD;

3. the aggregation function type applied to the raw data to obtain this MAD.

In particular, it has been shown that the partitioning characteristics of depend on itself and on the specified instances, but also on the particular fact described by the MAD. For example, the attribute continents, with its instances Africa, America, Asia, Europe, and Oceania, partitions the fact domain corresponding to "population" but does not partition (since it does not cover) the fact domain corresponding to "terrestrial surface." In principle, the system can automatically determine whether a given attribute in a MAD a is (T- or I-) summarizable, provided that it has an adequate knowledge regarding the instances of the category attribute combined with the specified fact and aggregation function type. However, this is not always true in practice, and the summarizability of a category attribute also depends on the particular survey which has produced the MAD, i.e., on a collection of metadata, which has to be produced together with the aggregate data themselves. Note that, when speaking of dimension, in general we intend one level (i.e., one category attribute) of one of the possible hierarchies in a dimension; for the sake of simplicity, when ambiguities are not possible, we will call it dimension, collapsing the more complex meaning of the term into the simpler term of a descriptive variable.

For example, let us consider the MAD "Number_of_ cars_produced_in_Japan" in Figure 10, described by "model" and "years" (but also by "country," where this dimension is "implicit" because it has only one value, "Japan," which appears in the title of the MAD). Suppose we wish to have the total number of cars produced only per "years." In this case we have to apply the summarization operation to the category attribute "model." Because the instances of the category attribute model are <Corolla, Civic, Corona>, and because these are not the only car models produced in Japan in that period, the operator applied will be I-SUMMARIZATION. In this way the category attribute "model" will be transformed into an implicit attribute and a note will be added to the MAD, as shown in Figure 11.

Figure 10

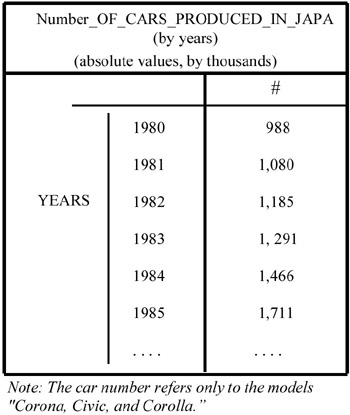
Figure 11

We remember that in the Chapter 1 we gave the formal definition of a simple MAD s₁. Therefore, given a phenomenon x and given the set of all the relations R_x (of the micro database) involved in the production of all the MAD which describe this phenomenon, we considered the subset of R_x formed only by the relations involved in the building of fact . As illustrated in Chapter 1, we call this subset an aggregation relation, and denote it by R₁^x, where The base relation of s₁ (that is, the descriptive space which describes fact ) is the subset of the aggregation relation of this fact which has all and only the descriptive attributes A_B1j (with j = 1, …, s) of the fact

Let us suppose the summarizability conditions, discussed in the previous Chapter 4, have been verified. Then s₁ is a MAD defined on the base relation (subset of the aggregation relation R₁^x which refers to fact, where ). Therefore, its descriptive space is the base relation B1 mentioned above, has its components formed by the set {A_1j}, with j = 1, …, s, where s is the number of category attributes (cardinality) of MAD s₁. Let be the six-tuple which defines s₁. Let be formed by e₁ = {E₁, E₂, …, E_M}, i.e., the set of its explicit category attributes, each of them with its corresponding ordered instance domain with M ≤ s, and by i1, i.e., the set of its implicit category attributes.

The summarization of s₁ with respect to A1x (with x ∊ {1, …, M}) produces a new MAD

where N, are the same and P' is the new name of the MAD; and s' is a set of recomputed summary values. This recomputation depends on the type of aggregation function (e.g., count, sum, average) applied to the original microdata.

A_1x becomes an implicit category attribute of s'₁. It can completely disappear from the new descriptive space {A_1'j'}, with j' = 1, …, x−1, x+1, …, s, if its definition domain Δ (Ex) completely covers the definition domain of the unique top-level category attribute (denoted by ALL, see Gray et al., 1997) of the hierarchy to which it belongs. If, instead, A_1x does not belong to any hierarchy, it disappears only if its definition domain coincides with its primitive definition domain.