Example Problem Solution

[Page 145 ( continued )]

As a prelude to the problems, this section presents an example solution of the formulation and computer solution of a linear programming problem.

Problem Statement

Bark's Pet Food Company produces canned cat food called Meow Chow and canned dog food called Bow Chow. The company produces the pet food from horse meat, ground fish, and a cereal additive. Each week the company has 600 pounds of horse meat, 800 pounds of ground fish, and 1,000 pounds of cereal additive available to produce both kinds of pet food. Meow Chow must be at least half fish, and Bow Chow must be at least half horse meat. The company has 2,250 16-ounce cans available each week. A can of Meow Chow earns $0.80 in profit, and a can of Bow Chow earns $0.96 in profit. The company wants to know how many cans of Meow Chow and Bow Chow to produce each week in order to maximize profit.

1. Formulate a linear programming model for this problem.

2. Solve the model by using the computer

Solution

A. Model Formulation

Step  1.	Define the Decision Variables This problem encompasses six decision variables, representing the amount of each ingredient i in pet food j : x ij = ounces of ingredient i in pet food j per week, where i = h (horse meat), f (fish), and c (cereal), and j = m (Meow Chow) and b (Bow Chow) [Page 146] To determine the number of cans of each pet food produced per week, the total ounces of Meow Chow produced, x hm + x fm + x cm , and the total amount of Bow Chow produced, x hb + x fb + x cb , would each be divided by 16 ounces.
Step  2.	Formulate the Objective Function The objective function is to maximize the total profit earned each week, which is determined by multiplying the number of cans of each pet food produced by the profit per can. However, because the decision variables are defined in terms of ounces, they must be converted to equivalent cans by dividing by 16 ounces, as follows : or maximize Z = $0.05( x hm + x fm + x cm ) + 0.06( x hb + x fb + x cb )
Step  3.	Formulate the Model Constraints The first set of constraints represents the amount of each ingredient available each week. The problem provides these in terms of pounds of horse meat, fish, and cereal additives . Thus, because the decision variables are expressed as ounces, the ingredient amounts must be converted to ounces by multiplying each pound by 16 ounces. This results in these three constraints: x hm + x hb 9,600 oz. of horse meat x fm + x fb 12,800 oz. of fish x cm + x cb 16,000 oz. of cereal additive Next, there are two recipe requirements specifying that at least half of Meow Chow be fish and at least half of Bow Chow be horse meat. The requirement for Meow Chow is formulated as or - x hm + x fm - x cm The constraint for Bow Chow is developed similarly: or x hb x fb x cb Finally, the problem indicates that the company has 2,250 16-ounce cans available each week. These cans must also be converted to ounces to conform to our decision variables, which results in the following constraint: x hm + x fm + x cm + x hb + x fb + x cb 36,000 oz.
Step  4.	The Model Summary The complete model is summarized as [Page 147] x hb x fb x cb x hm + x fm + x cm + x hb + x fb + x cb 36,000 x ij B. Computer Solution 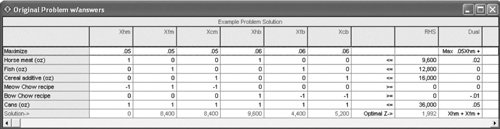The computer solution for this model was generated by using the QM for Windows computer software package. The solution is x hm = 0 x fm = 8,400 x cm = 8,400 x hb = 9,600 x fb = 4,400 x cb = 5,200 Z = $1,992 To determine the number of cans of each pet food, we must sum the ingredient amounts for each pet food and divide by 16 ounces (the size of a can): x hm + x fm + x cm = 0 + 8,400 + 8,400 = 16,800 oz. of Meow Chow or or 19,200 · 16 = 1,200 cans of Bow Chow Note that this model has multiple optimal solutions. An alternate optimal solution is x fm = 10,400, x cm = 6,400, x hb = 9,600, and x cb = 9,600. This converts to the same number of cans of each pet food; however, the ingredient mix per can is different.