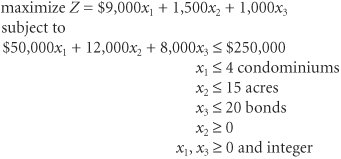Integer Programming Models
| There are three basic types of integer linear programming modelsa total integer model, a 01 integer model, and a mixed integer model. In a total integer model , all the decision variables are required to have integer solution values. In a 01 integer model , all the decision variables have integer values of zero or one. Finally, in a mixed integer model , some of the decision variables (but not all) are required to have integer solutions. The following three examples demonstrate each of these types of integer programming models. The three types of integer programming models are total, 01, and mixed. A Total Integer Model ExampleThe owner of a machine shop is planning to expand by purchasing some new machinespresses and lathes. The owner has estimated that each press purchased will increase profit by $100 per day and each lathe will increase profit by $150 daily. The number of machines the owner can purchase is limited by the cost of the machines and the available floor space in the shop. The machine purchase prices and space requirements are as follows :
In a total integer model , all decision variables have integer solution values . The owner has a budget of $40,000 for purchasing machines and 200 square feet of available floor space. The owner wants to know how many of each type of machine to purchase to maximize the daily increase in profit. The linear programming model for an integer programming problem is formulated in exactly the same way as the linear programming examples in Chapters 2, 3, and 4. The only difference is that in this problem, the decision variables are restricted to integer values because the owner cannot purchase a fraction, or portion, of a machine. The linear programming model follows: The decision variables in this model are restricted to whole machines. The fact that both decision variables, x 1 and x 2 , can assume any integer value greater than or equal to zero is what gives this model its designation as a total integer model. A 01 Integer Model ExampleA community council must decide which recreation facilities to construct in its community. Four new recreation facilities have been proposeda swimming pool, a tennis center, an athletic field, and a gymnasium. The council wants to construct facilities that will maximize the expected daily usage by the residents of the community, subject to land and cost limitations. The expected daily usage and cost and land requirements for each facility follow:
In a 01 integer model , the solution values of the decision variables are zero or one . The community has a $120,000 construction budget and 12 acres of land. Because the swimming pool and tennis center must be built on the same part of the land parcel , however, only one of these two facilities can be constructed . The council wants to know which of the recreation facilities to construct to maximize the expected daily usage. The model for this problem is formulated as follows: where x 1 = construction of a swimming pool x 2 = construction of a tennis center x 3 = construction of an athletic field x 4 = construction of a gymnasium In this model, the decision variables can have a solution value of either zero or one . If a facility is not selected for construction, the decision variable representing it will have a value of zero. If a facility is selected, its decision variable will have a value of one. The last constraint, x 1 + x 2 If the community had specified that either the swimming pool ( x 1 ) or the tennis center ( x 2 ) must be built, but not both, then the last constraint would become an equation, x 1 + x 2 = 1. This would result in a solution that would include x 1 = 1 or x 2 = 1, but both would not equal one (nor would both equal zero). In this manner, the model forces a choice between the two facilities. For this reason, it is often called a multiple-choice constraint . A variation of the multiple-choice constraint can be used to formulate a situation where some specific number of facilities out of the total must be constructed. For example, if the community council had specified that exactly two of the four facilities must be built, this constraint would be formulated as x 1 + x 2 + x 3 + x 4 = 2 If, alternatively, the council had specified that no more than two facilities must be constructed, the constraint would be x 1 + x 2 + x 3 + x 4 Another type of 01 model constraint is a conditional constraint . In a conditional constraint, the construction of one facility would be conditional upon the construction of another. Suppose, for example, that the pet project of the head of the community council is the swimming pool, and she also believes the tennis center is frivolous. The council head is very influential, so the rest of the council knows that the tennis center has no chance of being selected if the pool is not selected first. However, even if the pool is selected, there is no guarantee that the tennis center will also be selected. Thus, the tennis center ( x 2 ) is conditional upon construction of the swimming pool ( x 1 ). This condition is formulated as x 2 Notice that the tennis center ( x 2 ) cannot equal one (i.e., be selected) unless the pool ( x 1 ) equals one. If the pool ( x 1 ) equals zero (i.e., it is not selected), then the tennis center ( x 2 ) must also equal zero. However, this condition does allow the pool ( x 1 ) to equal one and be selected and the tennis center to equal zero and not be selected. A variation of this type of conditional constraint is the corequisite constraint , wherein if one facility is constructed, the other one would also be constructed and vice versa. For example, suppose the council worked out a political deal among themselves , wherein if the pool is accepted, the tennis center must also be selected and vice versa. This constraint is written as x 2 = x 1 This constraint makes x 1 and x 2 equal the same value, either zero or one. A Mixed Integer Model ExampleNancy Smith has $250,000 to invest in three alternative investmentscondominiums, land, and municipal bonds . She wants to invest in the alternatives that will result in the greatest return on investment after 1 year. In a mixed integer model , some solution values for decision variables are integers and others can be nonintegers . Each condominium costs $50,000 and will return a profit of $9,000 if sold at the end of 1 year; each acre of land costs $12,000 and will return a profit of $1,500 at the end of 1 year; and each municipal bond costs $8,000 and will result in a return of $1,000 if sold at the end of 1 year. In addition, there are only 4 condominiums, 15 acres of land, and 20 municipal bonds available for purchase. The linear programming model for this problem is formulated as follows: where x 1 = condominiums purchased x 2 = acres of land purchased x 3 = bonds purchased
Notice that in this model the solution values for condominiums ( x 1 ) and municipal bonds ( x 3 ) must be integers. It is not possible to invest in a fraction of a condominium or to purchase part of a bond. However, it is possible to purchase less than an acre of land (i.e., a portion of an acre). Thus, two of the decision variables ( x 1 and x 3 ) are restricted to integer values, whereas the other variable ( x 4 ) can take on any real value greater than or equal to zero. |
EAN: 2147483647
Pages: 358
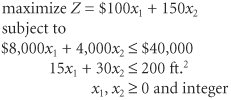
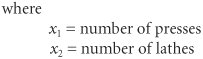
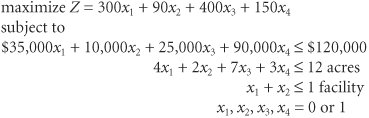
 1, reflects the
1, reflects the