Integer Programming Graphical Solution
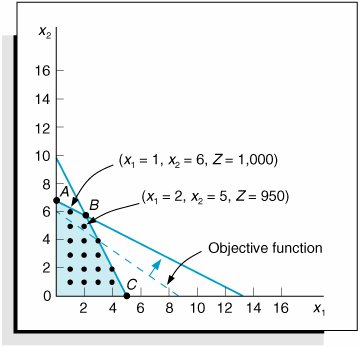
| It may seem logical that an easy way to solve integer programming problems is to round off fractional solution values to integer values. However, that can result in less than optimal (i.e., suboptimal ) results. This outcome can be seen by using graphical analysis. As an example, consider the total integer model for the machine shop formulated in the previous section: First, we will use Excel to solve this model as a regular linear programming model without the integer requirements, as shown in Exhibit 5.1 Exhibit 5.1.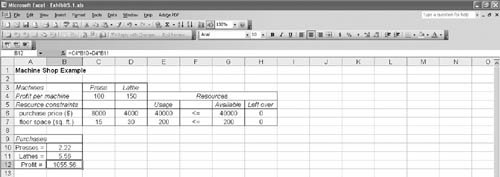 Notice that this model results in a noninteger solution of 2.22 presses and 5.56 lathes, or x 1 = 2.22 and x 2 = 5.56. Because the solution values must be integers, let us first round off these two values to the closest integer values , which would be x 1 = 2 and x 2 = 6. However, if we substitute these values into the second model constraint, we find that this integer solution violates the constraint and thus is infeasible: Rounding noninteger solution values up to the nearest integer value can result in an infeasible solution . In a model in which the constraints are all A feasible solution is ensured by rounding down noninteger solution values . However, one of the difficulties of simply rounding down non-integer values is that another integer solution may result in a higher profit (i.e., in this problem, there may be an integer solution that will result in a profit higher than $950). In order to determine whether a better integer solution exists, let us analyze the graph of this model, which is shown in Figure 5.1. Figure 5.1. Feasible solution space with integer solution points In Figure 5.1 the dots indicate integer solution points, and the point x 1 = 2, x 2 = 5 is the rounded-down solution. Notice that as the objective function edge moves outward through the feasible solution space, there is an integer solution point that yields a greater profit than the rounded-down solution. This solution point is x 1 = 1, x 2 = 6. At this point, Z = $1,000, which is $50 more profit per day for the machine shop than is realized by the rounded-down integer solution. A rounded-down integer solution can result in a less than optimal (suboptimal) solution . This graphical analysis explicitly demonstrates the error that can result from solving an integer programming problem by simply rounding down. In the machine shop example, the optimal integer solution is x 1 = 1, x 2 = 6, instead of the rounded-down solution, x 1 = 2, x 2 = 5 (which is often called the suboptimal solution or result). Because erroneous results are caused by rounding down regular solutions, a more direct approach for solving integer problems is required. The traditional approach for solving integer programming problems is the branch and bound method . It is a mathematical solution approach that can be applied to a number of different types of problems. The branch and bound method is based on the principle that the total set of feasible solutions (such as the feasible area in Figure 5.1) can be partitioned into smaller subsets of solutions. These smaller subsets can then be evaluated systematically until the best solution is found. The branch and bound method is a tedious and often complex mathematical process. Fortunately, both Excel and QM for Windows have the capability to solve integer programming problems, and thus we will rely on the computer to solve the different types of integer models demonstrated in this chapter. However, for the interested reader, the CD that accompanies this text includes a supplementary module, "Integer Programming: The Branch and Bound Method," that demonstrates the branch and bound method in detail. |
EAN: 2147483647
Pages: 358
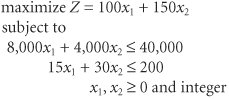
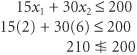
 (and the constraint coefficients are positive), a feasible solution is always ensured by
(and the constraint coefficients are positive), a feasible solution is always ensured by