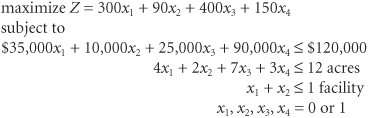[Page 187]
Computer Solution of Integer Programming Problems with Excel and QM for Windows
Integer programming problems can be
solved
using Excel spreadsheets and QM for Windows. In this section we
demonstrate
both of these computer solution approaches, using the examples for 01, total, and mixed integer programming problems developed in the previous sections.
Solution of the 01 Model with Excel
Recall our
recreational
facilities example, formulated on page 182:
where
x
1
= construction of a swimming pool
x
2
= construction of a tennis center
x
3
= construction of an athletic field
x
4
= construction of a gymnasium
Z
= total expected usage (people) per day
Exhibit 5.2 shows this example model set up in Excel spreadsheet format. The decision
variables
for the facilities are in
cells
C12:C15
, and the objective function (
Z
) is embedded in cell C16. The objective function is shown on the formula bar at the top of the spreadsheet. The model constraints are contained in cells G7, G8, and G9. For example,
cell
G7 includes the cost constraint, =
C7
*
C12+D7
*
C13+E7
*
C14+F7
*
C15
, and the available budget of $120,000 is contained in cell I7. Thus, the cost constraint will be written in Solver as
G7
I7
.
Exhibit 5.2.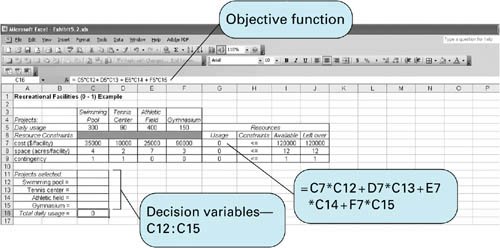
Exhibit 5.3 shows the Solver screen for our spreadsheet example. Notice that we have established the 01 condition of our variables by constraining the decision variable cells to be less than or equal to one (i.e.,
C12:C15
1
).
[Page 188]
Exhibit 5.3.
Time Out: For Ralph E. Gomory
In 1958 Ralph Gomory was the first individual to develop a systematic (algorithmic) approach for solving linear integer programming problems. His "cutting plane method" is an algebraic approach based on the systematic addition of new constraints (or cuts), which are satisfied by an integer solution but not by a continuous variable solution. An alternative to an algebraic approach like Gomory's is an enumerative approach, which is a means of searching through all possible integer solutions (but in an
intelligent
manner) to limit the extent of the search. One such search method is the branch and bound technique, introduced in 1960 by A. H. Land and A. C. Doig of the London School of Economics and Political Science.
|
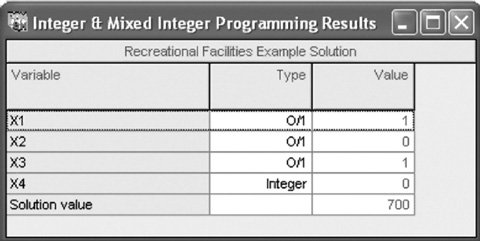
Next, we constrain the decision variables to be integer (i.e.,
C12:C15=integer
). The addition of this latter constraint is shown in Exhibit 5.4. These two constraints, along with the nonnegativity constraint (
C12:C15
), establish a condition wherein if the decision variables are nonnegative, less than or equal to one, and integer, then they must be zero or one. The remaining constraints are the same as you would have for a normal linear programming model. The spreadsheet solution to our example is obtained by clicking on the "Solve" button in the Solver window and is shown in Exhibit 5.5.
Exhibit 5.4.
Exhibit 5.5.
(This item is displayed on page 189 in the print version)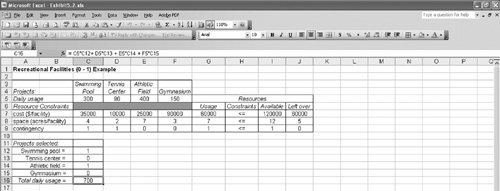
Solution of the 01 Model with QM for Windows
The 01 integer programming problem is solved in the "Integer and Mixed Integer" module of QM for Windows. We will demonstrate this module by using our example for selecting recreational facilities that we just solved with Excel.
[Page 189]
Exhibit 5.6 shows the data input screen for our recreational facilities example problem. At the bottom of the screen, when you click on "Variable Type" for a variable, a menu will be displayed from which you can
indicate
if the variable is 01, integer, or real. In the case of this example, all the variables should be designated 01. The model is solved by clicking on the "Solve" button at the top of this screen, which results in the solution screen shown in Exhibit 5.7.
Exhibit 5.6.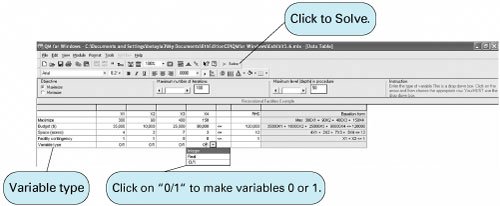
Exhibit 5.7.
[Page 190]
Management Science Application: College of Business Class Scheduling at Ohio University
The College of Business at Ohio University in Athens, Ohio, encompasses four academic departmentsAccounting, Finance, Management Information Systems, and Marketingwith approximately 65 to 75 instructors. Each academic
term
, the college departments offer 110 to 130 sections of different courses. The college's home building is Copeland Hall, which includes 14 to 16 classrooms. Prior to 1998 the college used a manual process to schedule courses and instructors into classrooms at different times during the day. An associate dean would allocate the classrooms to the different departments, and the department
chair
would assign courses to instructors and schedule the course sections to the rooms, sometimes taking into account instructor preferences. If a chairperson did not use all of the department's allocated classrooms, they were shared with other departments, and if a department's available classrooms were not sufficient to accommodate all its courses, they were assigned to classrooms outside the building.
While this process was
workable
, it was not optimal; and instructors' preferences weren't often
considered
, and they often taught outside the building because course sections couldn't be matched with classrooms of sufficient
size
. For example, instructors might have wished to only teach certain courses at certain times and on certain days, and they might have wanted to avoid back-to-back classes.
Since 1998 the college has used an integer programming model to develop course schedules. The model
assigns
instructors to courses in classrooms during specific time slots, based on instructor preference forms developed within the departments. The typical integer programming model for course scheduling in a semester includes more than 2,500 variables and almost 2,000 constraints. The model has improved the use of classroom space, instructors have to teach fewer courses outside Copeland Hall (despite increasing enrollments), instructors are more satisfied with their schedules, and the time to develop schedules has been cut in half.
Source: C. H. Martin, "Ohio University's College of Business Uses Integer Programming to Schedule Classes,"
Interfaces
34, no. 6 (NovemberDecember 2004): 460465.
|
{% if main.adsdop %}{% include 'adsenceinline.tpl' %}{% endif %}
The solution shown in the QM for Windows output is
x
1
= 1 swimming pool
x
2
= 0 tennis center
x
3
= 1 athletic field
x
4
= 0 gymnasium
Z
= 700 people per day expected usage
Solution of the Total Integer Model with Excel
We will demonstrate the Excel solution of a total integer programming problem for the machine shop example we solved previously using the branch and bound method. Recall that this model was formulated as
[Page 191]
where
x
1
= number of presses
x
2
= number of lathes
The machine shop example set up in spreadsheet format is shown in Exhibit 5.8. This is the same basic format as a linear programming model. The essential difference between solving a regular linear programming model and an integer programming model is that we must
designate
the cells representing the decision variables as being "integer." We accomplish this by adding a constraint within Solver that establishes
B10:B11
as integers, as shown in Exhibit 5.10. The complete Solver, with all constraints, is shown in Exhibit 5.9. Clicking on the "Solve" button will generate the spreadsheet solution, as shown in Exhibit 5.11.
Exhibit 5.8.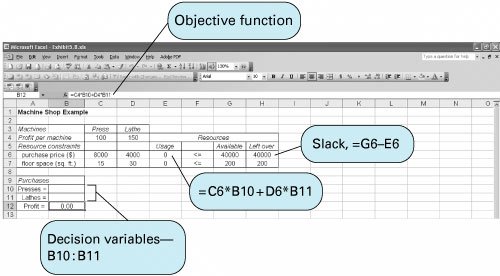
Exhibit 5.9.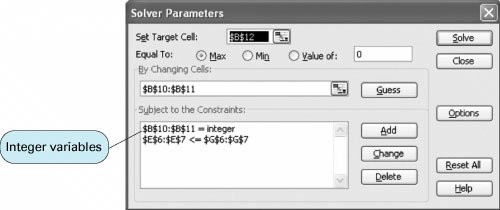
[Page 192]
Exhibit 5.10.
Exhibit 5.11.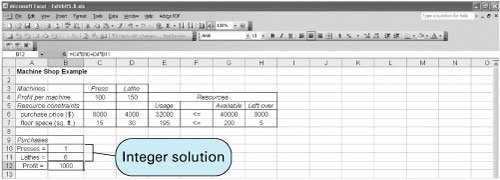
Solution of the Mixed Integer Model with Excel
The solution of a mixed integer programming model with Excel will be demonstrated by using the example for investments formulated earlier in the chapter:
where
x
1
= condominiums purchased
x
2
= acres of land purchased
x
3
=
bonds
purchased
The Excel spreadsheet solution is shown in Exhibit 5.12, and the Solver window is shown in Exhibit 5.13. The decision variables are contained in cells
B8:B10
. The objective function formula is in cell B11 and is also displayed on the formula bar at the top of the spreadsheet. Notice that we did not include the constraint values for the availability of each type of investment (i.e., 4 condos, 15 acres of land, and 20 bonds) in the spreadsheet setup. Instead, it was easier just to enter these constraints directly into Solver, as shown in Exhibit 5.13. Notice in Solver that we have designated B8 and B10 as integers, but we have not designated B9 as an integer, reflecting the fact that
x
1
and
x
3
are integers, whereas
x
2
is a real variable.
[Page 193]
Exhibit 5.12.
Exhibit 5.13.
Solution of the Mixed Integer Model with QM for Windows
The "Integer and Mixed Integer" module of QM for Windows is used to solve our investment example. When the problem data are input, we must designate the variable types for each decision variable. In this case,
x
1
and
x
3
are entered as integer variables, and
x
2
is entered as a real variable. The QM for Windows input screen for our investment example is shown in Exhibit 5.14, and the solution screen is shown in Exhibit 5.15.
Exhibit 5.14.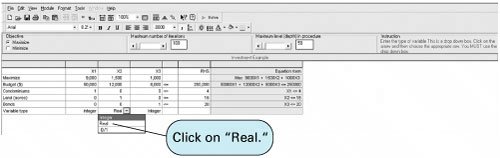
[Page 194]
Exhibit 5.15.
|
