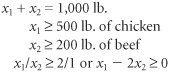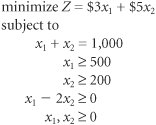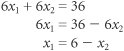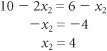Example Problem Solutions

[Page 57 ( continued )]

As a prelude to the problems, this section presents example solutions to two linear programming problems.

Problem Statement

Moore's Meatpacking Company produces a hot dog mixture in 1,000-pound batches. The mixture contains two ingredientschicken and beef. The cost per pound of each of these ingredients is as follows :

Ingredient	Cost/lb.
Chicken	$3
Beef	$5

---

[Page 58]

Each batch has the following recipe requirements:

1. At least 500 pounds of chicken

2. At least 200 pounds of beef

The ratio of chicken to beef must be at least 2 to 1. The company wants to know the optimal mixture of ingredients that will minimize cost. Formulate a linear programming model for this problem.

Solution

Step  1.	Identify Decision Variables Recall that the problem should not be "swallowed whole." Identify each part of the model separately, starting with the decision variables: x 1 = lb. of chicken x 2 = lb. of beef
Step  2.	Formulate the Objective Function
Step  3.	Establish Model Constraints The constraints of this problem are embodied in the recipe restrictions and (not to be overlooked) the fact that each batch must consist of 1,000 pounds of mixture: and x 1 , x 2 The Model

Problem Statement

Solve the following linear programming model graphically:

---

[Page 59]

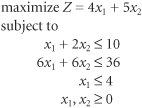
Solution

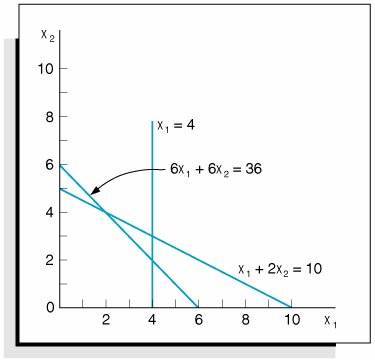
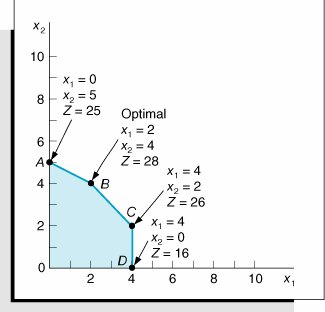
Step  1.	Plot the Constraint Lines as Equations A simple method for plotting constraint lines is to set one of the constraint variables equal to zero and solve for the other variable to establish a point on one of the axes. The three constraint lines are graphed in the following figure: The constraint equations
Step  2.	Determine the Feasible Solution Area The feasible solution area is determined by identifying the space that jointly satisfies the conditions of all three constraints, as shown in the following figure: The feasible solution space and extreme points
Step  3.	Determine the Solution Points The solution at point A can be determined by noting that the constraint line intersects the x 2 axis at 5; thus, x 2 = 5, x 1 = 0, and Z = 25. The solution at point D on the other axis can be determined similarly; the constraint intersects the axis at x 1 = 4, x 2 = 0, and Z = 16. [Page 60] The values at points B and C must be found by solving simultaneous equations. Note that point B is formed by the intersection of the lines x 1 + 2 x 2 = 10 and 6 x 1 + 6 x 2 = 36. First, convert both of these equations to functions of x 1 : and Now set the equations equal and solve for x 2 : Substituting x 2 = 4 into either of the two equations gives a value for x 1 : x 1 = 6 x 2 x 1 = 6 (4) x 1 = 2 Thus, at point B , x 1 = 2, x 2 = 4, and Z = 28. At point C , x 1 = 4. Substituting x 1 = 4 into the equation x 1 = 6 x 2 gives a value for x 2 : 4 = 6 x 2 x 2 = 2 Thus, x 1 = 4, x 2 = 2, and Z = 26.
Step  4.	Determine the Optimal Solution The optimal solution is at point B , where x 1 = 2, x 2 = 4, and Z = 28. The optimal solution and solutions at the other extreme points are summarized in the following figure: Optimal solution point