UNPACK

This operator is part of the relational algebra of set-valued relations proposed in Ozsoyoglu, Ozsoyoglu, & Mata (1985). (The other algebraic operators are Cartesian product, project, select, natural join, set union, set difference, set intersection, set formation, aggregation-by-template, and construct.)

If A is simple-valued, then Unpackk (R) maps each tuple t in R into a set of tuples such that each element in t[A] becomes the A-value of one resulting tuple.

Let R ∊ D be a relation included in the set of relations in the database, with A ∊ Atr(R), CA = Atr(R) − {A}. For each tuple t ∊ R, we define a set of tuples:

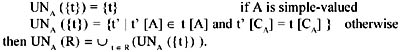
Rename

This operator is defined in different papers, such as Fortunato et al. (1986), Rafanelli & Ricci (1993), Cabibbo & Torlone (1998), Pedersen & Jensen (1999), etc.

Given a simple having scheme [A₁, A₂, …, A_n] → [M], A_i is an attribute of s₁ and A is a new attribute name, then ρ_{Ai → A} is a new MAD over the scheme [A₁, A₂, …, A_i−1, A_i+1, …, A_n, A] → [M], with a new fact name s₁'. In theory, it works on one MAD and provides as output a new MAD in which the name of one category attribute is changed (i.e., it has a new MAD schema), as well as its fact name, but in which the subject, the measure, and the structure of the old schema remain the same.

For example, suppose you wish to change the name of the category attribute Model of the MAD in Figure 16(a) and call it by the new name Modello (the Italian word of "Model"). We have:

(Model, Modello) (Number of cars produced in Japan by Modello and Year) s₁