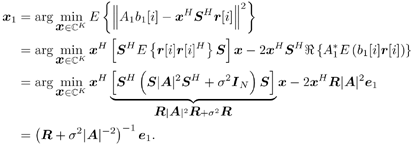2.2 Linear Receivers for Synchronous CDMA
2.2.1 Synchronous CDMA Signal ModelWe start by considering the most basic multiple-access signal model: a baseband K - user time-invariant synchronous additive white Gaussian noise (AWGN) system, employing periodic (short) spreading sequences and operating with a coherent BPSK modulation format. (An approach to adaptive detection in (long) aperiodic code DS-SS systems is developed in [61].) As noted in Chapter 1, the continuous-time waveform received by a given user in such a system can be modeled as follows : Equation 2.1 where M is the number of data symbols per user in the data frame of interest; T is the symbol interval; A k , Equation 2.2 where N is the processing gain, At the receiver, the received signal r ( t ) is filtered by a chip-matched filter and then sampled at the chip rate. The sample corresponding to the j th chip of the i th symbol is thus given by Equation 2.3 The resulting discrete-time signal corresponding to the i th symbol is then given by Equation 2.4 Equation 2.5 with where Suppose that we are interested in demodulating the data bits of a particular user, say user 1, Equation 2.6 Equation 2.7 Note that the linear equalizers and multiuser detectors discussed in Chapter 1 can all be written in this form, as will be seen below. In case the complex amplitude A 1 of the desired user is unknown, we can resort to differential detection. Define the differential bit as Equation 2.8 Then using the linear detector output [1] (2.6), the following differential detection rule can be used:
Equation 2.9 Substituting (2.4) into (2.6), the output of the linear receiver w 1 can be written as Equation 2.10 In (2.10), the first term on the right-hand side contains the useful signal of the desired user, the second term contains the signals from other undesired users ”the multiple-access interference (MAI), and the last term contains the ambient Gaussian noise. The simplest linear receiver is the conventional matched filter, where w 1 = s 1 . As noted in Chapter 1, such a matched-filter receiver is optimal only in a single-user channel (i.e., K = 1). In a multiuser channel (i.e., K > 1), this receiver may perform poorly since it makes no attempt to ameliorate the MAI, a limiting source of interference in multiple-access channels. Two popular forms of linear detectors that are capable of suppressing the MAI are the linear decorrelating detector and the linear minimum mean-square-error (MMSE) detector, which are discussed next . 2.2.2 Linear Decorrelating Detector A linear decorrelating detector for user 1, Equation 2.11 Equation 2.12 Denote by e k a K -vector with all entries zeros except for the k th entry, which is 1. Assume that the user signature sequences are linearly independent [i.e., the matrix Proposition 2.1: The linear decorrelating detector for user 1 is given by Equation 2.13 Proof: It is easily verified that Equation 2.14 Therefore, (2.11) and (2.12) hold. The output of the linear decorrelating detector is given by Equation 2.15 with Equation 2.16 where, by (2.13), Equation 2.17 and where in (2.17), [ A ] i,j denotes the ( i , j )th element of the matrix A . Note that by the Cauchy “Schwartz inequality, we have Equation 2.18 Since s 1 = 1 and 2.2.3 Linear MMSE Detector While the linear decorrelating detector is designed to eliminate the MAI completely at the expense of enhancing the ambient noise, the linear MMSE detector, Equation 2.19 Denote Proposition 2.2: The linear MMSE detector for user 1 is given by Equation 2.20 Proof: First note that any linear detector must lie in the column space of S [i.e., m 1 Equation 2.21 Hence (2.20) is obtained. The output of the linear MMSE detector is given by Equation 2.22 with Equation 2.23 where, using (2.20), we have Equation 2.24 Equation 2.25 Note that unlike the decorrelator output (2.15), the linear MMSE detector output (2.22) contains some residual MAI. However, we will in general have m 1 < d 1 , so that the effects of ambient noise are reduced by the linear MMSE detector. |
EAN: 2147483647
Pages: 91

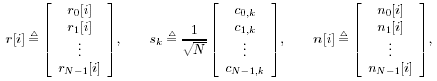
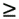 1. Hence, by (2.16), we have Var{
1. Hence, by (2.16), we have Var{ 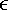 range (
range (