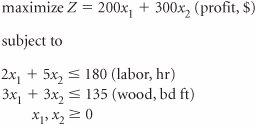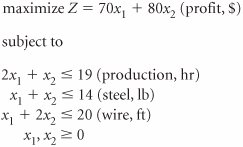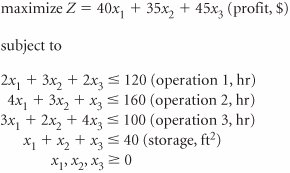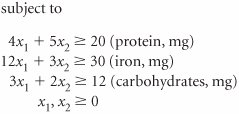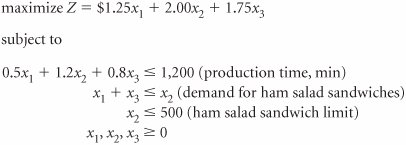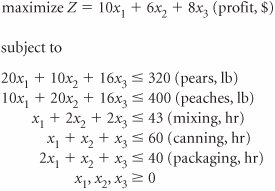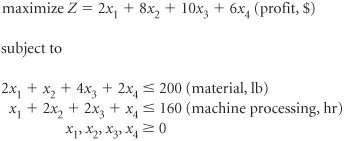Problems
| 1. | Following is a simplex tableau for a linear programming model.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | The following is a simplex tableau for a linear programming model.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. | The following is a simplex tableau for a linear programming problem.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. | The following is a simplex tableau for a linear programming problem.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. | Given is the following simplex tableau for a linear programming problem.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. | Following is a simplex tableau for a linear programming problem.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. | The Munchies Cereal Company makes a cereal from several ingredients. Two of the ingredients , oats and rice, provide vitamins A and B. The company wants to know how many ounces of oats and rice it should include in each box of cereal to meet the minimum requirements of 48 milligrams of vitamin A and 12 milligrams of vitamin B while minimizing cost. An ounce of oats contributes 8 milligrams of vitamin A and 1 milligram of vitamin B, whereas an ounce of rice contributes 6 milligrams of vitamin A and 2 milligrams of vitamin B. An ounce of oats costs $0.05, and an ounce of rice costs $0.03. Formulate a linear programming model for this problem and solve using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. | A company makes product 1 and product 2 from two resources. The linear programming model for determining the amounts of product 1 and 2 to produce ( x 1 and x 2 ) is Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. | A company produces two products that are processed on two assembly lines. Assembly line 1 has 100 available hours, and assembly line 2 has 42 available hours. Each product requires 10 hours of processing time on line 1, while on line 2 product 1 requires 7 hours and product 2 requires 3 hours. The profit for product 1 is $6 per unit, and the profit for product 2 is $4 per unit. Formulate a linear programming model for this problem and solve using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. | The Pinewood Furniture Company produces chairs and tables from two resources labor and wood. The company has 80 hours of labor and 36 pounds of wood available each day. Demand for chairs is limited to 6 per day. Each chair requires 8 hours of labor and 2 pounds of wood to produce, while a table requires 10 hours of labor and 6 pounds of wood. The profit derived from each chair is $400 and from each table, $100. The company wants to determine the number of chairs and tables to produce each day to maximize profit. Formulate a linear programming model for this problem and solve using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. | The Crumb and Custard Bakery makes both coffee cakes and Danish in large pans. The main ingredients are flour and sugar. There are 25 pounds of flour and 16 pounds of sugar available and the demand for coffee cakes is 8. Five pounds of flour and 2 pounds of sugar are required to make one pan of coffee cake, and 5 pounds of flour and 4 pounds of sugar are required to make one pan of Danish. One pan of coffee cake has a profit of $1, and one pan of Danish has a profit of $5. Determine the number of pans of cake and Danish that the bakery must produce each day so that profit will be maximized. Formulate a linear programming model for this problem and solve using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12. | The Kalo Fertilizer Company makes a fertilizer using two chemicals that provide nitrogen, phosphate, and potassium. A pound of ingredient 1 contributes 10 ounces of nitrogen and 6 ounces of phosphate, whereas a pound of ingredient 2 contributes 2 ounces of nitrogen, 6 ounces of phosphate, and 1 ounce of potassium. Ingredient 1 costs $3 per pound, and ingredient 2 costs $5 per pound . The company wants to know how many pounds of each chemical ingredient to put into a bag of fertilizer to meet minimum requirements of 20 ounces of nitrogen, 36 ounces of phosphate, and 2 ounces of potassium while minimizing cost. Formulate a linear programming model for this problem and solve using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13. | Solve the following model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14. | The Copperfield Mining Company owns two mines, both of which produce three grades of ore high, medium, and low. The company has a contract to supply a smelting company with at least 12 tons of high-grade ore, 8 tons of medium-grade ore, and 24 tons of low-grade ore. Each mine produces a certain amount of each type of ore each hour it is in operation. Mine 1 produces 6 tons of high-grade, 2 tons of medium-grade, and 4 tons of low-grade ore per hour. Mine 2 produces 2 tons of high-grade, 2 tons of medium-grade, and 12 tons of low-grade ore per hour. It costs $200 per hour to mine each ton of ore from mine 1, and it costs $160 per hour to mine a ton of ore from mine 2. The company wants to determine the number of hours it needs to operate each mine so that contractual obligations can be met at the lowest cost. Formulate a linear programming model for this problem and solve using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15. | A marketing firm has contracted to do a survey on a political issue for a Spokane television station. The firm conducts interviews during the day and at night, by telephone and in person. Each hour an interviewer works at each type of interview results in an average number of interviews. In order to have a representative survey, the firm has determined that there must be at least 400 day interviews, 100 personal interviews, and 1,200 interviews overall. The company has developed the following linear programming model to determine the number of hours of telephone interviews during the day ( x 1 ), telephone interviews at night ( x 2 ), personal interviews during the day ( x 3 ), and personal interviews at night ( x 4 ) that should be conducted to minimize cost. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16. | A jewelry store makes both necklaces and bracelets from gold and platinum . The store has developed the following linear programming model for determining the number of necklaces and bracelets ( x 1 and x 2 ) that it needs to make to maximize profit. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17. | A sporting goods company makes baseballs and softballs on a daily basis from leather and yarn. The company has developed the following linear programming model for determining the number of baseballs and softballs to produce ( x 1 and x 2 ) to maximize profits: Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18. | A clothing shop makes suits and blazers . Three main resources are used: material, rack space, and labor. The shop has developed this linear programming model for determining the number of suits and blazers to make ( x 1 and x 2 ) to maximize profits: Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19. | Solve the following linear programming model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20. | The following is a simplex tableau for a linear programming model.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21. | A wood products firm in Oregon plants three types of trees white pines, spruce, and ponderosa pines to produce pulp for paper products and wood for lumber. The company wants to plant enough acres of each type of tree to produce at least 27 tons of pulp and 30 tons of lumber. The company has developed the following linear programming model to determine the number of acres of white pines ( x 1 ), spruce ( x 2 ), and ponderosa pines ( x 3 ) to plant to minimize cost. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22. | A baby products firm produces a strained baby food containing liver and milk, each of which contribute protein and iron to the baby food. Each jar of baby food must have 36 milligrams of protein and 50 milligrams of iron. The company has developed the following linear programming model to determine the number of ounces of liver ( x 1 ) and milk ( x 2 ) to include in each jar of baby food to meet the requirements for protein and iron at the minimum cost. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23. | Solve the linear programming model in problem 22 graphically, and identify the points on the graph that correspond to each simplex tableau. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24. | The Cookie Monster Store at South Acres Mall makes three types of cookieschocolate chip, pecan chip, and pecan sandies. Three primary ingredients are chocolate chips, pecans, and sugar. The store has 120 pounds of chocolate chips, 40 pounds of pecans, and 300 pounds of sugar. The following linear programming model has been developed for determining the number of batches of pecan chip cookies ( x 1 ), chocolate chip cookies ( x 2 ), and pecan sandies ( x 3 ) to make to maximize profit. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25. | The Eastern Iron and Steel Company makes nails , bolts, and washers from leftover steel and coats them with zinc. The company has 24 tons of steel and 30 tons of zinc. The following linear programming model has been developed for determining the number of batches of nails ( x 1 ), bolts ( x 2 ), and washers ( x 3 ) to produce to maximize profit. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26. | Solve the following linear programming model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27. | Solve the following linear programming model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28. | Solve the linear programming model in problem 27 graphically, and identify the points on the graph that correspond to each simplex tableau. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29. | Transform the following linear programming model into proper form for solution by the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30. | Transform the following linear programming model into proper form for solution by the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31. | A manufacturing firm produces two products using labor and material. The company has a contract to produce 5 of product 1 and 12 of product 2. The company has developed the following linear programming model to determine the number of units of product 1 ( x 1 ) and product 2 ( x 2 ) to produce to maximize profit. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32. | A custom tailor makes pants and jackets from imported Irish wool cloth. To get any cloth at all, the tailor must purchase at least 25 square feet each week. Each pair of pants and each jacket requires 5 square feet of material. The tailor has 16 hours available each week to make pants and jackets. The demand for pants is never more than 5 pairs per week. The tailor has developed the following linear programming model to determine the number of pants ( x 1 ) and jackets ( x 2 ) to make each week to maximize profit. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33. | A sawmill in Tennessee produces cherry and oak boards for a large furniture manufacturer. Each month the sawmill must deliver at least 5 tons of wood to the manufacturer. It takes the sawmill 3 days to produce a ton of cherry and 2 days to produce a ton of oak, and the sawmill can allocate 18 days out of a month for this contract. The sawmill can get enough cherry to make 4 tons of wood and enough oak to make 7 tons of wood. The sawmill owner has developed the following linear programming model to determine the number of tons of cherry ( x 1 ) and oak ( x 2 ) to produce to minimize cost. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34. | Solve the following linear programming model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35. | Solve the following linear programming problem using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36. | Solve the following linear programming problem using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37. | A farmer has a 40-acre farm in Georgia. The farmer is trying to determine how many acres of corn, peanuts, and cotton to plant. Each crop requires labor, fertilizer, and insecticide. The farmer has developed the following linear programming model to determine the number of acres of corn ( x 1 ), peanuts ( x 2 ), and cotton (x 3 ) to plant to maximize profit. Solve this model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38. | Solve the following linear programming model (a) graphically and (b) using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39. | Solve the following linear programming model (a) graphically and (b) using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40. | Solve the following linear programming model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41. | Solve the following linear programming model using the simplex method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42. | The Old English Metal Crafters Company makes brass trays and buckets. The number of trays ( x 1 ) and buckets ( x 2 ) that can be produced daily is constrained by the availability of brass and labor, as reflected in the following linear programming model. The final optimal simplex tableau for this model is as follows .
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43. | The Southwest Foods Company produces two brands of chiliRazorback and Longhornfrom several ingredients, including chili beans and ground beef. The number of 100-gallon batches of Razorback chili ( x 1 ) and Longhorn chili ( x 2 ) that can be produced daily is constrained by the availability of chili beans and ground beef, as shown in the following linear programming model. The final optimal simplex tableau for this model is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44. | The Agrimaster Company produces two kinds of fertilizer spreadersregular and cyclone. Each spreader must undergo two production processes. Letting x 1 The final optimal simplex tableau for this problem is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45. | The Stratford House Furniture Company makes two kinds of tablesend tables ( x 1 ) and coffee tables ( x 2 ). The manufacturer is restricted by material and labor constraints, as shown in the following linear programming formulation. The final optimal simplex tableau for this problem is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46. | A manufacturing firm produces electric motors for washing machines and vacuum cleaners. The firm has resource constraints for production time, steel, and wire. The linear programming model for determining the number of washing machine motors ( x 1 ) and vacuum cleaner motors ( x 2 ) to produce has been formulated as follows. The final optimal simplex tableau for this model is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47. | A manufacturer produces products 1 and 2, for which profits are $9 and $12, respectively. Each product must undergo two production processes that have labor constraints. There are also material constraints and storage limitations. The linear programming model for determining the number of product 1 to produce ( x 1 ) and the number of product 2 to product ( x 2 ) is given as follows. The final optimal simplex tableau for this model is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48. | A manufacturer produces products 1, 2, and 3 daily. The three products are processed through three production operations that have time constraints, and the finished products are then stored. The following linear programming model has been formulated to determine the number of product 1( x 1 ), product 2( x 2 ), and product 3( x 3 ) to produce. The final optimal simplex tableau for this model is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49. | A school dietitian is attempting to plan a lunch menu that will minimize cost and meet certain minimum dietary requirements. The two staples in the meal are meat and potatoes, which provide protein, iron, and carbohydrates. The following linear programming model has been formulated to determine how many ounces of meat ( x 1 ) and ounces of potatoes ( x 2 ) to put in a lunch. The final optimal simplex tableau for this model is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50. | The Overnight Food Processing Company prepares sandwiches (among other processed food items) for vending machines, markets, and business canteens around the city. The sandwiches are made at night and delivered early the following morning. Any sandwiches not purchased during the previous day are thrown away. Three kinds of sandwiches are made each night, a basic cheese sandwich ( x 1 ), a ham salad sandwich ( x 2 ), and a pimento cheese sandwich ( x 3 ). The profits are $1.25, $2.00, and $1.75, respectively. It takes 0.5 minutes to make a cheese sandwich, 1.2 minutes to make a ham salad sandwich, and 0.8 minutes to make a pimento cheese sandwich. The company, has 20 hours of labor available to produce the sandwiches each night. The demand for ham salad sandwiches is at least as great as the demand for the two types of cheese sandwiches combined. However, the company has only enough ham salad to produce 500 sandwiches per night. The company has formulated the following linear programming model in order to determine how many of each type of sandwich to make to maximize profit. The optimal simplex tableau follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51. | Given the linear programming model, and its optimal simplex tableau,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52. | The Sunshine Food Processing Company produces three canned fruit productsmixed fruit ( x 1 ), fruit cocktail ( x 2 ), and fruit delight ( x 3 ). The main ingredients in each product are pears and peaches. Each product is produced in lots and must undergo three processesmixing, canning, and packaging. The resource requirements for each product and each process are shown in the following linear programming formulation. The optimal simplex tableau is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53. | The Evergreen Products Firm produces three types of pressed paneling from pine and spruce. The three types of paneling are Western ( x 1 ), Old English ( x 2 ), and Colonial ( x 3 ). Each sheet must be cut and pressed. The resource requirements are given in the following linear programming formulation. The optimal simplex tableau is as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54. | A manufacturing firm produces four products. Each product requires material and machine processing. The linear programming model formulated to determine the number of product 1 ( x 1 ), product 2 ( x 2 ), product 3 ( x 3 ), and product 4 ( x 4 ) to produce is as follows. The optimal simplex tableau is as follows.
What is the marginal value of an additional pound of material? Over what range is this value valid? |
EAN: 2147483647
Pages: 358
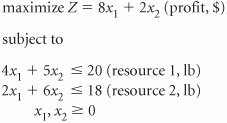


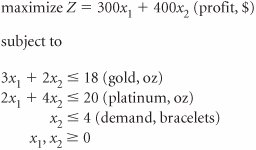

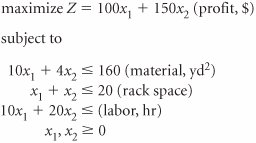
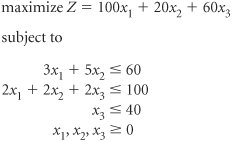
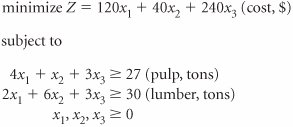
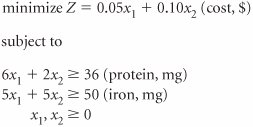
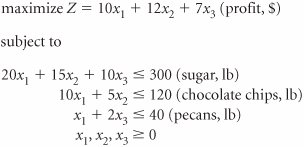

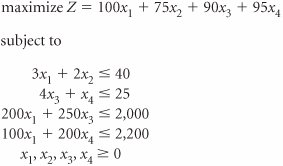
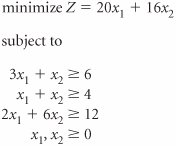
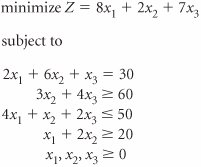
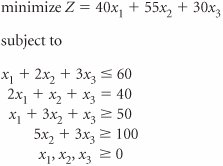

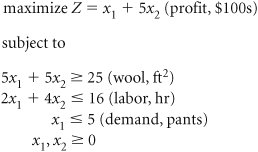
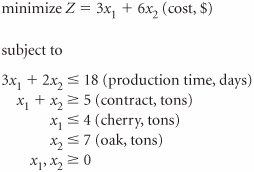
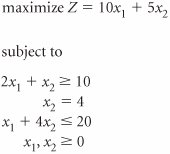
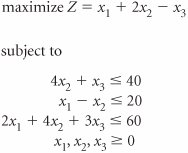
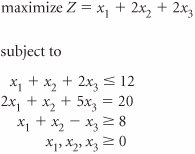

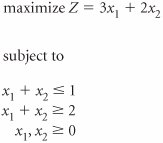
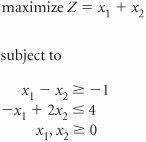
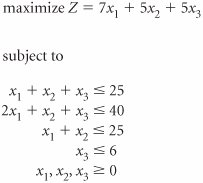
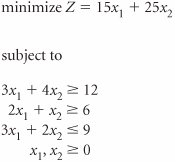
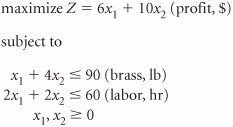
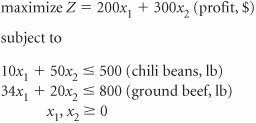
 the number of regular spreaders produced and
the number of regular spreaders produced and