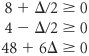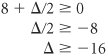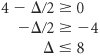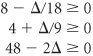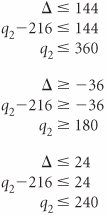Sensitivity Analysis
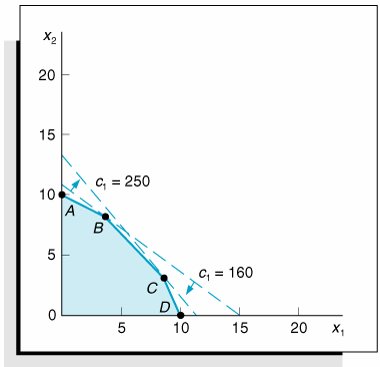
| In this section we will show how sensitivity ranges are mathematically determined using the simplex method. While this is not as efficient or quick as using the computer, close examination of the simplex method for performing sensitivity analysis can provide a more thorough understanding of the topic. Changes in Objective Function CoefficientsTo demonstrate sensitivity analysis for the coefficients in the objective function, we will use the Hickory Furniture Company example developed in the previous section. The model for this example was formulated as where x 1 = number of tables produced x 2 = number of chairs produced The coefficients in the objective function will be represented symbolically as c j (the same notation used in the simplex tableau). Thus, c 1 = 160 and c 2 = 200. Now, let us consider a change in one of the c j values by an amount D . For example, let us change c 1 = 160 by D = 90. In other words, we are changing c 1 from $160 to $250. The effect of this change on the solution of this model is shown graphically in Figure A-10. Figure A-10. A change in c 1 Originally, the solution to this problem was located at point B in Figure A-10, where x 1 = 4 and x 2 = 8. However, increasing c 1 from $160 to $250 shifts the slope of the objective function so that point C ( x 1 = 8, x 2 = 4) becomes the optimal solution. This demonstrates that a change in one of the coefficients of the objective function can change the optimal solution. Therefore, sensitivity analysis is performed to determine the range over which c j can be changed without altering the optimal solution. The sensitivity range for a c j value is the range of values over which the current optimal solution will remain optimal. The range of c j that will maintain the optimal solution can be determined directly from the optimal simplex tableau. The optimal simplex tableau for our furniture company example is shown in Table A-33. Table A-33. The Optimal Simplex Tableau
D is added to c j in the optimal simplex tableau. First, consider a D change for c 1 . This will change the c 1 value from c 1 = 160 to c 1 = 160 + D , as shown in Table A-34. Notice that when c 1 is changed to 160 + D , the new value is included not only in the top c j row but also in the left-hand c j column. This is because x 1 is a basic solution variable. Since 160 + D is in the left-hand column, it becomes a multiple of the column values when the new z j row values and the subsequent c j z j row values, also shown in Table A-34, are computed. Table A-34. The Optimal Simplex Tableau with c 1 = 160 + D
For the solution to remain optimal all values in the c j z j row must be The solution shown in Table A-34 will remain optimal as long as the c j z j row values remain negative. (If c j z j becomes positive, the product mix will change, and if it becomes zero, there will be an alternative solution.) Thus, for the solution to remain optimal, 20 + D /2 and 20/3 D /9 Both of these inequalities must be solved for D . and Thus, D and Therefore, the range of values for c 1 over which the solution basis will remain optimal (although the value of the objective function may change) is 100 Next, consider a D change in c 2 so that c 2 = 200 + D . The effect of this change in the final simplex tableau is shown in Table A-35. Table A-35. The Optimal Simplex Tableau with c 2 = 200 + D(This item is displayed on page A-37 in the print version)
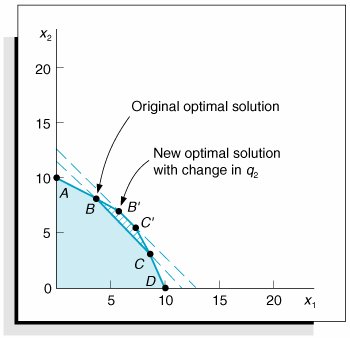
As before, the solution shown in Table A-35 will remain optimal as long as the c j z j row values remain negative or zero. Thus, for the solution to remain optimal, we must have 20 D /2 and 20/3 + D /18 Solving these inequalities for D gives and Thus, D and Therefore, the range of values for c 2 over which the solution will remain optimal is 160 The ranges for both objective function coefficients are as follows . 100 160 However, these ranges reflect a possible change in either c 1 or c 2 , not simultaneous changes in both c 1 and c 2 . Both of the objective function coefficients in this example were for basic solution variables. Determining the c j sensitivity range for a decision variable that is not basic is much simpler. Because it is not in the basic variable column, the D change does not become a multiple of the z j row. Thus, the D change will show up in only one column in the c j z j row. Changes in Constraint Quantity ValuesTo demonstrate the effect of a change in the quantity values of the model constraints, we will again use the Hickory Furniture Company example. The quantity values 40, 216, and 240 will be represented symbolically as q i . Thus, q 1 = 40, q 2 = 216, and q 3 = 240. Now consider a D change in q 2 . For example, let us change q 2 = 216 by D = 18. In other words, q 2 is changed from 216 board feet to 234 board feet. The effect of this change is shown graphically in Figure A-11. Figure A-11. A D change in q 2 In Figure A-11 a change in q 2 is shown to have the effect of changing the feasible solution area from 0 ABCD to 0 AB'C'D . Originally, the optimal solution point was B ; however, the change in q 2 causes 'B to be the new optimal solution point. At point B the optimal solution is
At point B' the new optimal solution is
Thus, a change in a q i value can change the values of the optimal solution. At some point an increase or decrease in q i will change the variables in the optimal solution mix, including the slack variables. For example, if q 2 increases to 240 board feet, then the optimal solution point will be at
Notice that s 3 has left the solution; thus, the optimal solution mix has changed. At this point, where q 2 = 240, which is the upper limit of the sensitivity range for q 2 , the shadow price will also change. Therefore, the purpose of sensitivity analysis is to determine the range for q i over which the optimal variable mix will remain the same and the shadow price will remain the same. The sensitivity range for a q i , value is the range of values over which the right-hand-side values can vary without changing the solution variable mix, including slack variables and the shadow prices. As in the case of the c j values, the range for q i can be determined directly from the optimal simplex tableau. As an example, consider a D increase in the number of labor hours. The model constraints become Notice in the initial simplex tableau for our example (Table A-36) that the changes in the quantity column are the same as the coefficients in the s 1 column. Table A-36. The Initial Simplex Tableau
A D in a q i value is duplicated in the s i column in the final tableau. This duplication will carry through each subsequent tableau, so the s 1 column values will duplicate the D changes in the quantity column in the final tableau (Table A-37). Table A-37. The Final Simplex Tableau(This item is displayed on page A-40 in the print version)
In effect, the D changes form a separate column identical to the s 1 column. Therefore, to determine the D change, we need only observe the slack ( s i ) column corresponding to the model constraint quantity ( q i ) being changed. Recall that a requirement of the simplex method is that the quantity values not be negative. If any q i value becomes negative, the current solution will no longer be feasible and a new variable will enter the solution. Thus, the inequalities are solved for D : and and Since q 1 = 40 + D then D = q 1 40 These values are substituted into the inequalities D Summarizing these inequalities, we have 24 The value of 24 can be eliminated, since q 1 must be greater than 32; thus, 32 As long as q 1 remains in this range, the present basic solution variables will remain the same and feasible. However, the quantity values of those basic variables may change. In other words, although the variables in the basis remain the same, their values can change. To determine the range for q 2 (where q 2 = 216 + D ), the s 2 column values are used to develop the D inequalities. The inequalities are solved as follows. Since q 2 = 216 + D we have D = q 2 216 Substituting this value into the inequalities D That is, 180 The value 360 can be eliminated, because q 2 cannot exceed 240. Thus, the range over which the basic solution variables will remain the same is 180 The range for q 3 is 192 The upper limit of Sensitivity analysis of constraint quantity values can be used in conjunction with the dual solution to make decisions regarding model resources. Recall from our analysis of the dual solution of the Hickory Furniture Company example that y 1 = $20, marginal value of labor y 2 = $6.67, marginal value of wood y 3 = $0, marginal value of storage space The shadow prices are only valid with the sensitivity range for the right-hand-side values. Because the resource with the greatest marginal value is labor, the manager might desire to secure some additional hours of labor. How many hours should the manager get? Given that the range for q 1 is 32
Since D = 8,
Total profit will be increased by $20 for each extra hour of labor.
In this example for the Hickory Furniture Company, we considered only | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EAN: 2147483647
Pages: 358
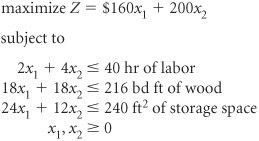
 0.
0. 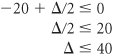
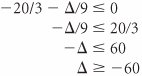
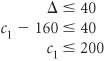
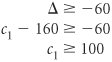
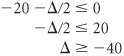

 40 and 120. Since
40 and 120. Since