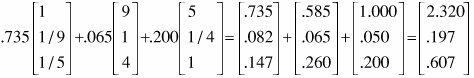Approximations to AHP with Manual Calculations

The following two solutions illustrate approximations to some of the AHP calculations that are performed with Expert Choice. Although these approximate calculations can be somewhat tedious and may not produce the same results, particularly when there are some inconsistencies in judgments, they give you a more detailed look at some of AHP's intricacies.

We will illustrate two approximate methods for arriving at an AHP solution to Case Study 8.1. The approximations can be good in some cases but not so good in others. In general, the smaller the clusters in an AHP model and the more consistent the judgments, the more accurate the approximate calculations will be. Following this approximate solution, we will present another variationthe one by Michael Brassard.

Approximate Solution Method 1

Step 1: Brainstorm and Construct a Hierarchical Model of the Problem

Step 1 in the solution derivation is same as the one used earlier, in the section "Case Study 8.1 Solution Using Expert Choice."

Step 2: Construct a Pairwise Comparison Matrix for the Objectives

To establish the priority ranking among the three alternatives, AHP uses pairwise relative comparisons. A decision-maker stipulates his or her judgments regarding the relative importance of the objectives in attaining the overall goal.

The decision-maker's judgments are entered into the elements above the diagonal in Table 8.3 using the numeric representation of Saaty's verbal scale. The diagonal elements of Table 8.3 are all 1 because an element's importance when compared to itself is 1. The elements below the diagonal are the reciprocals of the elements above the diagonals, as per Axiom 2 of AHP (if A is n x B, B is 1/ n x A). A fractional judgment, such as 1/3 when comparing the row element Implementation Cost to the column element Technical Risk, means that the column element is more important than the row elementin this case, moderately more important.

Table 8.3. Pairwise Comparison Matrix for the Objectives

	Implementation Cost	Technical Risk	Business Risk	Competitive Advantage	Time to Implement	Approximate Weight	Eigen-vector Weight
Implementation Cost	1	1/3	1/9	1/9	1/5	1.756 (.031)	.033
Technical Risk	3	1	1/5	1/6	1	5.367 (.093)	.083
Business Risk	9	5	1	1	5	21.000 (.364)	.386
Competitive Advantage	9	6	1	1	5	22.000 (.383)	.402
Time to Implement	5	1	1/5	1/5	1	7.400 (.129)	.097
Total						57.523

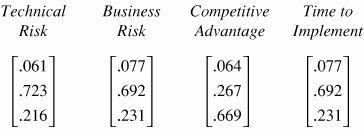
Because it is not easy to calculate the principal right eigenvector manually, an approximate technique is used in which the priorities are approximated by the normalized sum of the judgments in each of the rows (or columns). For example, in Table 8.3, the pairwise judgments are summed for each row. The sums are then normalized, as shown in the last column of Table 8.3. The "weights" represent an approximation to the relative importance or priorities of the objectives. For example, the priority of Implementation Cost using this approximate technique is .031, and the exact solution, computed by Expert Choice, is .033. Similarly, the approximate priority for Competitive Advantage is .383, and the exact solution is .402. The more consistent the judgments, the closer the approximate solution is to the exact solution.

Step 3: Construct a Pairwise Comparison Matrix for the Alternatives

This step involves pairwise comparisons of the alternatives with respect to each objective in separate matrices, one for each objective. The procedure is similar to the one used for constructing pairwise matrix for objectives. The question to ask here is, which alternative is relatively more important than the other in terms of its contribution toward achieving the particular objective being considered? The five matrices are constructed as shown in Tables 8.4 through 8.8.

Table 8.4. Pairwise Comparison Matrix for the Alternatives Vis-à-Vis Implementation Cost

	Alternative A	Alternative B	Alternative C
Alternative A	1	9	5
Alternative B	1/9	1	1/4
Alternative C	1/5	4	1

Table 8.5. Pairwise Comparison Matrix for the Alternatives Vis-à-Vis Technical Risk

	Alternative A	Alternative B	Alternative C
Alternative A	1	1/9	1/5
Alternative B	9	1	5
Alternative C	5	1/5	1

Table 8.6. Pairwise Comparison Matrix for the Alternatives Vis-à-Vis Business Risk

	Alternative A	Alternative B	Alternative C
Alternative A	1	1/9	1/3
Alternative B	9	1	3
Alternative C	3	1/3	1

Table 8.7. Pairwise Comparison Matrix for the Alternatives Vis-à-Vis Competitive Advantage

	Alternative A	Alternative B	Alternative C
Alternative A	1	1/5	1/9
Alternative B	5	1	1/3
Alternative C	9	3	1

Table 8.8. Pairwise Comparison Matrix for the Alternatives Vis-à-Vis Time to Implement

	Alternative A	Alternative B	Alternative C
Alternative A	1	1/9	1/3
Alternative B	9	1	3
Alternative C	3	1/3	1

Step 4: Approximate the Priorities from the Judgments

After the various matrices have been constructed, we need to determine the alternatives' priorities with respect to each of the covering objectives. As mentioned earlier, this involves a mathematical computation of eigenvalues and eigenvectors that is beyond the scope of this book. We will use the following procedure, which is a good approximation of the synthesized priorities:^[14]

1.	Sum the values of the elements in the pairwise comparison matrix.
2.	Divide each element in the pairwise comparison matrix by its column total. The resulting matrix is called the normalized pairwise comparison matrix.
3.	Compute the average of the elements in each row of the normalized matrix. These averages provide an estimate of the relative priorities of the elements being compared.

This three-step procedure is carried out for the pairwise comparison matrix for the alternatives vis-à-vis Implementation Cost (see Table 8.4). It results in the normalized pairwise comparison matrix shown in Table 8.9. The three-step construction of the normalized matrix is shown in Tables 8.9 through 8.11.

Table 8.9. Sum the Values in Each Column

	Alternative A	Alternative B	Alternative C
Alternative A	1	9	5
Alternative B	1/9	1	1/4
Alternative C	1/5	4	1
Totals	59/45	14	25/4

Table 8.10. Divide Each Matrix Element by Its Column Total

	Alternative A	Alternative B	Alternative C
Alternative A	45/59	9/14	20/25
Alternative B	5/59	1/14	1/25
Alternative C	9/59	4/14	4/25

Table 8.11. Average the Elements in Each Row

	Alternative A	Alternative B	Alternative C	Row Average
Alternative A	.763	.643	.800	.735
Alternative B	.085	.071	.040	.065
Alternative C	.152	.286	.160	.200
				Total = 1.000

The preceding calculations provide the priorities for the three alternatives vis-à-vis the Implementation Cost objective.

The priority vector with respect to Implementation Cost is

compared to the exact solution obtained with Expert Choice:

Similarly, the priority vectors for the other objectives are calculated and are as follows:

The exact solution obtained with Expert Choice is

Because the inconsistencies of the judgments are rather small for these matrices, the approximate priorities are close to those obtained with Expert Choice. In fact, they are exactly the same for the two matrices that are perfectly consistent. You will next see how to manually approximate the calculations of the judgment consistencies.

Step 5: Estimate the Consistency Ratio

AHP does not require perfectly consistent judgments, but it provides an index for measuring consistency for each matrix and for the entire hierarchy. Thus, it is possible to find where the inconsistent judgments are. You can change them if you want to, although this is not required. The goal is not to be perfectly consistent, but to be as accurate as possible. A certain amount of inconsistency is required to learn new things.^[15] A inconsistency index of .10 or less is usually considered reasonable.

An approximate computation of consistency index and consistency ratio (or what Expert Choice calls the inconsistency ratio, because the higher the value, the more inconsistent the judgments) is as follows:^[16]

1. Multiply each value in the first column of the pairwise comparison matrix by the relative priority of the first item considered. Multiply each value in the second column of the matrix by the relative priority of the second item considered. Multiply each value in the third column of the matrix by the relative priority of the third item considered. Sum the values across the rows to obtain a vector of values labeled "weighted sum." This computation for the MIS director's IT dilemma case is as follows:

   

   
   

2. Divide the elements of the vector of weighted sums you just obtained by the corresponding priority value. You obtain the following:

   2.320/.735 = 3.156

   .197/.065 = 3.030

   .607/.200 = 3.035

3. Compute the average of the three:

   λ_max = (3.156 + 3.030 + 3.035)/3 = 3.074

4. Compute the consistency index (CI):

   CI = (λ_max n)/(n 1)

   where n = the number of items being compared.

   For the MIS Director's IT Dilemma case, with n = 3, you obtain the following:

   CI = (3.074 3)/2 = .037

5. Compute the consistency ratio (CR):

   CR = CI/RI

   where the random index (RI) is the average consistency index of many simulated pairwise comparison matrices of random judgments. The RI, which depends on the number of elements being compared, takes on the following values:

   n	3	4	5	6	7	8
   RI	.58	.90	1.12	1.24	1.32	1.41

   
   

   For the MIS Director's IT Dilemma case, when n = 3 and RI = 0.58, we get

   CR = .037/0.58 = .064

   This value for CR, less than .1, is acceptable.

Step 6: Develop the Overall Priority Ranking

Following the preceding computations, the priority vectors for all the objectives are tabulated as shown in Table 8.12.

Table 8.12. The Priority Vectors for the MIS Director's IT Dilemma

Objective Alternative	Implementation Cost	Technical Risk	Business Risk	Competitive Advantage	Time to Implement
Alternative A	.735	.061	.077	.064	.077
Alternative B	.065	.723	.692	.267	.692
Alternative C	.200	.216	.231	.669	.231

Table 8.12 reveals the following priorities:

• Alternative A is most preferable for Implementation Cost.

• Alternative B is most preferable for Technical Risk, Business Risk, and Time to Implement.

• Alternative C is most preferable for Competitive Advantage.

No alternative is most preferred for all the objectives. Therefore, to make a choice, we need to look at the relative importance of all the alternatives computed in Table 8.3. The objective priorities from that table appear in Table 8.13.

Table 8.13. Relative Ranking of Various Objectives

Objective	Weight
Implementation Cost	.031
Technical Risk	.093
Business Risk	.364
Competitive Advantage	.383
Time to Implement	.129
	Total = 1.000

The overall priority of each alternative can be calculated by summing the products of the objective priority and multiplying by the priority of its decision alternative, as shown in Table 8.13. We can compute overall ranking priority as follows:

Alternative A = .031(.735) + .093(.061) + .364(.077) + .383(.064) + .129(.077) = .091

Alternative B = .031(.065) + .093(.723) + .364(.692) + .383(.267) + .129(.692) = .513

Alternative C = .031(.200) + .093(.216) + .364(.231) + .383(.669) + .129(.231) = .396

This gives us the overall rankings shown in Table 8.14.

Table 8.14. Overall Priorities and Rankings of the Three Alternatives

Alternative	Priorities from Approximate Calculations (Method 1)	Priorities from Exact Calculations (Distributive Mode)	Priorities from Exact Calculations (Ideal Mode)
Alternative A	.091	.091	.090
Alternative B	.513	.504	.501
Alternative C	.396	.405	.409

The preceding provides the following rankings:

Rank 1: Alternative B

Rank 2: Alternative C

Rank 3: Alternative A

You can see that, for this simple example, the priorities from the approximate calculations are very close to the Ideal Mode exact calculations produced by Expert Choice. (The Distributive and Ideal synthesis modes are explained in the Expert Choice solution arrived at earlier in the chapter.)

Approximate Solution Method 2: Brassard's Full Analytical Criteria Method for Prioritization

You may recall that this method was introduced in Chapter 7, along with other prioritization matricesnamely, the Consensus Criteria Method and the Combination I.D./Matrix Method. Of the three prioritization matrices developed by Brassard, the Full Analytical Criteria Method is the most rigorous and time-consuming. Although it is based on Saaty's AHP methodology, it is not nearly as accurate and can lead to different results. Nevertheless, the following sections describe the steps required to construct a Brassard Full Analytical Criteria Method.^[17]

Step 1: Agree on the Ultimate Goal to Be Achieved

We will use the MIS Director's IT Dilemma case for our analysis. This step has to do with clearly stating the ultimate goal of the prioritization process. In this case it is the "overall goal" of Case Study 8.1: "Select the best upgrade path."

Step 2: Create a List of Criteria to Be Applied to the Options Generated

The criteria or objectives are Implementation Cost, Technical Risk, Business Risk, Competitive Advantage, and Time to Implement.

Step 3: Judge the Relative Importance of Each Criterion as Compared to Every Other Criterion

Here each criterion is rated against every other criterion in a paired comparison using the following scale:

1/10 = Much less important/preferred

1/5 = Less important/preferred

1 = Equally important/preferred

5 = More important/preferred

10 = Much more important/preferred

Table 8.15 shows the pairwise comparison for the preceding criteria. It is an L-shaped matrix. A criterion when compared to itself results in a numerical score of 1. If it is more important than the criterion it is compared to, it gets a numerical score of 5. When it's less important than the criterion it is compared to, it gets a numerical score of 1/5. If it is much more important than the criterion it is compared to, it gets a numerical score of 10. If it's much less important than the criterion it is compared to, it gets a numerical score of 1/10. The individual comparative scores for each criterion are added and their proportionate weights are calculated, as shown in the last column of Table 8.15. The weights represent the relative importance or priorities of various criteria. The overall pairwise comparison is tabulated in Table 8.15.

Table 8.15. Weighing Importance of Criteria: Criterion Versus Criterion Matrix

	Implementation Cost	Technical Risk	Business Risk	Competitive Advantage	Time to Implement	Rows Total (Weights; Total % of Grand Total)
Implementation Cost		1/5	1/10	1/10	1/5	.600 (.010)
Technical Risk	5		1/5	1/5	1	6.400 (.116)
Business Risk	10	5		1	5	21.000 (.379)
Competitive Advantage	10	5	1		5	21.000 (.379)
Time to Implement	5	1	1/5	1/5		6.400 (.116)
Column Total	30	11.2	1.5	1.5	11.2	55.400 (1.000)

The row weights represent the criteria's relative importance. Of the five criteria, Business Risk and Competitive Advantage are significantly more important than Implementation Cost, Technical Risk, and Time to Implement: scores of .379 and .379 compared to .010, .116, and .116, respectively. Given such dramatic differences, the less-important criteria can be dropped from any further analysis.^[18] Therefore, we'll use just Business Risk and Competitive Advantage as the criteria against which the three alternatives (A, B, and C) will be compared to achieve the overall goal of selecting the best upgrade path.

Step 4: Compare All the Alternative Solutions to the Individual Criteria

This step involves pairwise comparison of the alternative solutions with respect to each criterion in separate matrices, one for each criterion. The procedure is similar to the one used to construct a pairwise matrix for objectives (Table 8.15). The question to ask here is, which alternative solution has a relatively greater impact than the other in terms of its contribution toward achieving the particular criterion being considered? The rows and columns are summed to get the totals, and the relative weights of each alternative solution are calculated as a percentage (fraction) of the total. The two matrices are constructed as shown in Tables 8.16 and 8.17.

Table 8.16. Solution Alternatives Versus Each Criterion Comparison Matrix: Business Risk

	Alternative A	Alternative B	Alternative C	Rows Total (Weights; % of Grand Total)
Alternative A		1/5	1	1.2 (.097)
Alternative B	5		5	10 (.806)
Alternative C	1	1/5		1.2 (.097)
Column Total	6	.4	6	12.4 (1.000)

1/10 = Much less impact

1/5 = Less impact

1 = Equal impact

5 = More impact

10 = Much more impact

Table 8.17. Solution Alternatives Versus Each Criterion Comparison Matrix: Competitive Advantage

	Alternative A	Alternative B	Alternative C	Rows Total (Weights; % of Grand Total)
Alternative A		1/10	1/5	.3 (.014)
Alternative B	10		5	15 (.732)
Alternative C	5	1/5		5.2 (.254)
Column Total	15	.3	5.2	20.5 (1.000)

1/10 = Much less impact

1/5 = Less impact

1 = Equal impact

5 = More impact

10 = Much more impact

Step 5: Compare All the Alternative Solutions Based on All Criteria Combined

This is the summary matrix and is prepared by using an L-shaped matrix (see Table 8.18). All the alternative solutions are listed on the vertical side of the matrix. All the criteria considered previously (see Tables 8.16 and 8.17) are listed on the horizontal side. All the percentage scores for the two criteria are recorded as shown. All these scores are multiplied by the weighted score of each criterion in Table 8.15.

Table 8.18. Summary Matrix Table: Alternative Solutions Versus All Criteria

Alternative	Business Risk (.379)	Competitive Advantage (.379)	Rows Total (weights; % of Grand Total)
Alternative A	.097 x .379 = .037	.014 x .379 = .005	.042 (.055)
Alternative B	.806 x .379 = .305	.732 x .379 = .277	.582 (.769)
Alternative C	.097 x .379 = .037	.254 x .379 = .096	.133 (.176)
Column Total	.379	.378	.757 (1.000)

The totals of rows and columns are calculated, as are the weights. This provides the following ranking:

Rank 1: Alternative B

Rank 2: Alternative C

Rank 3: Alternative A

The most preferable alternative overall is alternative B. For this simple example, the ranking results from Brassard's Full Analytical Criteria Method are the same as from the AHP deployments presented earlier in the chapter. As you can see from Table 8.19, alternative B has a much higher relative priority ranking using Brassard's Full Analytical Criteria Method than from Approximate Solution Method 1 and from Expert Choice, both of which are pretty close. As a manual calculation, Method 1 provides a solution that is much closer to the one obtained from Expert Choice than the one obtained from Brassard's Method. For accuracy of results, additional analytical features, and sheer convenience of use, we emphasize Expert Choice.

Table 8.19. Comparison of Priorities from AHP Exact, AHP Approximate, and Brassard's Method

Alternative	Exact Priorities from Expert Choice Software (Ideal Mode)	Priority Ranking from Approximate Calculations (Method 1)	Priority Ranking from Approximate Calculations (Brassard's Method)
Alternative A	.090	.091	.055
Alternative B	.501	.513	.769
Alternative C	.409	.396	.176