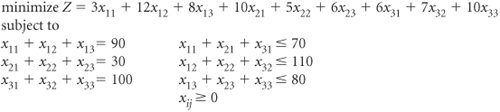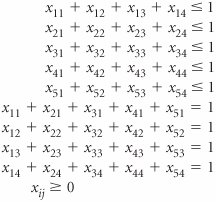Problems
| 1. | Green Valley Mills produces carpet at plants in St. Louis and Richmond. The carpet is then shipped to two outlets located in Chicago and Atlanta. The cost per ton of shipping carpet from each of the two plants to the two warehouses is as follows .
The plant at St. Louis can supply 250 tons of carpet per week; the plant at Richmond can supply 400 tons per week. The Chicago outlet has a demand of 300 tons per week, and the outlet at Atlanta demands 350 tons per week. The company wants to know the number of tons of carpet to ship from each plant to each outlet in order to minimize the total shipping cost. Solve this transportation problem. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | A transportation problem involves the following costs, supply, and demand.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
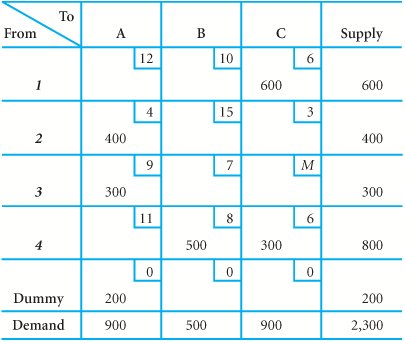
| 3. | Consider the following transportation tableau and solution.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. | Solve the following transportation problem.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. | Given a transportation problem with the following costs, supply, and demand, find the initial solution using the minimum cell cost method and Vogel's approximation model. Is the VAM solution optimal?
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. | Consider the following transportation problem.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. | Solve the following linear programming problem. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. | Consider the following transportation problem.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. | Steel mills in three cities produce the following amounts of steel .
These mills supply steel to four cities where manufacturing plants have the following demand.
Shipping costs per ton of steel are as follows.
Because of a truckers' strike, shipments are at present prohibited from Birmingham to Chicago.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. | In problem 9, what would be the effect on the optimal solution of a reduction in production capacity at the Gary mill from 320 tons to 290 tons per week? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. | Coal is mined and processed at the following four mines in Kentucky, West Virginia, and Virginia.
These mines supply the following amount of coal to utility power plants in three cities.
The railroad shipping costs ($1,000s) per ton of coal are shown in the following table. Because of railroad construction, shipments are now prohibited from Cabin Creek to Richmond.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12. | Oranges are grown, picked, and then stored in warehouses in Tampa, Miami, and Fresno. These warehouses supply oranges to markets in New York, Philadelphia, Chicago, and Boston. The following table shows the shipping costs per truckload ($100s), supply, and demand. Because of an agreement between distributors , shipments are prohibited from Miami to Chicago.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13. | A manufacturing firm produces diesel engines in four citiesPhoenix, Seattle, St. Louis, and Detroit. The company is able to produce the following numbers of engines per month.
Three trucking firms purchase the following numbers of engines for their plants in three cities.
The transportation costs per engine ($100s) from sources to destinations are shown in the following table. However, the Charlotte firm will not accept engines made in Seattle, and the Louisville firm will not accept engines from Detroit; therefore, these routes are prohibited.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14. | The Interstate Truck Rental firm has accumulated extra trucks at three of its truck leasing outlets, as shown in the following table.
The firm also has four outlets with shortages of rental trucks, as follows.
The firm wants to transfer trucks from those outlets with extras to those with shortages at the minimum total cost. The following costs of transporting these trucks from city to city have been determined.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15. | The Shotz Beer Company has breweries in two cities; the breweries can supply the following numbers of barrels of draft beer to the company's distributors each month.
The distributors, which are spread throughout six states, have the following total monthly demand.
The company must pay the following shipping costs per barrel.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16. | In problem 15, the Shotz Beer Company management has negotiated a new shipping contract with a trucking firm between its Tampa brewery and its distributor in Kentucky that reduces the shipping cost per barrel from $0.80 per barrel to $0.65 per barrel. How will this cost change affect the optimal solution? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17. | Computers Unlimited sells microcomputers to universities and colleges on the East Coast and ships them from three distribution warehouses. The firm is able to supply the following numbers of microcomputers to the universities by the beginning of the academic year.
Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year.
The shipping and installation costs per microcomputer from each distributor to each university are as follows.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18. | In problem 17, Computers Unlimited wants to better meet demand at the four universities it supplies . It is considering two alternatives: (1) expand its warehouse at Richmond to a capacity of 600 at a cost equivalent to an additional $6 in handling and shipping per unit, or (2) purchase a new warehouse in Charlotte that can supply 300 units with shipping costs of $19 to Tech, $26 to A and M, $22 to State, and $16 to Central. Which alternative should management select based solely on transportation costs (i.e., no capital costs)? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19. | Computers Unlimited in problem 17 has determined that when it is unable to meet the demand for microcomputers at the universities it supplies, the universities tend to purchase microcomputers elsewhere in the future. Thus, the firm has estimated a shortage cost for each microcomputer demanded but not supplied that reflects the loss of future sales and goodwill. These costs for each university are as follows:
Solve problem 17 with these shortage costs included. Compute the total transportation cost and the total shortage cost. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20. | A severe winter ice storm has swept across North Carolina and Virginia, followed by over a foot of snow and frigid, single-digit temperatures . These weather conditions have resulted in numerous downed power lines and power outages in the region causing dangerous conditions for much of the population. Local utility companies have been overwhelmed and have requested assistance from unaffected utility companies across the Southeast. The following table shows the number of utility trucks with crews available from five different companies in Georgia, South Carolina, and Florida; the demand for crews in seven different areas that local companies cannot get to; and the weekly cost ($1,000s) of a crew going to a specific area (based on the visiting company's normal charges, the distance the crew has to come, and living expenses in an area).
Determine the number of crews that should be sent from each utility to each affected area that will minimize total costs. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21. | A large manufacturing company is closing three of its existing plants and intends to transfer some of its more skilled employees to three plants that will remain open . The number of employees available for transfer from each closing plant is as follows.
The following number of employees can be accommodated at the three plants remaining open.
Each transferred employee will increase product output per day at each plant as shown in the following table. The company wants to transfer employees so as to ensure the maximum increase in product output.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22. | The Sav-Us Rental Car Agency has six lots in Nashville, and it wants to have a certain number of cars available at each lot at the beginning of each day for local rental. The agency would like a model it could quickly solve at the end of each day that would tell it how to redistribute the cars among the six lots in the minimum total time. The time required to travel between the six lots are as follows.
The agency would like the following number of cars at each lot at the end of the day. Also shown is the number of available cars at each lot at the end of a particular day. Determine the optimal reallocation of rental cars using any initial solution approach and any solution method.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23. | Bayville has built a new elementary school so that the town now has a total of four schoolsAddison, Beeks, Canfield, and Daley. Each has a capacity of 400 students. The school wants to assign children to schools so that their travel time by bus is as short as possible. The school has partitioned the town into five districts conforming to population densitynorth, south, east, west, and central. The average bus travel time from each district to each school is shown as follows.
Determine the number of children that should be assigned from each district to each school to minimize total student travel time. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24. | In problem 23, the school board has determined that it does not want any one school to be more crowded than any other school. It would like to assign students from each district to each school so that enrollments are evenly balanced between the four schools. However, the school board is concerned that this might significantly increase travel time. Determine the number of students to be assigned from each district to each school so that school enrollments are evenly balanced. Does this new solution appear to result in a significant increase in travel time per student? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25. | The Easy Time Grocery chain operates in major metropolitan areas on the eastern seaboard. The stores have a " no-frills " approach, with low overhead and high volume. They generally buy their stock in volume at low prices. However, in some cases they actually buy stock at stores in other areas and ship it in. They can do this because of high prices in the cities they operate in compared with costs in other locations. One example is baby food. Easy Time purchases baby food at stores in Albany, Binghamton, Claremont, Dover, and Edison, and then trucks it to six stores in and around New York City. The stores in the outlying areas know what Easy Time is up to, so they limit the number of cases of baby food Easy Time can purchase. The following table shows the profit Easy Time makes per case of baby food based on where the chain purchases it and which store it's sold at, plus the available baby food per week at purchase locations and the shelf space available at each Easy Time store per week.
Determine where Easy Time should purchase baby food and how the food should be distributed in order to maximize profit. Use any initial solution approach and any solution method. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26. | Suppose that in problem 25 Easy Time can purchase all the baby food it needs from a New York City distributor at a price that will result in a profit of $9 per case at stores 1, 3, and 4, $8 per case at stores 2 and 6, and $7 per case at store 5. Should Easy Time purchase all, none, or some of its baby food from the distributor rather than purchasing it at other stores and trucking it in? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27. | In problem 25, if Easy Time could arrange to purchase more baby food from one of the outlying locations, which should it be, how many additional cases could be purchased, and how much would this increase profit? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28. | The Roadnet Transport Company has expanded its shipping capacity by purchasing 90 trailer trucks from a competitor that went bankrupt. The company subsequently located 30 of the purchased trucks at each of its shipping warehouses in Charlotte, Memphis, and Louisville. The company makes shipments from each of these warehouses to terminals in St. Louis, Atlanta, and New York. Each truck is capable of making one shipment per week. The terminal managers have indicated their capacity of extra shipments. The manager at St. Louis can accommodate 40 additional trucks per week, the manager at Atlanta can accommodate 60 additional trucks, and the manager at New York can accommodate 50 additional trucks. The company makes the following profit per truckload shipment from each warehouse to each terminal. The profits differ as a result of differences in products shipped, shipping costs, and transport rates.
Determine how many trucks to assign to each route (i.e., warehouse to terminal) in order to maximize profit. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29. | During the Gulf War, Operation Desert Storm required large amounts of military mat riel and supplies to be shipped daily from supply depots in the United States to bases in the Middle East. The critical factor in the movement of these supplies was speed. The following table shows the number of planeloads of supplies available each day from each of six supply depots and the number of daily loads demanded at each of five bases. (Each planeload is approximately equal in tonnage.) Also included are the transport hours per plane, including loading and fueling, actual flight time, and unloading and refueling.
Determine the optimal daily flight schedule that will minimize total transport time. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30. | PM Computer Services produces personal computers from component parts it buys on the open market. The company can produce a maximum of 300 personal computers per month. PM wants to determine its production schedule for the first six months of the new year. The cost to produce a personal computer in January will be $1,200. However, PM knows the cost of component parts will decline each month such that the overall cost to produce a PC will be 5% less each month. The cost of holding a computer in inventory is $15 per unit per month. Following is the demand for the company's computers each month.
Determine a production schedule for PM that will minimize total cost. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31. | In problem 30, suppose the demand for personal computers increased each month as follows.
In addition to the regular production capacity of 300 units per month, PM Computer Services can also produce an additional 200 computers per month using overtime. Overtime production adds 20% to the cost of a personal computer. Determine a production schedule for PM that will minimize total cost. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32. | National Foods Company has five plants where it processes and packages fruits and vegetables. It has suppliers in six cities in California, Texas, Alabama, and Florida. The company has owned and operated its own trucking system in the past for transporting fruits and vegetables from its suppliers to its plants. However, it is now considering outsourcing all of its shipping to outside trucking firms and getting rid of its own trucks. It currently spends $245,000 per month to operate its own trucking system. It has determined monthly shipping costs (in $1,000s per ton) using outside shippers from each of its suppliers to each of its plants as shown in the following table.
Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33. | In problem 32, National Foods would like to know what the effect would be on the optimal solution and the company's decision regarding its shipping if it negotiates with its suppliers in Sacramento, Jacksonville, and Ocala to increase their capacity to 25 tons per month? What would be the effect of negotiating instead with its suppliers at San Antonio and Montgomery to increase their capacity to 25 tons each? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34. | Orient Express is a global distribution company that transports its clients ' products to customers in Hong Kong, Singapore, and Taipei. All of the products Orient Express ships are stored at three distribution centers, one in Los Angeles, one in Savannah, and one in Galveston. For the coming month the company has 450 containers of computer components available at the Los Angeles center, 600 containers available at Savannah, and 350 containers available in Galveston. The company has orders for 600 containers from Hong Kong, 500 containers from Singapore, and 500 containers from Taipei. The shipping costs per container from each U.S. port to each of the overseas ports are shown in the following table.
The Orient Express as the overseas broker for its U.S. customers is responsible for unfulfilled orders, and it incurs stiff penalty costs from overseas customers if it does not meet an order. The Hong Kong customers charge a penalty cost of $800 per container for unfulfilled demand, Singapore customers charge a penalty cost of $920 per container, and Taipei customers charge $1,100 per container. Formulate and solve a transportation model to determine the shipments from each U.S. distribution center to each overseas port that will minimize shipping costs. Indicate what portion of the total cost is a result of penalties. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35. | Binford Tools manufactures garden tools. It uses inventory, overtime, and subcontracting to absorb demand fluctuations. Expected demand, regular and overtime production capacity, and subcontracting capacity are provided in the following table for the next four quarters for its basic line of steel garden tools.
The regular production cost per unit is $20, the overtime cost per unit is $25, the cost to subcontract a unit is $27, and the inventory carrying cost is $2 per unit. The company has 300 units in inventory at the beginning of the year. Determine the optimal production schedule for the four quarters that will minimize total costs. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36. | Solve the following linear programming problem. subject to | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37. | A plant has four operators to be assigned to four machines. The time (minutes) required by each worker to produce a product on each machine is shown in the following table. Determine the optimal assignment and compute total minimum time.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38. | A shop has four machinists to be assigned to four machines. The hourly cost of having each machine operated by each machinist is as follows.
However, because he does not have enough experience, machinist 3 cannot operate machine B.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39. | The Omega pharmaceutical firm has five salespersons, whom the firm wants to assign to five sales regions. Given their various previous contacts, the salespersons are able to cover the regions in different amounts of time. The amount of time (days) required by each salesperson to cover each city is shown in the following table. Which salesperson should be assigned to each region to minimize total time? Identify the optimal assignments and compute total minimum time.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40. | The Bunker Manufacturing firm has five employees and six machines and wants to assign the employees to the machines to minimize cost. A cost table showing the cost incurred by each employee on each machine follows. Because of union rules regarding departmental transfers, employee 3 cannot be assigned to machine E and employee 4 cannot be assigned to machine B. Solve this problem, indicate the optimal assignment, and compute total minimum cost.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41. | Given the following cost table for an assignment problem, determine the optimal assignment and compute total minimum cost. Identify all alternative solutions if there are multiple optimal solutions.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42. | An electronics firm produces electronic components, which it supplies to various electrical manufacturers. Quality control records indicate that different employees produce different numbers of defective items. The average number of defects produced by each employee for each of six components is given in the following table. Determine the optimal assignment that will minimize the total average number of defects produced by the firm per month.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43. | A dispatcher for the Citywide Taxi Company has six taxicabs at different locations and five customers who have called for service. The mileage from each taxi's present location to each customer is shown in the following table. Determine the optimal assignment(s) that will minimize the total mileage traveled.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44. | The Southeastern Conference has nine basketball officials who must be assigned to three conference games , three to each game. The conference office wants to assign the officials so that the total distance they travel will be minimized. The distance (in miles) each official would travel to each game is given in the following table.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45. | In problem 44, officials 2 and 8 have had a recent confrontation with one of the coaches in the game in Athens. They were forced to eject the coach after several technical fouls. The conference office has decided that it would not be a good idea to have these two officials work the Athens game so soon after this confrontation, so they have decided that officials 2 and 8 will not be assigned to the Athens game. How will this affect the optimal solution to this problem? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46. | State University has planned six special catered events for the November Saturday of its homecoming football game. The events include an alumni brunch, a parent's brunch, a booster club luncheon, a postgame party for season ticket holders, a lettermen's dinner, and a fund-raising dinner for major contributors. The university wants to use local catering firms as well as the university catering service to cater these events and it has asked the caterers to bid on each event. The bids (in $1,000s) based on menu guidelines for the events prepared by the university are shown in the following table.
The Bon Apet t, Custom, and University caterers can handle two events, whereas the other four caterers can handle only one. The university is confident all the caterers will do a high-quality job, so it wants to select the caterers for the events that will result in the lowest total cost. Determine the optimal selection of caterers that will minimize total cost. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47. | A university department head has five instructors to be assigned to four different courses. All of the instructors have taught the courses in the past and have been evaluated by the students. The rating for each instructor for each course is given in the following table (a perfect score is 100). The department head wants to know the optimal assignment of instructors to courses that will maximize the overall average evaluation. The instructor who is not assigned to teach a course will be assigned to grade exams. Solve this problem using the assignment method.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48. | The coach of the women's swim team at State University is preparing for the conference swim meet and must choose the four swimmers she will assign to the 800-meter medley relay team. The medley relay consists of four strokesthe backstroke, breaststroke, butterfly , and freestyle. The coach has computed the average times (in minutes) each of her top six swimmers has achieved in each of the four strokes for 200 meters in previous swim meets during the season as follows.
Determine the medley relay team and its total expected relay time for the coach. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49. | Biggio's Department Store has six employees available to assign to four departments in the store home furnishing , china, appliances, and jewelry . Most of the six employees have worked in each of the four departments on several occasions in the past, and have demonstrated that they perform better in some departments than in others. The average daily sales for each of the six employees in each of the four departments is shown in the following table.
Employee 3 has not worked in the china department before, so the manager does not want to assign this employee to china. Determine which employee to assign to each department and indicate the total expected daily sales. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50. | The Vanguard Publishing Company has eight college students it hires as salespeople to sell encyclopedias during the summer. The company desires to allocate them to three sales territories. Territory 1 requires three salespeople, and territories 2 and 3 require two salespeople each. It is estimated that each salesperson will be able to generate the amounts of dollar sales per day in each of the three territories as given in the following table. The company desires to allocate the salespeople to the three territories so that sales will be maximized. Solve this problem using any method to determine the initial solution and any solution method. Compute the maximum total sales per day.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51. | Carolina Airlines, a small commuter airline in North Carolina, has six flight attendants whom it wants to assign to six monthly flight schedules in a way that will minimize the number of nights they will be away from their homes . The numbers of nights each attendant must be away from home with each schedule are given in the following table. Identify the optimal assignments that will minimize the total number of nights the attendants will be away from home.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52. | The football coaching staff at Tech focuses its recruiting on several key states, including Georgia, Florida, Virginia, Pennsylvania, New York, and New Jersey. The staff includes seven assistant coaches, two of whom are responsible for Florida, a high school talent-rich state, whereas one coach is assigned to each of the other five states. The staff has been together for a long time and at one time or another all the coaches have recruited all of the states. The head coach has accumulated some data on the past success rate (i.e., percentage of targeted recruits signed) for each coach in each state as shown in the following table.
Determine the optimal assignment of coaches to recruiting regions that will maximize the overall-success rate and indicate the average percentage success rate for the staff with this assignment. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EAN: 2147483647
Pages: 358