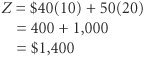A Maximization Model Example | Introduction to Management Science (10th Edition)

[Page 30 ( continued )]

Beaver Creek Pottery Company is a small crafts operation run by a Native American tribal council. The company employs skilled artisans to produce clay bowls and mugs with authentic Native American designs and colors. The two primary resources used by the company are special pottery clay and skilled labor. Given these limited resources, the company desires to know how many bowls and mugs to produce each day in order to maximize profit. This is generally referred to as a product mix problem type. This scenario is illustrated in Figure 2.1.

[Page 31]

Time Out: For George B. Dantzig

Linear programming, as it is known today, was conceived in 1947 by George B. Dantzig while he was the head of the Air Force Statistical Control's Combat Analysis Branch at the Pentagon. The military referred to its plans for training, supplying, and deploying combat units as "programs." When Dantzig analyzed Air Force planning problems, he realized that they could be formulated as a system of linear inequalitieshence his original name for the technique, "programming in a linear structure," which was later shortened to "linear programming."

Figure 2.1. Beaver Creek Pottery Company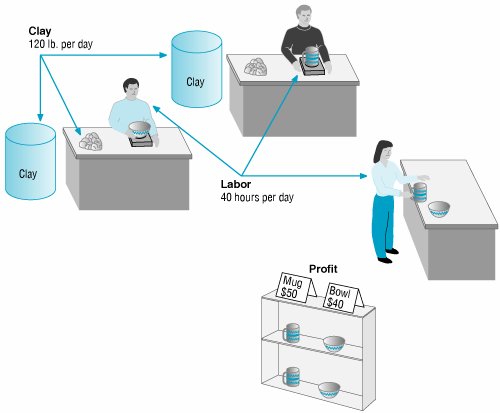

The two products have the following resource requirements for production and profit per item produced (i.e., the model parameters):

	Resource Requirements
Product	L ABOR ( HR./UNIT )	C LAY ( LB./UNI t)	P ROFIT ( $/UNIT )
Bowl	1	4	40
Mug	2	3	50

[Page 32]

There are 40 hours of labor and 120 pounds of clay available each day for production. We will formulate this problem as a linear programming model by defining each component of the model separately and then combining the components into a single model. The steps in this formulation process are summarized as follows :

Summary of LP Model Formulation Steps

Step 1.	Define the decision variables How many bowls and mugs to produce
Step 2.	Define the objective function Maximize profit
Step 3.	Define the constraints The resources (clay and labor) available

A linear programming model consists of decision variables, an objective function, and constraints.

Decision Variables

The decision confronting management in this problem is how many bowls and mugs to produce. The two decision variables represent the number of bowls and mugs to be produced on a daily basis. The quantities to be produced can be represented symbolically as

x ₁ = number of bowls to produce

x ₂ = number of mugs to produce

The Objective Function

The objective of the company is to maximize total profit. The company's profit is the sum of the individual profits gained from each bowl and mug. Profit derived from bowls is determined by multiplying the unit profit of each bowl, $40, by the number of bowls produced, x ₁ . Likewise, profit derived from mugs is derived from the unit profit of a mug, $50, multiplied by the number of mugs produced, x ₂ . Thus, total profit, which we will define symbolically as Z , can be expressed mathematically as $40 x ₁ + $50 x ₂ . By placing the term maximize in front of the profit function, we express the objective of the firmto maximize total profit:

maximize Z = $40 x ₁ + 50 x ₂

where

Z	=	total profit per day
$40 x ₁	=	profit from bowls
$50 x ₂	=	profit from mugs

Model Constraints

In this problem two resources are used for productionlabor and clayboth of which are limited. Production of bowls and mugs requires both labor and clay. For each bowl produced, 1 hour of labor is required. Therefore, the labor used for the production of bowls is 1 x ₁ hours. Similarly, each mug requires 2 hours of labor; thus, the labor used to produce mugs every day is 2 x ₂ hours. The total labor used by the company is the sum of the individual amounts of labor used for each product:

1 x ₁ + 2 x ₂

[Page 33]

However, the amount of labor represented by 1 x ₁ + 2 x ₂ is limited to 40 hours per day; thus, the complete labor constraint is

1 x ₁ + 2 x ₂ 40 hr.

The "less than or equal to" ( ) inequality is employed instead of an equality (=) because the 40 hours of labor is a maximum limitation that can be used , not an amount that must be used . This constraint allows the company some flexibility; the company is not restricted to using exactly 40 hours but can use whatever amount is necessary to maximize profit, up to and including 40 hours. This means that it is possible to have idle, or excess, capacity (i.e., some of the 40 hours may not be used).

The constraint for clay is formulated in the same way as the labor constraint. Because each bowl requires 4 pounds of clay, the amount of clay used daily for the production of bowls is 4 x ₁ pounds; and because each mug requires 3 pounds of clay, the amount of clay used daily for mugs is 3 x ₂ . Given that the amount of clay available for production each day is 120 pounds, the material constraint can be formulated as

4 x ₁ + 3 x ₂ 120 lb.

A final restriction is that the number of bowls and mugs produced must be either zero or a positive value because it is impossible to produce negative items. These restrictions are referred to as nonnegativity constraints and are expressed mathematically as

Nonnegativity constraints restrict the decision variables to zero or positive values.

x ₁ 0, x ₂

The complete linear programming model for this problem can now be summarized as follows:

The solution of this model will result in numeric values for x ₁ and x ₂ that will maximize total profit, Z . As one possible solution, consider x ₁ = 5 bowls and x ₂ = 10 mugs. First, we will substitute this hypothetical solution into each of the constraints in order to make sure that the solution does not require more resources than the constraints show are available:

and

Because neither of the constraints is violated by this hypothetical solution, we say the solution is feasible (i.e., it is possible). Substituting these solution values in the objective function gives Z = 40(5) + 50(10) = $700. However, for the time being, we do not have any way of knowing whether $700 is the maximum profit.

A feasible solution does not violate any of the constraints .

Now consider a solution of x ₁ = 10 bowls and x ₂ = 20 mugs. This solution results in a profit of

[Page 34]

Although this is certainly a better solution in terms of profit, it is infeasible (i.e., not possible) because it violates the resource constraint for labor:

An infeasible problem violates at least one of the constraints.

The solution to this problem must maximize profit without violating the constraints. The solution that achieves this objective is x ₁ = 24 bowls and x ₂ = 8 mugs, with a corresponding profit of $1,360. The determination of this solution is shown using the graphical solution approach in the following section.