SUM OR DIFFERENCE OF TWO RANDOM VARIABLES: X1 AND X2

SUM OR DIFFERENCE OF TWO RANDOM VARIABLES: X ₁ AND X ₂

Y = a ₁ X ₁ ± a ₂ X ₂

Mean: ¼ _Y = a ₁ ¼ _X1 ± a ₂ ¼ _X2

Variances: ƒ ² _Y = a ₁ ² ƒ ² _X1 + a ₂ ² ƒ ² _X2 ± a ₁ a ₂ ƒ ² _X1X2

Where Covariance: ƒ ² _X1X2 = 0, if independent

Problem: Number of people in car pool

Experiment: Observe 20 consecutive cars in "HOV" lane

Assumption: Population is infinite

Find: Central tendencies and dispersions

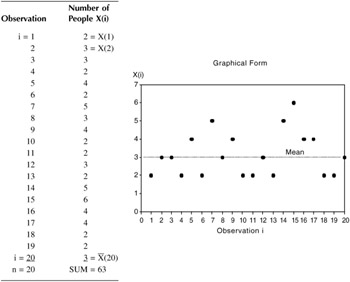
Mean of observed data: (use sub i for individual sample)

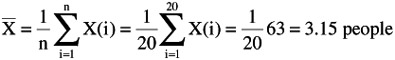
You should not expect the mean to equal an observable value, e.g., 3.