2.2 Twisted Pair Cable Channel Model

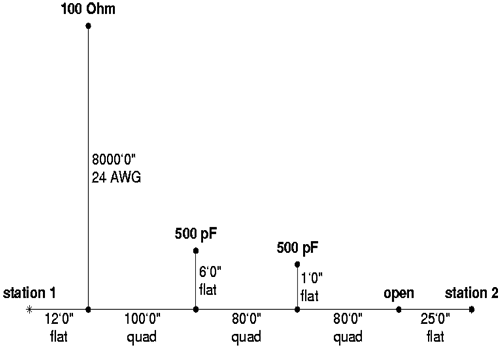
2.2.1 Wiring Topology

In an office environment, twisted pair cables are wired from each desk to a central location, usually a dedicated wiring closet, where an Ethernet hub is used to connect every incoming cable at the center of a star. This is often called a star wiring configuration. Under this star wiring configuration, a straight twisted cable is used between a port of the hub and a computer NIC. With ideal terminations at both ends of a twisted pair cable, the transfer function of the twisted pair based transmission channel can be estimated accurately using its propagation constant (Equation 2.8 or 2.9) for an identified distance. The star wiring configuration can also be found in some residences, especially in some newly constructed residential areas where the awareness of data transmission within a household exists. In a majority of existing residential premises, however, twisted pair telephone cables are wired following a daisy-chain fashion. For example, from the NID (Network Interface Device), one twisted pair cable connects a few telephone jacks on the first floor, and a second one connects all phone jacks on the second floor. The homeowner may have added another twisted pair cable to connect the computers, fax machines, and other auxiliary devices at a few different places.

The star daisy-chain telephone in-house wiring configuration in Figure 2.3 shows four phone jacks in this residential premises [6]. The jacks at both ends are marked as station 1 and station 2. Each of the other two are terminated with a capacitor of 500 picofarads (pF) representing an on-hook telephone set. The Central Office is represented by a 100-ohm load at 8000 ft. For this general star daisy-chain wiring configuration, we need to know two-port network representation of all cable sections as well as terminations to estimate the transfer function.

Figure 2.3. An Example of a Telephone Wiring Configuration

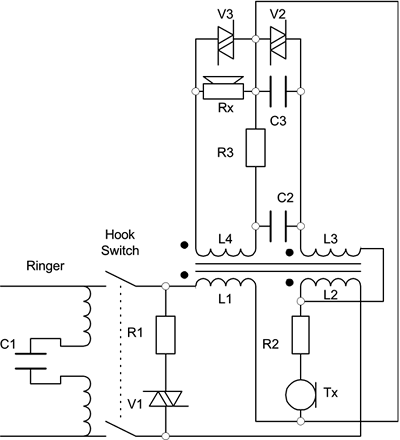
2.2.2 Telephony Devices

A telephone set is often called POTS (Plain Old Telephone Set) in telecommunications jargon. All telephone sets have followed the original Bell Systems' 500/2500 series design, but integrated electronics have replaced some more expensive electromechanical and special-purpose devices. The general circuit diagram of a 500/2500 telephone set is shown in Figure 2.4 [7]. A telephone set consists of a ringer, which is always connected to the telephone loop, a transmitter (microphone) or Tx, a receiver (ear piece) or Rx, and a single transformer based balance network. The dial is omitted for simplicity. There are three varistors in a typical 500/2500 series telephone set. (A varistor is an electrical component whose resistance varies according to its bias current.)

Figure 2.4. Schematics of a Typical (500) Telephone Set

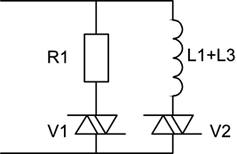
Varistor V1 is used to compensate loop length differences. A smaller resistance of V1 under a short loop, and therefore a high bias current, results in a higher signal loss. Varistor V2 is used for automatic side tone (self-echo) strength adjustment so that talkers can feel the liveliness of their own speech at a certain level, while V3 is used to limit the signal from a pulse or tone dialer. For the broadband home networking over the in-house wiring, POTS presents only a termination impedance. From that perspective, the POTS circuit can be simplified to either a ringer, which is represented by a capacitance of about 500 pF because of the distributed capacitances of the ringer coil or the equivalent electronics at high frequencies, or the ringer plus an impedance consisting of nonlinear varistors, a resistor, and an inductor as shown in Figure 2.5. Zener diodes have been used in place of varistors for recently manufactured telephone sets. As long as the broadband signal is low in amplitude, the equivalent circuit of a telephone set is pretty much linear and representable by the 500-pF capacitor.

Figure 2.5. A Simplified POTS Equivalent Circuit

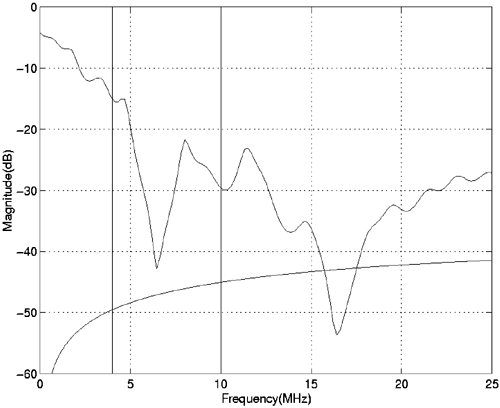
Figure 2.6 shows the insertion loss (which is very similar to but a more accurate representation of transfer function) of the example star daisy-chain wiring configuration of Figure 2.3 from station 1 to station 2 with the effects of wiring interconnections and terminations all included. The lower smooth curve also in Figure 2.6 is the corresponding crosstalk loss between adjacent twisted pairs. The insertion loss is estimated by first calculating ABCD parameters of each cable section and termination as a two-port network and then the overall ABCD parameters of the circuit network between station 1 and station 2. As is shown later in this section, the use of ABCD parameters is a convenient way of describing input-to-output current and voltage relationships. The insertion loss is then calculated based on the overall ABCD parameters. Two deep notches in Figure 2.6 around 7 and 16.5 MHz are caused by reflections of different cable branches and mismatched terminal impedances.

Figure 2.6. Insertion Loss of a Telephone Wiring

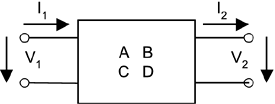
2.2.3 Two-Port Network and ABCD Parameters

The twisted pair cable transfer function based on the propagation constant, H(d,f) = e^-da(f) e^-jdb(f), is only good for a single-gauge twisted pair with ideal terminations at both ends. In-house telephone wiring, however, usually consists of many twisted pair cables connected in a star daisy-chain fashion, with ends that are either open or terminated with telephony devices of nonideal impedances. To represent accurately an in-house wiring transfer function from one phone jack to another, a two-port network and its ABCD parameter representation are used in calculation.

An electronic circuit is usually designed for analog filtering or digital processing of signals between its input port and output port. The function of the electronic circuit is to produce a desired output signal based on certain input signals. A twisted pair cable section or a twisted pair telephone subscriber loop can also be viewed as having an input port where a signal arrives and an output port where the signal leaves. The function of an electronic circuit or the transfer function of a twisted pair telephone loop can be determined solely according to its input/output current/voltage relationships. Figure 2.7 shows the model of a two-port network, which can represent an electronic circuit or a twisted pair telephone cable. V₁ and I₁ are input port voltage and current, respectively. V₂ and I₂ are output port voltage and current, respectively. Input port voltage and current and output port voltage and current are related by ABCD parameters of the two-port network. Note that ABCD parameters are generally not constants but rather frequency-dependent complex variables.

Figure 2.7. A Two-Port Network

For a stand-alone two-port network, the input and output voltage and current relationship is represented as

Equation 2.11

Equation 2.12

or in matrix format as

Equation 2.13

where these ABCD parameters are defined as

ABCD parameters for a simple two-port network consisting of a series impedance as shown in Figure 2.8 can be derived as follows. We have

Figure 2.8. A Series Impedance as a Two-Port Network

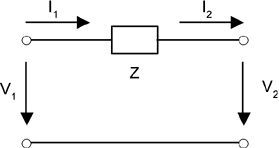
Therefore, the ABCD parameter matrix for a series impedance Z as a two-port network is as follows:

Equation 2.14

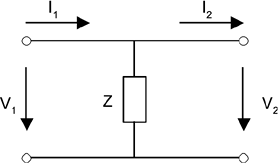
ABCD parameters for another simple two-port network consisting of a shunt impedance as shown in Figure 2.9 can be derived as follows. We have

Figure 2.9. A Shunt Impedance as a Two-Port Network

Therefore, the ABCD parameter matrix for a shunt impedance Z as a two-port network is

Equation 2.15

ABCD parameters of a twisted pair cable are complex and frequency-dependent. They are related to characteristic impedance, Z₀(s), and propagation constant, g(s), as

Equation 2.16

Equation 2.17

Equation 2.18

where d is the length of the twisted pair cable.

Many electronic circuits can be divided into a few simpler two-port networks. These simpler two-port networks are usually connected either in series or in parallel. A twisted pair telephone loop consists of many twisted pair cables in series. The use of twisted pair ABCD parameters is convenient because each section of a twisted pair subscriber loop can be described by its own ABCD parameters, and the ABCD parameters of the whole subscriber loop are the matrix product of individual ABCD matrices.

To obtain the ABCD parameters of two two-port networks in series, equate the output port voltage and current of the first two-port network to the input port voltage and current of the following network, as shown in Figure 2.10, and then derive the relationship between the input port voltage and current of the first two-port network to the output port voltage and current of the following network.

Figure 2.10. Two Two-Port Networks in Serial

For two two-port networks in series, the input and output voltage and current relationship is represented as

Equation 2.19

Equation 2.20

and

Equation 2.21

Therefore, the ABCD parameter matrix for two two-port networks in series is

Equation 2.22

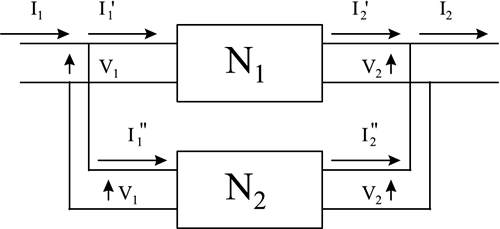
We can obtain the ABCD parameters of two two-port networks in parallel by equating the input port voltages of these two-port networks and the output port voltages of these two-port networks as shown in Figure 2.11 and deriving the relationship between input port voltage and the combined input current and output port voltage and the combined output current of these two two-port networks.

Figure 2.11. Two Two-Port Networks in Parallel

The voltage and current relationships of two two-port networks in parallel are represented as

Equation 2.23

Equation 2.24

Equation 2.25

Equation 2.26

Combining V₁ = A₁V₂ + B₁I₂' and V₁ = A₂V₂ + B₂I₂" results in

Equation 2.27

We also have

Equation 2.28

which can be expressed as

Equation 2.29

or

Equation 2.30

by using

Equation 2.31

Combining these two expressions results in

Equation 2.32

Therefore, the ABCD parameter matrix for two two-port networks in parallel is

Equation 2.33

The special case of two identical two-port networks in parallel is represented as

Equation 2.34

Equation 2.35

Equation 2.36

Equation 2.37

where A, B, C, and D are ABCD parameters of each individual two-port network and A_p, B_p, C_p, and D_p are ABCD parameters of two two-port networks in parallel.

2.2.4 Impedance, Transfer Function, and Insertion Loss

The ABCD matrix information of a twisted pair telephone loop can be easily converted into its input impedance or transfer function. Corresponding calculations can be put into a computer program [8] to generate channel models in conjunction with a few tables of twisted pair cable primary parameters.

The input impedance of a twisted pair loop with a terminal impedance of Z_t(s) is expressed as

Equation 2.38

where A(s), B(s), C(s), and D(s) are complex frequency-dependent ABCD parameters of a twisted pair telephone cable. When the other end of the twisted pair cable is left open, we have

Equation 2.39

This is also the impedance of a twisted pair cable branch with an open-end. An open-ended cable branch can be considered as a two-port network with only a shunt impedance. Therefore, the ABCD parameters of an open-ended branch are as follows:

Equation 2.40

where A_branch(s), and C_branch(s) are parts of frequency-dependent ABCD parameters of the open-ended cable branch.

The transfer function of a twisted pair loop with a source impedance of Z_s(s) and a terminal impedance of Z_t(s) is

Equation 2.41

When the effect of source impedance is excluded, that is, Z_s(S) = 0 , we have

Equation 2.42

Following earlier practices of the Bell System [9], the insertion loss, which is defined as

Equation 2.43

has been used as the channel model for DSL system performance simulation studies. By using insertion loss, we avoid the signal loss caused by the voltage division between source and loop input impedances while still including the effect of the source impedance or the voltage division between source and termination impedances when the loop is very short. For an example of a zero length or null loop, that is, for

Equation 2.44

the transfer function is

Equation 2.45

while the insertion loss is

Equation 2.46

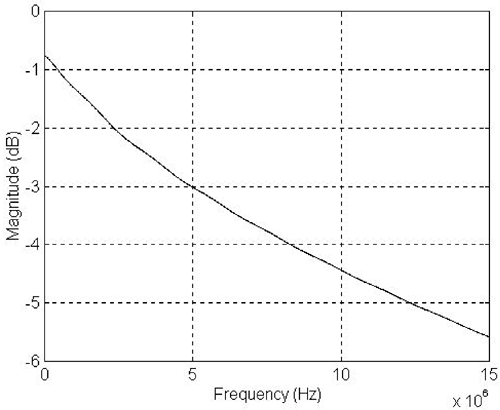
The insertion loss more accurately represents the effect of a twisted pair cable inserted between the source and the termination.

The insertion loss of in-house wiring can be studied in terms of wire loss, branch loss, and reflection loss. Wire loss is relatively insignificant when it is compared with those losses caused by branching and reflection. While the branch loss is related to the number of branches, the reflection loss-caused notch is related to the cable length of the branch. An average-size two-storey house has a dimension of 20 ft (height) by 30 ft (width) and by 40 ft (length). The summation of all house dimensions is therefore 90 ft. With the consideration of some additional routing length, Figure 2.12 shows the insertion loss of a 150-ft flat 26-gauge telephone in-house wire.

Figure 2.12. Insertion Loss of a 26-Gauge 150-ft Flat Wire

The insertion loss is less than 5 dB below 12 MHz. Figure 2.13 shows the insertion loss of a 150-ft flat 26-gauge telephone in-house wire and insertion losses of those in conjunction with one, two, three, and four flat 26-gauge in-house wire branches that are 15,000 ft. Long-length branches are used to show the effects of branching only.

Figure 2.13. A 150-ft Flat 26-Gauge Flat Wire with Long Branches

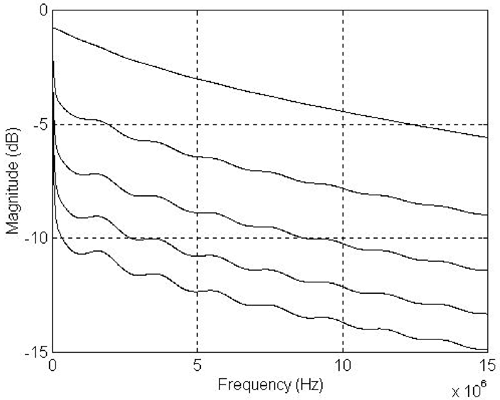
Compared with the insertion loss without any branch, each additional long cable branch causes additional energy loss of between 2 and 3 dB. The amount of branch loss approximately represents power-sharing factors of 2, 3, 4, and 5. Figure 2.14 shows insertion loss of a 26-gauge 150-ft twisted pair cable as well as insertion losses of those with an in-house wiring branch of 10, 20, and 30 ft.

Figure 2.14. A 150-ft 26-Gauge Flat Wire with 15-ft Branches

Compared with the insertion loss without any branch, a 30-ft cable branch causes the lowest frequency notch at around 4.8 MHz and the second frequency notch at around 14.5 MHz. On the other hand, the first frequency notch of a 10-ft in-house wiring branch is also at around 14.5 MHz. The frequency notch is caused by reflections from a branch with a 180-degree phase shift. In other words, the first frequency notch is the result of the reflection from the branch with a half-wave delay, the second frequency notch is the result of a one-and-a-half wave delay, and so on. The location of a notch frequency can be estimated based on branch length according to the following expression:

Equation 2.47

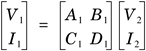
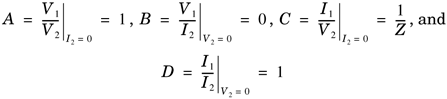
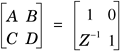
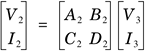
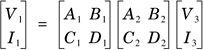
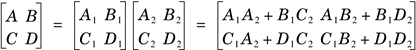
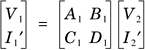
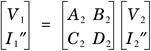
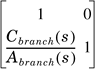
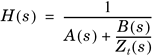
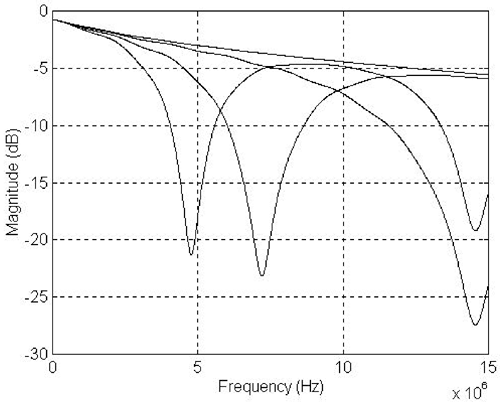
where f_i is the ith frequency notch, l is the branch length, and c is the speed of transmission over the in-house wiring. We have c 5.8 x 10⁸ feet per second (ft/sec). With that transmission speed, we can estimate that the first frequency notch corresponding to a 20-ft branch is at around 7.25 MHz.