Hack 21. Choose the Honest Average

Data-driven decisions, such as whether you can afford to buy a house in a new town or who the core market is for your business, often rely on the "average" as the best description for a large set of data. The problem is that there are three completely different values that can be labeled as the "average," and the different averages often result in different decisions. Make your decisions using the correct average.

When most people hear a statement like "the average price for a house in this town is $290,000" (which might sound low, high, or just right, depending on where you call home), they imagine that this figure was determined by adding up all of the sales prices from all of the houses in the town, and then dividing that sum by the number of houses. But statisticians know there is more than one way to determine the "average," and sometimes one kind is better than another.

Whether that $290,000 really represents the typical housing price depends on whether the average is actually the mean, median, or mode. It also depends on the shape of the distribution of all the numbers that are averaged. Wise folks will make sure they are making their decisions using the best summary value. Here's when to trust each type of average.

Measures of Central Tendency

The purpose of determining an average for a set of valueswhether those values are house prices, grades from a final exam, or the number of students in a yoga classis to efficiently communicate the central tendency for those values. It's true that, most of the time, central tendency is determined by adding up all of the values in a distribution, and then dividing the sum by the number of values. Statisticians don't call this the average, though; they call it the mean. So, why not always use the mean to determine central tendency? Because in some situations, the mean doesn't represent any of the actual values!

Consider the opening example about the average price of a house. Let's say you collect data for 300 houses in a town and want to determine the average sales price in that sample. Generally speaking, the mean is not a very good indicator of central tendency for house prices. Figure 2-5 illustrates why.

Figure 2-5. Mean as a misleading average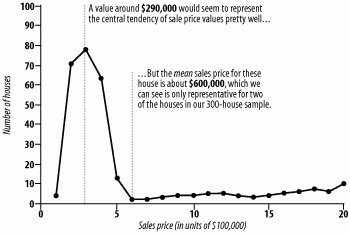

The mean is not a very honest average in this situation, because the distribution of sales prices is skewed by a few outlying values that are very large. Of the 300 houses sampled, 231 of them were sold for prices in between $100,000 and $600,000. The remaining 69 houses sold for prices above $600,000, with 56 of those above a million dollars. The mean is heavily influenced by these outlying values and therefore is not very representative of any house in the sample.

Means don't work well as averages for most money variables. The average income reported as a mean is much higher than what most people earn. There are always a few Bill Gates and J.K. Rowling types who pull the mean way up.

So, what's the "honest average" for these types of values? Instead of reporting the mean, with distributions like the one in Figure 2-5, honest statisticians generally prefer the median. The median is that value in a distribution at the 50th percentile, such that half of all values are below it and the other half are above it (just like, on a highway, the median divides the road in half). The median for this distribution of data is just under $290,000, and thus works very well as a measure of central tendency.

Choosing the Middle Ground

The median works well in these instances because it is much less sensitive to outlying values than the mean, and thus is preferred whenever a distribution is skewed in one direction or another. The median is therefore also the most "honest" measure of central tendency when the distribution is skewed by a few outlying values that are much smaller than the rest, as in Figure 2-6, a fictional set of 50 students' exam scores.

Figure 2-6. Median as the honest measure of central tendency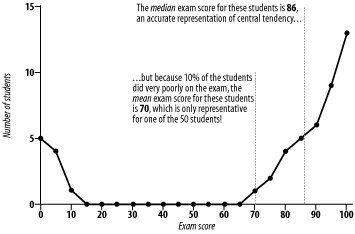

Figure 2-6 shows another type of data in which a mean might lead to a wrong conclusion. Relying on the median here would result in a more accurate interpretation of class performance.

Where It Doesn't Work

Not even the median will always be honest, though. Consider the following scenario. Say you're a yoga instructor, and half of the students in your class are between 25 and 35 years old, and the other half are between 50 and 60. How would you describe the average age of your students?

The problem in situations like these is that neither the mean nor the median will adequately describe the group of individuals. What to do? The most honest choice for an average in this situation is to report the mode, which is simply the most frequently occurring value in a sample of data, as shown in the example in Figure 2-7.

Figure 2-7. Mode as the honest average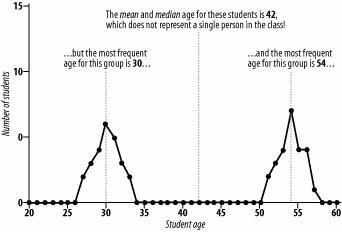

In this case, there are two modes: one at 30 years old and the other at 54 years old. Reporting both of these values is the best way to choose the honest average. The mean and median both mislead for these sorts of data.

How to Choose the Honest Average

So, when is the mean the honest average? Basically, the mean is the best choice when there is only one mode and the distribution is symmetric, which means that there is no obvious skew in either direction. If your yoga class were attended by your 25- to 35-year-old students only, the mean would be the honest average.

When all is said and done, how do you choose the most appropriate average? Following these three simple rules will keep you honest if you are reporting summaries, and will help you make informed choices if you are the one making decisions based on the data:

• Choose the mode if there are two or more "trends" in the data (i.e., two or more areas of high-frequency values), and report one mode for each trend.

• Choose the median if the distribution is skewed (i.e., a small number of outliers is heavily influencing the mean).

• Choose the mean if the distribution is fairly symmetric with one mode.

It is interesting to note that in most cases, the mean, the median, and the mode will all be fairly close to equal. So why bother with the mean? The mean remains as the most common way to report the average because it is most likely to be replicated if we were to take another sample of data and look for the central tendency. Medians and modes tend to be a lot more variable, but the mean stays nice and stable.

William Skorupski