Quantifying and Analyzing Activity Risks

Overview

"When you know a thing, to hold that you know it, and when you do not know a thing, to allow that you do not know it—this is knowledge."

—CONFUCIUS

Project planning processes serve several purposes, but probably the most important for risk management is to separate the parts of the work that are well understood, and therefore less risky, from the parts that are less well understood. Often, what separates an impossible project from a possible one is isolating the most difficult work early so that it receives the attention and effort it requires. Risk assessment techniques are central to gaining an understanding of what is most uncertain about a project, and they are the foundation for managing risk.

Most of the content of this chapter falls into the "Qualitative Risk Analysis" and "Quantitative Risk Analysis" portions of the Planning Processes in the PMBOK Guide. The focus of this chapter is analysis and prioritization of the identified project risks. Analysis of overall project risk is addressed in Chapter 9. The principal ideas in this chapter include:

• Risk probability assessment
• Risk impact assessment
• Risk matrices and tables
• PERT
• Decision trees

Quantitative and Qualitative Risk Analysis

Risk analysis strives for deeper understanding of potential project problems. Techniques for doing this effectively may provide either quantitative estimates and measures for each risk or qualitative information that places risks into ranges and categories.

Qualitative techniques are easier to apply and generally require less effort. Qualitative risk assessment is often sufficient for rank-ordering risks, allowing you to select the most significant ones for application of the management techniques discussed in Chapter 8.

Quantitative methods strive for greater precision, and they reveal more about each risk. These methods require more work, but, in addition to allowing you to sequence the risks from most to least significant, quantitative analysis also provides data you can use to assess overall project risk and to estimate schedule and/or budget reserves for risky projects.

Although the dichotomy between these approaches is explicit in the PMBOK Guide, analysis methods fall into a continuum of possibilities. They range from qualitative assessment using a small number of categories, through methods that use progressively more and finer distinctions, to the extreme of determining specific quantitative data for each risk. If the primary goal of risk analysis is to prioritize risks to determine which ones are important enough to warrant responses, the easiest qualitative assessment methods may suffice. If you need to assess project-level risk with maximum precision, then you will need to use quantitative assessment methods (though the nature of the available data usually puts a rather modest limit on the accuracy you can attain).

Whatever assessment method you apply, the foundation is always the same simple formula discussed in Chapter 1: "loss" multiplied by "likelihood." The realm of "likelihood" is statistics and probability, domains that many project contributors find confusing and at times counterintuitive. "Loss" in projects is measured in impact: time, money, and related project factors. These two parameters characterize risk, and both must be assessed for each project risk identified.

Risk Probability

The "likelihood," or probability, of a single event is always somewhere between zero (no chance of occurrence) and one (inevitable occurrence). Looking backward from the end of a project, every risk has one of these two values; it either happened or it did not. At the beginning of the project, though, there is uncertainty, and it is logical to assign a value somewhere in between. Qualitative risk assessment methods divide the choices into ranges and require project team members to assign each risk to one of the defined ranges. Quantitative risk assessment assigns each risk a specific fraction between zero and one (or between zero and 100 percent).

By definition, all probabilities fall within this range, but determining what value between zero and one to assign a given risk is often difficult. There are only three ways in practice to set probabilities. For some situations, such as flipping coins and throwing dice, mathematical analysis permits calculation of the expected probabilities. In other situations, a simple model does not exist, but there are many historical events that are sufficiently similar, and empirical data may be used for prediction; this is the basis of the insurance industry. In all other cases, probabilities are basically set by guessing. For complex events that occur seldom, perhaps even never (at least, not yet), you can neither calculate nor measure to determine a probability, so ideas such as referencing analogous situations, scenario analysis, and "gut feel" come into play. For most project risk situations, probabilities fall into the third category and therefore tend to be inexact.

Qualitative methods recognize this lack of precision and do not require specific numerical values. They divide the complete range into two or more nonoverlapping ranges or segments. The simplest qualitative assessment uses two ranges, "more likely than not (.5 to 1)" and "less likely than not (0 to .4999)." Most project teams are able to select one of these choices for each risk with little difficulty, but the coarse granularity of the analysis makes selecting significant risks for further attention fairly arbitrary.

A more common method for qualitative assessment uses three ranges, assigning a value of high, medium, or low to each risk. The definitions for these categories vary, but usually they are:

• High = 50 percent or higher (Likely)
• Medium = Between 10 and 50 percent (Unlikely)
• Low = 10 percent or lower (Very unlikely)

These three levels of probability are quickly and easily determined for risks without undue debate, and the resulting characterization of risk allows you to discriminate adequately between significant and trivial risks.

Other methods use four, five, or more categories. These methods tend to use linear ranges for the probabilities: quartiles for four, quintiles for five, and so forth. (The names assigned to five categories might be: very high, high, moderate, low, and very low.) The more ranges there are, the better the characterization of risk, but the harder it is for the project team to arrive at consensus.

The logical extension of this continues through assessments using integer percentages (one hundred categories) to continuous estimates that allow fractional percentages. While the apparent precision improves, the process for determining numerical probabilities may require a lot of overhead, and the data generated are still based primarily on guesses. The illusion of precision can be a source of risk in itself; avoid making subjective information look objective by inappropriate application of quantitative techniques.

Depending on the project, the quality of data available, and the planned uses for risk data, one (or more) of these assessment regimes can generate data on probability. For qualitative assessment methods using five or fewer categories, experience, polling, interviewing, or rough analysis of the risk situation is enough. For quantitative methods, a solid base of historical performance data is the best source, as it provides an empirical foundation for probability assessment. Estimating probabilities using methods such as the Delphi technique (discussed in Chapter 4), computer modeling (discussed later in this chapter), and use of knowledgeable experts (who may have access to much more data than you do) can also potentially improve the quality of quantitative probabilities.

Measurement-based probabilities, when possible, also serve a secondary purpose in project risk management: trend analysis. In hardware projects, statistics for component failure support decisions to retain or replace suppliers for future projects. If custom circuit boards, specialized integrated circuits, or other hardware components are routinely required on projects, quarter-by-quarter or year-by-year data across a number of projects will provide the fraction of components that are not accepted and provide data on whether process changes are warranted to improve the yields and success rates. Managing risk over the long term relies heavily on metrics, which are discussed in more detail in Chapter 9.

Risk Impact

The "loss," or project impact, for an individual risk is not as easily defined as the probability. The minimum is zero, but both the units and the maximum value are specific to the risk. The impact of a given risk may be relatively easy to ascertain and have a single, predictable value, or it may be best expressed as a distribution or histogram of possibilities. Qualitative risk assessment methods for impact again divide the choices into ranges, and the project team assigns each risk to a category on the basis of the magnitude of the risk consequences. For quantitative risk assessment, impact is estimated using units such as days of project slip, money, or some other suitable measure.

Qualitative assessment assigns each risk to one of two or more nonoverlapping categories. A two-range version uses categories such as "low severity" and "high severity," with suitable definitions of these terms related to attaining the project objective. As with probability analysis, the usefulness of only two categories is limited.

Discrimination is improved if you use three ranges, where each risk is assigned a value of high, medium, or low. The definitions for these categories vary, but commonly they relate to the project objective and plan as follows:

• High = Project objective is at risk (mandatory change to one or more of scope, schedule, and resources).
• Medium = Project objectives are okay, but significant replanning is required.
• Low = No major plan changes; the risk is an inconvenience or it will be handled through minor overtime work.

These three levels of project impact are not difficult to assess for most risks and provide fairly good data for sequencing risks according to severity.

Other methods use additional categories, and some partition impact further into specific project factors, such as schedule, cost, and scope. Impact measurement is open-ended; there is no theoretical maximum for any of these parameters (in a literally impossible project, time and cost may be thought of as infinite). Because the scale is not bounded, the categories used for impact are usually geometric, with small ranges at the low end and progressively larger ranges in the upper categories. For an impact assessment that uses five categories, definitions might be:

• Very low = Less than 1 percent impact on scope, schedule, cost, or quality
• Low = Less than 5 percent impact on scope, schedule, cost, or quality
• Moderate = Less than 10 percent impact on scope, schedule, cost, or quality
• High = Less than 20 percent impact on scope, schedule, cost, or quality
• Very high = 20 percent or more impact on scope, schedule, cost, or quality

Risks are assigned to a category on the basis of the expected variance of the most significant project parameter, so a risk that represents a 10 percent schedule slip and negligible change to the rest of the project objective would be categorized as "moderate." As with probability assessment, the more ranges there are, the better the characterization of risk, but the harder it is to achieve agreement among the project team.

Similar assessment may also be devised to look at specific kinds of risk separately, such as cost risk or schedule risk, to determine which risks are most likely to affect the highest project priorities.

The most precise assessment of impact defines specific estimates for each risk. Few risks relate only to a single aspect of the project, so this requires a collection of measurement estimates, including at least cost and schedule impact. Cost is conceptually the simplest, because it is unambiguously measured in dollars, yen, euros, or some other easily described unit, and any adverse variance will directly affect the project budget. Schedule impact is not as simple, for two reasons. The impact of a risk is generally in effort, and, as discussed in Chapters 4 and 5, the relation between effort and activity duration is not necessarily straightforward. In addition, not every duration increase for an activity necessarily represents an impact to the schedule. Activities not on a critical path (those with "float" or "slack") generate schedule impact only for adverse variances that are large enough to consume all available schedule flexibility. Estimating cost and schedule variances attributable to risks, as with other project estimating, is neither easy nor necessarily very accurate. Quantitative assessments of risk impact may look precise, but the quality of such estimates is highly variable.

There are other impacts of project risk that are even more difficult to measure. Some risks lead to required overtime or lower the morale of the project team. These represent real impacts on the current project, but they may be relatively small when measured only against the project objective. The longer-term impact, though, is significant if this is a chronic problem encountered frequently on an organization's projects. Mandatory overtime and low motivation are both root causes of turnover, so these impacts may lead to increased probability of other project risks, such as loss of key contributors. Another sort of impact is the effect on relationships with customers, suppliers, and others connected to the project. If a project problem "bruises" such a relationship, consequences in the long term can be quite significant. Increased stress and worry are consequences of risk on troubled projects, as are extra meetings (for global projects, extra meetings in the middle of the night, at least for some people). The impact of these factors on current and future projects may be very difficult to estimate. The correlation among schedule, cost, and other impacts for each risk is often complex. When something in a project is late, there are nearly always both out-of-pocket and other, more subtle costs involved.

Impact assessment on technical projects is not always confined strictly to project parameters. On some projects, concerns about health and safety are significant. Project work may involve poisonous or volatile chemicals, dangerous environments, or unusual modes of travel. While factors such as these are seldom a dominant source of risk impact, you should consider their potential effect on the people involved in your project.

Qualitative impact assessment using three to five categories is usually relatively easy, and it is sufficient for prioritizing risks on the basis of severity. Techniques such as polling, interviewing, team discussion, and reviews of planning data are effective for assigning risks to impact categories. As with probability assessment for each risk, the best foundation for quantitative estimates of impact is history, along with techniques such as Delphi, computer modeling, and consulting peers and experts.

For quantitative assessments of impact in situations that are common, statistics may be available. A good way to provide credible quantitative impact data is to select the mean of the distribution for initial estimates of duration or cost and use the difference between that estimate and the measured "90 percent" point. This principle is the basis for Program Evaluation and Review Technique (PERT) analysis. The PERT estimating technique was discussed in Chapter 4, and other aspects of PERT are covered later in this chapter and in Chapter 9.

Qualitative Risk Analysis

The minimum requirement for risk analysis is a sequenced list of risks, ordered by perceived severity. After assessing "loss" times "likelihood" for each risk, the highest one needs to be at the top of the list and the smallest one at the bottom. If the list of risks is short enough, you can order the list quickly on the basis of a few passes of pair-wise comparisons, switching any adjacent risks where the more severe of the two is lower on the list. The most serious exposures will bubble to the top, and the more trivial ones will sink to the bottom. This technique is best done by a single individual.

A similar technique, related to Delphi, combines data from lists sorted individually by each member of a team. The risks on each list are assigned a score equal to their position on the list, and all the scores for each risk are summed. The risk with the lowest total score heads the composite list, and the rest of the list is sorted by scores in increasing order. If there are significant variances in some of the lists (detected by "clumping" in the aggregated scoring data), further discussion and an additional iteration (as is done in Delphi estimating) may lead to better consensus. The resulting list is more objective than a sequence created by an individual, and it represents the thinking of the whole team.

While these sorting techniques result in an ordered risk list, such a list shows only relative risk severity, without indication of the project exposure that each risk represents.

Risk Assessment Tables

Qualitative risk assessment based on categorization of both probability and impact provides greater insight into the absolute risk severity. A risk assessment table or spreadsheet where risks are listed with category assignments for both probability and impact, as in Figure 7-1, is one approach for this.

Risks	Probability	Impact	Overall Risk

Figure 7-1: Risk assessment table.

After listing each risk, a category is assigned (such as High/ Moderate/Low) for both probability and impact. The last column, "Overall Risk," is filled in by combining the category information in the two columns or by assigning weights to the categories and using the product of the weights. Although any number of categories may be used, the quickest method that results in a meaningful sort uses three categories (defined as in the earlier discussions of probability and impact) and assigns either combinations of the categories or weights such as 1, 3, and 9 for low, moderate, and high, respectively. An example of a sorted qualitative assessment for five risks might look like Figure 7-2.

Risks	Probability (H/M/L)	Impact (H/M/L)	Overall Risk
Software Guru Is Not Available	M	H	HM
Consultant Is Incompetent	M	M	M
Purchased Component Comes Late	L	H	M
Software Development Is Too Slow	L	M	ML
Needed Test Gear Is Not Available	L	L	L

Figure 7-2: Risk assessment example.

For the data in the right column, categories may be combined (as shown), factors multiplied (the numbers would be 27, 9, 9, 3, and 1), or "stop light" icons displayed to indicate risk (with red for high, yellow for moderate, and green for low). From a table such as Figure 7-2, risks above a certain absolute assessment level, such as moderate, can be selected for risk management attention.

Risk Assessment Matrices

An alternative method for qualitative risk assessment involves placing risks on a two-dimensional matrix, where the rows and columns represent the categories of probability and impact. The matrices may be two-by-two, three-by-three, or larger. Risk matrices are generally square, but they may be rectangular with different numbers of categories for probability and impact. Figure 7-3 is an example of a five-by-five matrix.

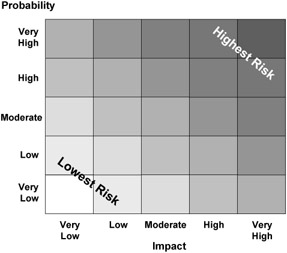
Figure 7-3: Risk assessment matrix.

The farther up and to the right a risk is assessed to be, the higher its overall assessment. Risks are selected for management on the basis of whether the cell in the matrix represents a risk above some predetermined level of severity.

Alternative Assumptions Testing

Standard project network charts do not permit the use of conditional branching, as system flowcharts and other graphical techniques do. Because it is not uncommon to have places in a project schedule where one of several possible alternatives, outcomes, or decisions will be chosen, you need some method for analyzing the situation. One qualitative way around this limitation is to construct a baseline plan using the assumption that seems most likely and deal with the other possible outcomes as risks. If it is not possible to determine which outcome may be most likely, it is usual to select the one that represents the longest duration (or highest cost) to use in the baseline plan. Assessing the risk associated with making an incorrect choice involves determining the probability that it may be wrong and any consequences (impact) on the project. To do this, you also must specifically identify any other potential outcomes, their probabilities, and the consequences to the project if each should occur instead of the outcome you assumed in your plan. Each of these other associated possible outcomes, with probability and impact assessments, then can be listed with project risks and assessed with them.

Data Precision Ranking

Not all risks are equally well understood. Some risks happen regularly, and experience and data concerning them are plentiful. Assessment of these risks, and formulation of adequate responses, is not difficult. Other risks in projects arise from the portions of the work that are new, unique, or different compared with work on other projects. Assessment of probability and impact for these risks may be based on imprecise or only partial information, so the assessment of risk may be too low.

Even with qualitative risk assessment, these poorly understood risks can be identified and singled out for special treatment. For each assessment, consider the quality, reliability, and integrity of the data used to categorize probability and impact. If the information seems inadequate, it may be prudent to seek out experts or other sources of better information or to err on the side of caution and adopt higher categories for probability and impact to ensure that the visibility of the risk is elevated and receives sufficient attention.

List of Risks that Require Further Attention

The main objective of qualitative risk assessment is to identify major risks by prioritizing the known project risks and rank-ordering them, with major risks at the head of the list and minor ones at the bottom. The sequenced list may be assembled using any of the methods described, but the use of three categories (low, moderate, and high) for both probability and impact generally provides a good balance of adequate analysis and minimal effort. However the list is analyzed and sorted, it needs to be partitioned into risks that deserve more consideration and risks that seem too minor to warrant a planned response.

The first several risks on your prioritized list nearly always require attention, but the question of how far down the list to go is not necessarily simple. One idea is to read down the list, focusing on the consequences and the likelihood of each risk until you reach the first one that will not keep you awake at night. The "gut feel" test is not a bad way to select the boundary for a sorted risk list. A similar idea uses consensus; team members individually select the cutoff point and then discuss as a team where the line should be, relying on individual and group experiences. It is also possible to set an absolute limit, such as moderate overall risk, or you can draw a diagonal stair-step boundary from the upper left to the lower right in a matrix. Whatever method you use, it is prudent to check each of the risks that are not selected to ensure that there are none that seem to need a response.

Following this examination, you are ready to prepare an abridged list of risks for potential further quantitative analysis and management.

Quantitative Risk Assessment

As stated earlier in the chapter, quantitative risk assessment involves more effort than qualitative techniques, so it is common to do initial sorting and selection of risks qualitatively. This is not absolutely necessary, though, because each of the qualitative methods discussed has a quantitative analogue that can be used to sequence the list. The tables and matrices have their categories for probability and impact replaced by absolute numerical estimates. Quantitative techniques such as sensitivity analysis, more rigorous statistical methods, decision trees, and simulations provide further insight into project risk, and can also be used for overall project risk assessment.

One other distinction between qualitative and quantitative assessment is that in quantitative risk assessment, the estimated impact for each identified risk is explicitly based only on consequences that affect the overall project. Sensitivity analysis, to determine the specific effect of each risk on the project, is an initial requirement for quantitative analysis of each activity risk.

Sensitivity Analysis

Not all risks are equally damaging. Schedule impact that arises from activity risks is significant only when the estimated slippage exceeds any available float. For simple projects, a quick inspection of the plan using the risk list will distinguish the risks that are likely to cause the most damage. For more complex networks of activities, using a copy of the project database that has been entered into a scheduling tool is a fast way to detect risks (and combinations of risks) that are most likely to result in project delay. If you make a copy of the project plan and replace the baseline estimates in the copy with longer estimates expected if there are problems, the computer will calculate and display overall project impact. By sequentially entering all the risk data and then backing it out, you can easily detect the quantitative schedule sensitivity for each risk.

In general, all adverse cost variances are summed to estimate budget overrun, but on some projects not all cost impact is accounted for in the same way. If a risk results in an out-of-pocket expense for the project, then it impacts the budget directly. If the cost impact involves a capital purchase, then the project impact may be only a portion of the actual cost, and in some cases the entire expense may be accounted for somewhere else. An increase in cost that is considered part of organizational overhead, such as allocation of a conference room to be used as a "war room" for the duration of a particularly troubled project, is seldom charged back to the project directly. Increased costs for communications, duplication, shipping, and other services considered routine are frequently not borne directly by technical projects. Travel costs in some cases may not be allocated directly to projects. While it is generally true that all cost and other resource impact is proportionate to the magnitude of the variance, it may be worthwhile to segregate potential direct cost variances from any that are indirect.

Quantitative Risk Assessment Tables

For quantitative assessment, the same sort of table or spreadsheet discussed previously can be filled in with numerical probabilities instead of with the categories used for qualitative assessment. As each risk is considered, its estimated impact in cost, effort, time (but only time in excess of any available scheduling flexibility), or other factors is used. Overall risk is then assessed as the product of the impact estimates and the selected probability. One drawback of using this method for sequencing risks is that for some risks it may be very time-consuming to develop consensus for both the impact and the probability. A second, more serious issue is that "impact" may be measured in more than one way (for example, in time and in money), making it difficult to ascertain a single uniform measure of overall risk.

While you could certainly list impacts of various kinds, weighted using the estimated probabilities, you may find that sorting on the basis of these data is not straightforward. This problem can be overcome by selecting one type of impact, such as time, and converting impact of other kinds into an equivalent project duration slip (as was done in the PERIL database). You could also develop several tables, one for cost, another for schedule, and others for scope, quality, safety, or any other type of impact for which you can develop meaningful numerical estimates. You can then sort each table on a consistent basis and select risks from each for further attention. This multiple-table process also requires you to do a final check to detect any risks that are significant only when all factors are considered together.

Two Dimensional Quantitative Analysis

The qualitative matrix converts to a quantitative tool by replacing the rows and columns with perpendicular axes. Probability may be plotted on the horizontal axis, from zero to 100 percent, and impact may be plotted on the vertical axis. Each risk identified represents a coordinate point in the two-dimensional space, and risks requiring further attention are found in the upper right, beyond a boundary defined as "risky." As with tables, this idea is most useful when all risks can be normalized to some meaningful single measure of impact, such as cost or time.

A variation on this concept plots risks on a pair of axes that represent estimated project cost and project schedule variances, representing each risk using a "bubble" that is sized proportionately with estimated probability instead of a single point. Since impact is higher for bubbles farther from the origin, several boundaries are defined for the graph. A diagonal close to the origin defines significant risk for the large (very likely) bubbles, and other diagonals farther out define significant exposure for the smaller bubbles. In Figure 7-4, there are several risks that are clearly significant. Risk F has the highest impact, and Risk E is, well, risky. Others would be selected on the basis of their positions relative to the boundaries of the graph.

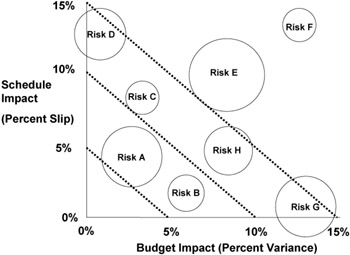
Figure 7-4: Risk assessment graph.

PERT

Program Evaluation and Review Technique (PERT) methodology, discussed briefly in Chapter 4, has assumed a number of meanings. The most common, which actually has little to do with PERT methodology, is associated with the graphical network of activities used for project planning, often referred to as a "PERT chart." Similar networks are used for traditional PERT analysis, but PERT methodology goes beyond the deterministic point estimates of duration to which so-called PERT charts are generally limited. A second, slightly less common meaning for PERT relates to estimating, which is discussed in the context of schedule risk in Chapter 4. The original purpose of PERT was actually much broader than this.

PERT for Quantitative Activity Risk Analysis

The principal reason PERT was developed in the late 1950s was to help the U.S. military manage risk on large defense projects. PERT was used on the development of the Polaris missile systems, on the NASA manned space projects, including the Apollo moon missions, and on countless other government projects. The motivation behind all of this was the observation that the larger the program became, the more delayed it seemed to be and the higher the cost overruns became. PERT was developed to provide a better basis for setting expectations on these massive, expensive endeavors.

PERT is a specific example of quantitative risk analysis, and it is applied to both schedule (PERT Time) and budget (PERT Cost) exposures. PERT is based on statistical analysis of the project plan, using both estimates of likely outcomes and estimates of the uncertainty for these outcomes. PERT techniques may be used to analyze all project activities or only those activities that represent high perceived risk. In either case, PERT also provides data on overall project risk. This application of PERT methodology is covered in Chapter 9.

PERT Time was mentioned in Chapter 4, using three estimates for each activity—an optimistic estimate, a most likely estimate, and a pessimistic estimate—to calculate an "expected estimate." PERT Cost also uses three estimates to derive an expected activity cost, using essentially the same formula:

ce = (co + 4cm + cp)/6, where

ce is the "expected" cost

co is the "optimistic" (lowest realistic) cost

cm is the "most likely" cost

cp is the "pessimistic" (highest realistic) cost

As with PERT Time, the standard deviation is estimated to be (cp - co)/6. A distribution showing this graphically is in Figure 7-5.

Figure 7-5: Cost estimates for PERT analysis.

PERT Cost estimates are generally done in monetary units (e.g., pesos, rupees, euros), but they may also be evaluated in effort (person-hours, engineer-days) instead of, or in addition to, the financial estimates.

The earlier discussion of estimating focused on developing credible duration estimates, using pessimistic (or worst-case) estimates to adjust the baseline estimates used for planning. Whether or not the estimates in a preliminary project plan are derived this way, PERT analysis of activity-associated risks is an effective way to assess both cost and schedule impact.

Probability Density Functions

Risk impact discussed so far in this chapter has been based on single-point, deterministic estimates. PERT assumes a continuum of possibilities, defined by a statistical distribution (or, less commonly, by discrete data values that define a histogram). The commonly used formulas assume a Beta distribution, a bell-shaped probability density function that may be symmetric (equivalent to the Normal distribution) or one skewed to the right or left, depending on its parameters. Figure 7-5 is an example of a Beta distribution for activity cost. The formulas also assume that the optimistic and pessimistic estimates bound nearly all the possibilities, with about 98 percent (or in other variants 90 or 80 percent) of the distribution inside the range bounded by the optimistic and pessimistic estimates.

Other distributions may also be used for modeling potential outcomes. These include:

• Triangular (a linear rise from optimistic estimate to the most likely, followed by a linear decline to the pessimistic estimate, Figure 7-7)
• Normal (the Gaussian bell-shaped curve, with the most likely and expected values halfway between the extremes, Figure 7-8)
• Uniform (all values in the range are assumed equally likely, also with the most likely and expected values both at the midpoint, Figure 7-9)

There are also more exotic distributions.

Although dozens of statistical distributions and limitless histograms are possible, the precise shape of the distribution turns out to be relatively unimportant, because the shape of the distribution has only a minor effect on the two parameters that matter the most in risk analysis: the mean and the standard deviation of the distribution. Assessment of risk in PERT relies only on these two parameters, which tend to be roughly equivalent regardless of the distribution you chose. In addition, although it is theoretically possible to carry out a PERT analysis mathematically, it is impractical. PERT analysis is nearly always done by computer simulation (based on pseudorandom number generation and algorithms that approximate the chosen distributions) or by rough manual methods that estimate the results. The choice of a distribution type for each activity has little effect on quantitative assessment of risk for most projects.

For those who may be interested, some examples follow that show why the choice of a probability density function for the estimates is not terribly crucial. If you do not need convincing of this, just note that any approach that you find easy to work with can produce useful quantitative risk data, and skip ahead to the discussion of setting the estimate ranges for PERT.

PERT has generally assumed that the three estimates used are all located along a continuum. The shape of the distribution that these estimates define does not have a substantial effect on the resulting analysis, even if only two estimates are used, one "most likely" and a second "worst-case." These set the range and are sufficient to provide useful estimates of risk. Between the two limits, on the basis of the expected time (or cost) variance, PERT formulas generate results for risk assessment.

For Figure 7-6, the optimistic estimate is assumed identical to the most likely. If the plan estimates the activity duration as te, the calculated expected duration, schedule risk impact (assuming this activity is schedule-critical) is most of the difference between te and tp.

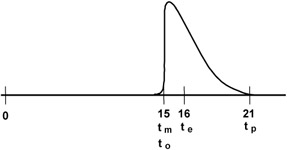
Figure 7-6: Two-estimate PERT Beta distribution.

When values are plugged into the formula to calculate the expected duration—for example, using fifteen days for to and tm and twenty-one days for tp—the PERT formula results in a te of sixteen days.

A similar result, mathematically much simpler, could be estimated using a triangular distribution, as in Figure 7-7.

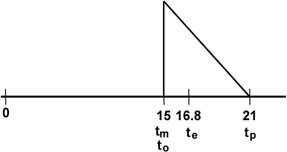
Figure 7-7: Triangular distribution.

For a triangular distribution, the point at which the areas to the right and left are equal occurs slightly less than 30 percent of the way along the triangle's base. (It is 1 minus the square root of .5, or .292893, which is many more digits of accuracy than this analysis warrants. Even .3 is greater precision than necessary.) Using the same estimates as before for to, tm, and tp, the estimate for te is just under 16.8 days.

Symmetric distributions increase the expected estimate a little more. Using a Normal distribution (Figure 7-8) or a simple Uniform distribution (Figure 7-9) for the probability distribution that lies between the range limits results in an expected value for this example of eighteen days.

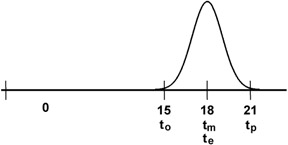
Figure 7-8: Normal distribution.

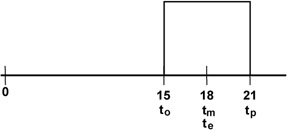
Figure 7-9: Uniform distribution.

The PERT formula for the Beta distribution in Figure 7-5 estimates sixteen days, and all the other examples are a bit higher. For a quantitative risk assessment, some value above the mean is selected to represent impact (the "90 percent" point is common). Although these points are also not identical for the various distributions, they all are quite close together, near the upper (tp) estimate. Risk assessment is related to the variance for the chosen distribution, which for these examples will all be similar because, in each case, the range is the same.

If tp is twenty-one days, the "90 percent" point for all of these distributions is about twenty days (rounded off to the nearest whole day). Whichever distribution might be selected, there is only a "moderate" risk (roughly 10 percent of the time) that the sixteen-day expected duration will be four or more days late. There are many PERT tools and techniques capable of calculating all of this with very high precision, displaying many (seemingly) significant digits in the results. Considering the precision and expected accuracy of the input data, though, the results are at best accurate only to the nearest whole day. Arguing over the "best" distribution to use and endlessly fretting over how to proceed are not a good investment of your time. Almost any reasonable choice of distribution will result in comparable and useful results for risk analysis, so use the choice that is easiest for you to implement.

At the project level, where PERT data for all the activities is combined, the distributions chosen for each activity become even more irrelevant. The larger the project, the more the overall analysis for project cost and duration tends to approximate a Normal bell-shaped curve (more on this in Chapter 9).

Setting Ranges for PERT

What does matter a great deal for risk assessment is the range specified for the estimates. Setting the range to be too narrow (which is a common bias) materially diminishes the quantitative perception of risk. Risk, assessed using PERT analysis, is based on the total expected variation in possible outcomes, and this varies directly with the size of the estimate range.

Arriving at credible upper and lower limits for cost and duration estimates is usually the most difficult aspect of PERT. One way to develop these data is through further analysis of potential root causes for each activity that has substantial perceived risk. As is discussed in Chapter 4, the most powerful tool for estimating the upper limit of an activity duration is to seek worst-case scenarios and be as realistic as possible concerning the consequences of potential problems. It is easy to minimize or overlook the potential impact of risk scenarios, particularly when planning is not thorough.

When there is sufficient historical information available, the limits (and possibly even the shape) of the distribution may be inferred from the data population. Discussions and interviews with experts, project stakeholders, and contributors may also provide information that will be useful in setting credible range boundaries.

In any event, one quantitative assessment of risk impact for each activity is determined using the difference between the expected and the pessimistic (or worst-case) PERT estimates. There is more about using PERT methodology for project-level risk assessment in Chapter 9.

Decision Trees

Decision trees may also be used to assess risks when only a small number of options or potential outcomes are possible. Decision analysis for risks is a quantitative version of the project assumption testing (discussed earlier with other qualitative assessment techniques). Decision trees are generally used to evaluate several options prior to selecting one of them to execute. The concept is applied to risk analysis in a project by using the weights and estimates to ascertain potential impact for specific alternatives.

Whenever there are points in the project where several options are possible, each can be planned and assigned a probability (the sum for all options totaling 100 percent). As with PERT, an "expected" estimate for either duration or cost may be derived by weighting the estimates for each option and summing these figures to get a "blended" result. Using the data in Figure 7-10, a project plan containing a generic activity (that could be any of the three options) with an estimate of sixteen days would result in a more realistic plan than simply using the twelve-day estimate in the "most likely" option. The schedule exposure of the risk situation here may be estimated by noting the maximum adverse variance (an additional four days, if the activity is schedule-critical) and associating this with an expected probability of 35 percent.

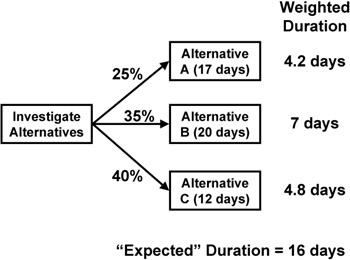
Figure 7-10: Decision tree for duration.

Decision analysis may also be used to guide project choices based on costs. It provides information on the options that offer the lowest expected cost, as well as the lowest expected cost variance. Whenever there are several ways to proceed in a project—for example, by either upgrading existing equipment or purchasing new hardware—decision analysis can be effective in determining the choice that minimizes project risks. The analysis of costs in Figure 7-11 argues for replacement to minimize cost variance (none, instead of the $20,000 to $120,000 associated with upgrade) and for upgrade to minimize the expected cost. As is usual on projects, there is a trade-off between minimizing project parameters and minimizing risk—you must decide which is more important and balance the decisions with your eyes open.

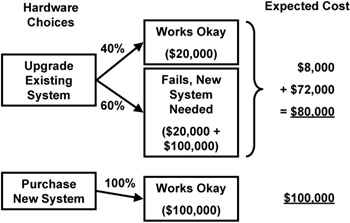
Figure 7-11: Decision tree for cost.

Simulation and Modeling

Decision trees are useful for situations where you have discrete estimates. In more complex cases, options may be modeled or simulated using Monte Carlo or other computer techniques. If the range of possibilities for an activity's duration or cost is assumed to be a statistical distribution, the standard deviation (or variance) of the distribution is a measure of risk. The larger the range selected for the distribution, the higher the risk for that activity. For single activities, modeling with a computer is rarely necessary, but when several activities (or the project as a whole) are considered together, computer-based simulations are useful and effective. Both software tools and manual approximations for this are key topics in Chapter 9.

Key Ideas for Activity Risk Analysis

• Assess probability and impact for each project risk.
• Use qualitative risk analysis to prioritize risks.
• Apply quantitative risk analysis techniques to significant risks.
• If you use PERT, keep it simple.

Panama Canal Risks (1906 1914)

As with any project of the canal's size and duration, risks were everywhere. On the basis of assessment of cost and probability, the most severe were diseases, mud slides, the constant use of explosives, and the technical challenges of constructing the locks.

Diseases were less of a problem on the U.S. project, but health remained a concern. Both of the first two managers cited tropical disease among their reasons for resigning from the project. Life in the tropics in the early 1900s was neither comfortable nor safe. The enormous death toll from the earlier project made this exposure a top priority.

Mud slides were common during both the French and the U.S. projects, as the soil of Panama is not stable, and earthquakes made things worse. Whenever the sloping sides of the cut collapsed, there was danger to the working crews and potential serious damage to the digging and railroad equipment. In addition to this, it was demoralizing to face the repair and rework following each slide, and the predicted additional effort required to excavate repeatedly in the same location multiplied the cost of construction. This risk had very high impact to both schedule and budget; despite precautions, major setbacks were frequent.

Explosives were in use everywhere. In the Culebra Cut, massive boulders were common, and workers set off dynamite charges to reduce them to movable pieces. The planned transit for ships through the manmade lakes was a rain forest filled with large, old trees, and these, too, had to be removed with explosives. In the tropics especially, the dynamite of that era was not very stable. It exploded in storage, in transit to the work sites, while being set in place for use, and in many other unintended situations. The probability of premature detonation was high, and the risk to human life was extreme.

Beyond these daunting risks, the largest technical challenge on the project was the locks. They were gigantic mechanisms, among the largest and most complex construction ever attempted. Although locks had been used on canals for a very long time, virtually all of them had been built for smaller boats navigating freshwater rivers and lakes. Locks had never before been constructed for large ocean-going ships. (The canal at Suez has no locks; as with the original plan for Panama, it is entirely at sea level.) The doors for the locks were to be huge and, therefore, very heavy. The volume of water held by the locks when filled was so great that the pressure on the doors would be immense, and the precision required for the seams where the doors closed to hold in the water was also unprecedented for manmade objects so large. The locks would be enormous boxes with sides and bottoms formed of concrete, which also was a challenge, particularly in an earthquake zone. For all this, the biggest technological hurdle was the requirement that all operations be electric. Because earlier canals were much smaller, usually the lock doors were cranked open and shut and the boats were pulled in and out by animals. (To this day, the trains used to guide ships into and out of the locks at Panama are called "electric mules.") The design, implementation, and control of a canal using the new technology of electric power—and the hydroelectric installations required to supply enough electricity—all involved emerging, poorly understood technology. Without the locks, the canal would be useless, and the risks associated with resolving all of these technical problems were large.

These severe risks were but a few of the many challenges planners faced on the canal project, but each was singled out for substantial continuing attention. Their responses are summarized at the end of the next chapter, in which tactics for dealing with risk are covered.