Power Computation Details

---

This section provides information on how the power is computed in the Analyst Application. When you request that sample size be computed, the computations produce the smallest sample size that provides the specified power.

Hypothesis Tests

The power for the one-sample t-test, the paired t-test, and the two-sample t-test is computed in the usual fashion. That is, power is the probability of correctly rejecting the null hypothesis when the alternative is true. The sample size is the number per group; these calculations assume equally sized groups. To compute the power of a t-test, you make use of the noncentral t distribution. The formula (O'Brien and Lohr 1984) is given by

• Power = Prob(t > t_crit, v, NC)

for a one-sided alternative hypothesis and

• Power = Prob(t > t_critu, v, NC) + Prob(t < t_critl, v, NC)

for a two-sided alternative hypothesis where t is distributed as noncentral t(NC, v).

t_crit = t_(1-α,v) is the (1 - α) quantile of the t distribution with v df

t_critu = t_(1-α/2,v) is the (1-α/2) quantile of the t distribution with v df

t_critl = t_(α/2,v) is the (α/2) quantile of the t distribution with v df

For one sample and paired samples,

v = n - 1	is the df
NC =	is the noncentrality parameter

For two samples,

v = 2(n - 1)	is the df
NC =	is the noncentrality parameter

Note that n equals the sample size (number per group). The other parameters are

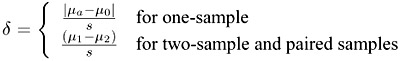
One-Way ANOVA

The power for the one-way ANOVA is computed in a similar manner as for the hypothesis tests. That is, power is the probability of correctly rejecting the null (all group means are equal) in favor of the alternative hypothesis (at least one group mean is not equal), when the alternative is true. The sample size is the number per group; these calculations assume equally sized groups. To compute the power, you make use of the noncentral F distribution. The formula (O'Brien and Lohr 1984) is given by

• Power = Prob(F > F_crit, v₁, v₂, NC)

where F is distributed as the noncentral F(NC, v₁, v₂) and F_crit = is the (1 - α) quantile of the F distribution with v₁ and v₂ degrees of freedom.

v1 = r - 1	is the numerator df
v2 = r(n - 1)	is the denominator df
n	is the number per group
r	is the number of groups
NC =	is the noncentrality parameter
CSS = (μg - μ.)2 is the corrected sum of squares
μg	is the mean of the gth group
μ.	is the overall mean
σ2	is estimated by the mean squared error (MSE)

Confidence Intervals

Power calculations are available when the proposed analysis is construction of confidence intervals of a mean (one-sample) or difference of two means (two-samples or paired-samples). To understand the power of a confidence interval, first define the precision to be half the length of a two-sided confidence interval (or the distance between the endpoint and the parameter estimate in a one-sided interval). The power can then be considered to be the probability that the desired precision is achieved, that is, the probability that the length of the two-sided interval is no more than twice the desired precision. Here, a slight modification of this concept is used. The power is considered to be the conditional probability that the desired precision is achieved, given that the interval includes the true value of the parameter of interest. The reason for the modification is that there is no reason to want the interval to be particularly small if it does not contain the true value of the parameter.

To compute the power of a confidence interval or an equivalence test, you make use of Owen's Q formula (Owen 1965). The formula is given by

where

and

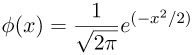
The power of a confidence interval (Beal 1989) is given by

where

tc =	is the (1 - αs/2) quantile of a t distribution with v df
α	is the confidence level

Equivalence Tests

In a test of equivalence, a treatment mean and a reference mean are compared to each other. Equivalence is taken to be the alternative hypothesis, and the null hypothesis is nonequivalence. The power of a test is the probability of rejecting the null hypothesis when the alternative is true, so in this case, the power is the probability of failing to reject equivalence when the treatments are in fact equivalent, that is, the treatment difference or ratio is within the prespecified boundaries.

The computational details for the power of an equivalence test (refer to Phillips 1990 for the additive model; Diletti, Hauschke, and Steinijans 1991 for the multiplicative) are as follows:

• Power = Prob(t₁ ≥ t_{(1 - α,v)} and t₂ ≤ - t_{(1 - α,v)}|bioequivalence)

Owen (1965) showed that (t₁, t₂) has a bivariate noncentral t distribution that can be calculated as the difference of two definite integrals (Owen's Q function):

• Power = Q_v(-t_(1-α,v),δ₂; 0, R) - Q_v(t_(1-α,v), δ₁; 0, R)

where t_(1-α,v) is the (1 - α) quantile of a t distribution with v df.

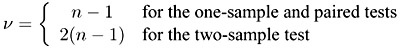
and

V	is the coefficient of variation
bl	is the lower equivalence bound
bu	is the upper equivalence bound

For equivalence tests, alpha is usually set to 0.05, and power ranges from 0.70 to 0.90 (often set to 0.80).

For the additive model of equivalence, the values you must enter for the null difference, the coefficient of variation (c.v.), and the lower and upper bioequivalence limits must be expressed as percentages of the reference mean. More information on specifications follow:

• Calculate the null difference as , where μ_T is the hypothesized treatment mean and μ_R is the hypothesized reference mean. The null difference is often in the range of 0 to 0.20.

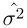• For the coefficient of variation value, σ can be estimated by , where is the residual variance of the observations (MSE). Enter the c.v. as a percentage of the reference mean, so for the c.v., ente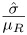r , or 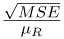. This value is often in the range of 0.05 to 0.30.

• Enter the bioequivalence lower and upper limits as percentages of the reference mean as well. That is, for the bounds, enter and 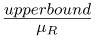. These values are often -0.2 and 0.2, respectively.

For the multiplicative model of equivalence, calculate the null ratio as , where μ_T is the hypothesized treatment mean and μ_R is the hypothesized reference mean. This value is often in the range of 0.80 to 1.20. More information on specifications follow:

• The coefficient of variation (c.v.) is defined as 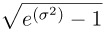. You can estimate σ by 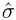, where 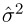is the residual variance of the logarithmically transformed observations. That is, σ can be estimated by 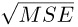from the ANOVA of the transformed observations. The c.v. value is often in the range of 0.05 to 0.30.

• The bioequivalence lower and upper limits are often set to 0.80 and 1.25, respectively.

---