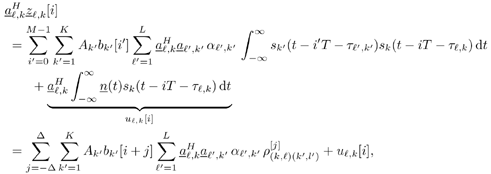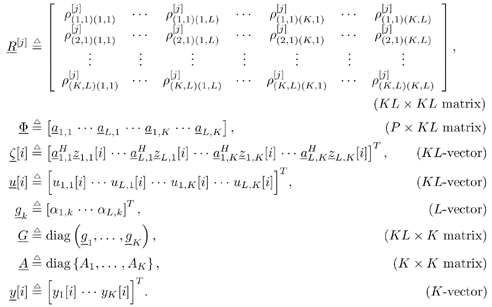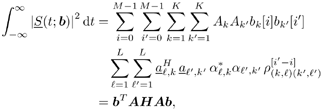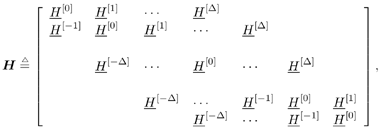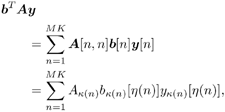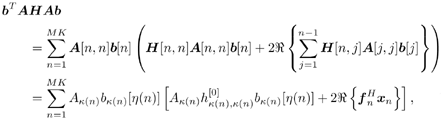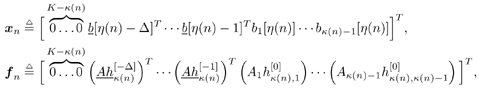5.3 Optimal Space-Time Multiuser Detection
| In Section 5.2, we considered (linear) spatial processing as a mechanism for separating multiple users sharing identical temporal signatures. In the remainder of this chapter we examine the situation in which both temporal and spatial signatures of the users differ and consider the joint exploitation of these differences to separate users. Such joint processing is known as space-time processing . In this and the following sections, we discuss such processing in the context of multiuser detection in a CDMA system with multipath channel distortion and multiple receive antennas. We begin in this section with consideration of optimal (nonlinear) processing, turning in subsequent sections to linear and adaptive linear methods . The materials in this and the next sections first appeared in [554]. 5.3.1 Signal ModelConsider a DS-CDMA mobile radio network with K users, employing normalized spreading waveforms s 1 , s 2 , . . . s K , and transmitting sequences of BPSK symbols through their respective multipath channels. The transmitted baseband signal due to the k th user is given by Equation 5.42 where M is the number of data symbols per user per frame, T is the symbol interval, b k [ i ] Equation 5.43 where N is the processing gain, { c j,k : j = 0, . . ., N “ 1} is a signature sequence of ±1's assigned to the k th user, and y is a normalized chip waveform of duration T c = T/N. At the receiver an antenna array of P elements is employed. Assuming that each transmitter is equipped with a single antenna, the baseband multipath channel between the k th user's transmitter and the base station receiver can be modeled as a single-input/multiple-output channel with the following vector impulse response: Equation 5.44 where L is the number of paths in each user's channel, a Equation 5.45 where * denotes convolution; n (t) = [ n 1 ( t ) · · · n P ( t )] T is a vector of independent zero-mean complex white Gaussian noise processes, each with power spectral density s 2 . 5.3.2 Sufficient StatisticWe next derive a sufficient statistic for demodulating the multiuser symbols from the space-time signal model (5.45). To do so, we first denote the useful signal in (5.45) by Equation 5.46 where Equation 5.47 where Equation 5.48 The first integral in (5.48) can be expressed as Equation 5.49 Since the second integral in (5.48) does not depend on the received signal r ( t ), by (5.49) we see that { y k [ i ]} is a sufficient statistic for detecting the multiuser symbols b . From (5.49) it is seen that this sufficient statistic is obtained by passing the received signal vector r ( t ) through KL beamformers directed at each path of each user's signal, followed by a bank of K maximum-ratio multipath combiners (i.e., RAKE receivers). Since this beamformer is a spatial matched filter for the array antenna receiver, and a RAKE receiver is a temporal matched filter for multipath channels, the sufficient statistic { y k [ i ]} i;k is simply the output of a space-time matched filter . Next we derive an explicit expression for this sufficient statistic in terms of the multiuser channel parameters and transmitted symbols, which is instrumental to developing various space-time multiuser receivers in subsequent sections. Assume that the multipath delay spread of any user signal is limited to at most D symbol intervals, where D is a positive integer. That is, Equation 5.50 Define the following cross- correlations of the delayed user signaling waveforms: Equation 5.51 Since t l,k Equation 5.52 where { u l,k [ i ]} are zero-mean complex Gaussian random sequences with the following covariance: Equation 5.53 where I p denotes a p x p identity matrix and d ( t ) is the Dirac delta function. Define the following quantities : We can then write (5.52) in the following vector form: Equation 5.54 where ° denotes the Schur matrix product (i.e., elementwise product), and from (5.53) the covariance matrix of the complex Gaussian vector sequence { u [ i ]} is Equation 5.55 Substituting (5.54) into (5.49), we obtain a useful expression for the sufficient statistic y [ i ], given by Equation 5.56 where { v [ i ]} is a sequence of zero-mean complex Gaussian vectors with covariance matrix Equation 5.57 Note that by definition (5.51) we have 5.3.3 Maximum-Likelihood Multiuser Sequence DetectorWe now use the sufficient statistic above to derive the maximum-likelihood detector for symbols in b . The maximum-likelihood sequence decision rule chooses b that maximizes the log-likelihood function (5.48). Using (5.46), the second integral in (5.48) can be computed as Equation 5.58 where H denotes the following MK x MK block Jacobi matrix: Equation 5.59 Substituting (5.49) and (5.58) into (5.48), the log-likelihood function W ( b ) can then be written as Equation 5.60 For any integer n satisfying 1
Equation 5.61 Equation 5.62 where in (5.62) the vectors x n and f n have dimensions D K + K “1, given, respectively, by where Equation 5.63 where Equation 5.64 with the state vector recursively defined according to x n +1 = [ x n [2], . . . , x n [ D K + K “ 1], x n ] T and x 1 = ( D K + K “1), where m denotes a zero vector of dimension m . Given the additive decomposition (5.63) of the log-likelihood function, it is straightforward to apply the dynamic programming to compute the sequence |
EAN: 2147483647
Pages: 91
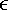 {+1, “1} is the
{+1, “1} is the 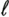 ,k
,k 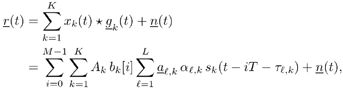
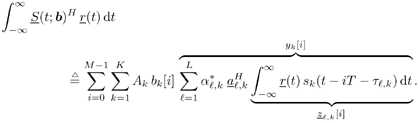
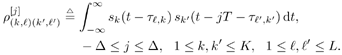
 D
D