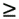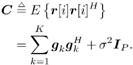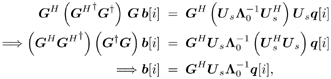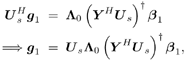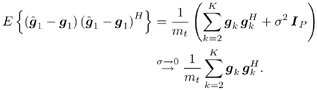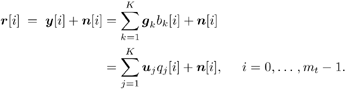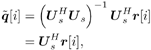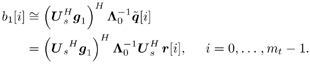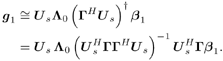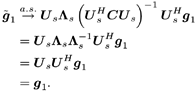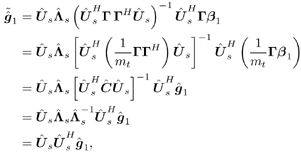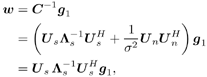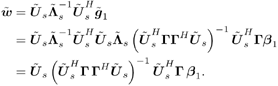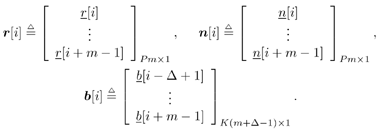5.2 Adaptive Array Processing in TDMA Systems
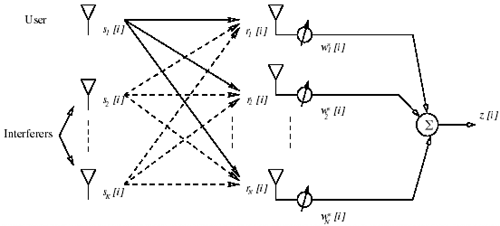
5.2.1 Signal ModelA wireless cellular communication system employing adaptive antenna arrays at the base station is shown in Fig. 5.1, where a base with P antenna elements receives signals from K users. The K users operate in the same bandwidth at the same time. One of the signals is destined to the base. The other signals are destined to other bases, and they interfere with the desired signal; that is, they constitute co-channel interference. Note that although here we consider the uplink scenario (mobile to base), where antenna arrays are most likely to be employed, the adaptive array techniques discussed in this section apply to the downlink (base to mobile) as well, provided that a mobile receiver is equipped with multiple antennas. The general structure can be applied to other systems as well. Figure 5.1. Wireless communication system employing adaptive arrays at the base station. An array of P antenna elements at the base receives signals from K co-channel users, one of which is the desired user 's signal, and the rest are interfering signals. The received signal at the antenna array is the superposition of K co-channel signals from the desired user and the interferers, plus the ambient channel noise. Assume that the signal bandwidth of the desired user and the interferers is smaller than the channel coherence bandwidth, so that the signals are subject to flat fading. Assume also that the fading is slow, such that the channel remains constant during one time slot containing M data symbol intervals. To focus on the spatial processing, we assume for the time being that all users employ the same modulation waveform, [1] so that after matched filtering with this waveform, the P -vector of received complex signal at the antenna array during the i th symbol interval within a time slot can be expressed as
Equation 5.1 where b k [ i ] is the i th symbol transmitted by the k th user, g k = [ g 1, k · · · g P,k ] T is a complex vector (the steering vector) representing the response of the channel and array to the k th user's signal, and n [ i ] ~ N c ( , s 2 I P ) is a vector of complex Gaussian noise samples. It is assumed that all users employ phase-shift-keying (PSK) modulation with all symbol values being equiprobable. Thus, we have The n th element of the steering vector g k can be expressed as Equation 5.2 where A k is the transmitted complex amplitude of the k th user's signal, g n,k is the complex fading gain between the k th user's transmitter and the n th antenna at the receiver, and a n,k is the response of the n th antenna to the k th user's signal. It is also assumed that the data symbols of all users { b k [ i ]} are mutually independent and that they are independent of the ambient noise n [ i ]. The noise vectors { n [ i ]} are assumed to be i.i.d. with independent real and imaginary components . Note that, mathematically, the model (5.1) is identical to the synchronous CDMA model of (2.1). However, the different physical interpretation of the various quantities in (5.1) leads to somewhat different algorithms than those discussed previously. Nevertheless, this mathematical equivalence will be exploited in the sequel. 5.2.2 Linear MMSE Combining Throughout this section we assume that user 1 is the desired user. In adaptive array processing, the received signal r [ i ] is combined linearly through a complex weight vector w In linear MMSE combining [570], the weight vector w is chosen such that the mean-square error between the transmitted symbol b 1 [ i ] and the array output z [ i ] is minimized: Equation 5.3 where the expectation is taken with respect to the symbols of interfering users { b k [ i ] : k In practice, the autocorrelation matrix C and the steering vector of the desired user g 1 are not known a priori to the receiver, and therefore they must be estimated in order to compute the optimal combining weight w in (5.3). In several TDMA-based wireless communication systems (e.g., GSM, IS-54 and IS-136), the information symbols in each slot are preceded by a preamble of known synchronization symbols, which can be used for training the optimal weight vector. The trained weight vector is then used for combining during the demodulation of the information symbols in the same slot. Assume that in each time slot there are m t training symbols and M “ m t information symbols. Two popular methods for training the combining weights are the least-mean-squares (LMS) algorithm and the direct matrix inversion (DMI) algorithm [570]. The LMS training algorithm is as follows . Algorithm 5.1: [LMS adaptive array]
Although the LMS algorithm has a very low computational complexity, it also has a slow convergence rate. Given that the number of training symbols in each time slot is usually small, it is unlikely that the LMS algorithm will converge to the optimum weight vector within the training period. The DMI algorithm for training the optimum weight vector essentially forms the sample estimates of the autocorrelation matrix C and the steering vector g 1 using the signal received during the training period and the known training symbols, and then computes the combining weight vector according to (5.3) using these estimates. Specifically, it proceeds as follows. Algorithm 5.2: [DMI adaptive array]
It is easily seen that the sample estimates 5.2.3 Subspace-Based Training Algorithm Notice that the sample correlation matrix Equation 5.9 However, the sample estimate Steering Vector Estimation In what follows it is assumed that the number of antennas is greater than the number of interferers (i.e., P Equation 5.10 The eigendecomposition of C is given by Equation 5.11 where as in previous chapters, U = [ U s U n ], L = diag { L s , s 2 I P “K }; L s = diag { l 1 , . . . , l K } contains the K largest eigenvalues of C in descending order, and U s = [ u 1 · · · u K ] contains the corresponding orthogonal eigenvectors; and U n = [ u K +1 · · · u P ] contains the ( N “ K ) orthogonal eigenvectors that correspond to the smallest eigenvalue s 2 . Denote Proposition 5.1: Given the eigendecomposition (5.11) of the autocorrelation matrix C , suppose that a received noise-free signal is given by Equation 5.12 Then the k th user's transmitted symbol can be expressed as Equation 5.13 Proof: Denote Equation 5.14 Denote further Equation 5.15 Then from (5.10) and (5.11) we have Equation 5.16 Taking the Moore “Penrose generalized matrix inverse [189] on both sides of (5.16), we obtain Equation 5.17 From (5.14) and (5.17) we then have Equation 5.18 where the last equality follows from the fact that Suppose now that the signal subspace parameters U s , L s , and s 2 are known. We next consider the problem of estimating the steering vector g 1 of the desired user, given m t training symbols { b 1 [ i ], i = 0, . . . , m t “ 1}, where m t Proposition 5.2: Let Equation 5.19 where U s and L are defined in (5.11) and (5.15), respectively. Proof: The i th received noise-free array output vector can be expressed as Equation 5.20 Denote Equation 5.21 since Equation 5.22 Equation 5.23 Equation (5.23) can be written in matrix form as Equation 5.24 Since rank ( Y ) = K and rank ( U s ) = K , we have rank ( Y H U s ) = K . Therefore, g 1 can be obtained uniquely from (5.24) by where the last equality follows from the fact that We can interpret the result above as follows. If the length of the data frame tends to infinity (i.e., M In practice, the received signals are corrupted by ambient noise: Equation 5.25 Since n [ i ] ~ N c ( , s 2 I P ), the log- likelihood function of the received signal r [ i ] conditioned on q [ i ], is given by Hence the maximum-likelihood estimate of q [ i ] from r [ i ] is given by Equation 5.26 where the last equality follows from the fact that Equation 5.27 Denote Equation 5.28 Solving g 1 from (5.28), we obtain Equation 5.29 To implement an estimator of g 1 based on (5.29), we first compute the sample autocorrelation matrix Equation 5.30 The steering vector estimator for the desired user is then given by Equation 5.31 Note that Interestingly, if on the other hand, we replace Proposition 5.3: Let the eigendecomposition of the sample autocorrelation matrix Equation 5.32 If we form the following estimator for the steering vector p 1 , Equation 5.33 then Equation 5.34 Proof: Using (5.33), we have where in the third equality we have used (5.6) and (5.7), and where the fourth equality follows from (5.32). Therefore, in the absence of noise, Weight Vector CalculationThe linear MMSE array combining weight vector in (5.3) can be expressed in terms of the signal subspace components, as stated by the following result. Proposition 5.4: Let U s and L s be the signal subspace parameters defined in (5.11); then the linear MMSE combining weight vector for the desired user 1 is given by Equation 5.35 Proof: The linear MMSE weight vector is given in (5.3). Substituting (5.11) into (5.3), we have where the last equality follows from the fact that the steering vector is orthogonal to the noise subspace (i.e., By replacing U s , L s , and g 1 in (5.35) by the corresponding estimates [i.e., Equation 5.36 Finally, we summarize the subspace-based adaptive array algorithm discussed in this section as follows. Algorithm 5.3: [Subspace-based adaptive array for TDMA] Denote
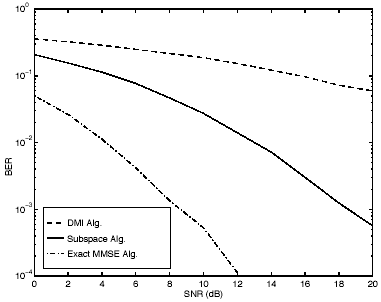
5.2.4 Extension to Dispersive ChannelsSo far we have assumed that the channels are nondispersive [i.e., there is no intersymbol interference (ISI)]. We next extend the techniques considered in previous subsections to dispersive channels and develop space-time processing techniques for suppressing both co-channel interference and intersymbol interference. Let D be the delay spread of the channel (in units of symbol intervals). Then the received signal at the antenna array during the i th symbol interval can be expressed as Equation 5.40 where g l,k is the array steering vector for the k th user's l th symbol delay and Then from (5.40) we can write Equation 5.41 where P is a matrix of the form with Here, as before, m is the smoothing factor and is chosen such that the matrix G is a "tall" matrix [i.e., Pm with To apply the subspace-based adaptive array algorithm, we first estimate the signal subspace ( U s , L s ) of C by forming the sample autocorrelation matrix of r [ i ] and then performing an eigendecomposition. Notice that the rank of the signal subspace is K x ( m + D “ 1). Once the signal subspace is estimated, it is straightforward to apply the algorithms listed in Section 5.2.3 to estimate the data symbols. Simulation Examples In what follows we provide some simulation examples to demonstrate the performance of the subspace-based adaptive array algorithm discussed above. In the following simulations, it is assumed that an array of P = 10 antenna elements is employed at the base station. The number of symbols in each time slot is M = 162 with m t = 14 training symbols, as in IS-54/136 systems. The modulation scheme is binary PSK (BPSK). The channel is subject to Rayleigh fading, so that the steering vectors { g k , k = 1, . . . , K } are i.i.d. complex Gaussian vectors, In the first example we compare the performance of the two steering vector estimators Figure 5.2. Comparison of normalized root MSEs of the subspace steering vector estimator and sample correlation steering vector estimator. In the next example we compare the BER performance of the subspace training method and that of the DMI training method. The simulated system is the same as in the previous example. The BER curves of the three array combining methods, namely, the exact MMSE combining (5.3), the subspace algorithm, and the DMI method (5.6) “(5.8), are plotted in Fig. 5.3. It is evident from this figure that the subspace training method offers substantial performance gain over the DMI method. Figure 5.3. BER performance of the subspace training algorithm, DMI algorithm, and exact MMSE algorithm in a nondispersive channel. Finally, we illustrate the performance of the subspace-based spatial-temporal technique for jointly suppressing co-channel interference (CCI) and intersymbol interference (ISI). The simulated system is the same as above, except now the channel is dispersive with D = 1. It is assumed that Figure 5.4. BER performance of the subspace training algorithm, DMI algorithm, and exact MMSE algorithm in a dispersive channel. |
EAN: 2147483647
Pages: 91
- ERP System Acquisition: A Process Model and Results From an Austrian Survey
- The Second Wave ERP Market: An Australian Viewpoint
- Healthcare Information: From Administrative to Practice Databases
- Relevance and Micro-Relevance for the Professional as Determinants of IT-Diffusion and IT-Use in Healthcare
- Development of Interactive Web Sites to Enhance Police/Community Relations
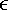

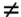 1} and the ambient noise
1} and the ambient noise 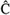
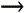
 . Notice that both the LMS algorithm and the DMI algorithm compute the combining weights based only on the signal received during the training period. Since in practice the training period is short compared with the slot length (i.e.,
. Notice that both the LMS algorithm and the DMI algorithm compute the combining weights based only on the signal received during the training period. Since in practice the training period is short compared with the slot length (i.e.,