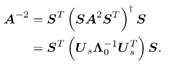4.10 Appendix
4.10 Appendix4.10.1 Proof of Proposition 4.1 in Section 4.4We follow the technique used in [203] by defining the function Equation 4.184
Notice that Equation 4.185
Equation 4.186
Equation 4.187
Equation 4.188
where (4.188)
Equation 4.189
we obtain Equation 4.190
Assume that the penalty function
r
(
x
) is convex and bounded from below; then the cost function
C
(
q
) is convex and has a unique minimum
C
(
q
*). Therefore,
q
* is the unique solution to (4.15) such that
z
(
q
*) =
. Since the sequence
C
(
q
l
) is
Equation 4.191
Since for any realization of
r
, the probability that
z
(
q
l
)
4.10.2 Proof of Proposition 4.2 in Section 4.5
Denote
Equation 4.192
Denote
Equation 4.193
Using (4.192) and (4.193), we obtain Equation 4.194
Equation 4.195
Equation 4.196
where in (4.194)
Equation 4.197
It follows from (4.197) that the
k
th diagonal element
Equation 4.198
|
denotes that the matrix (
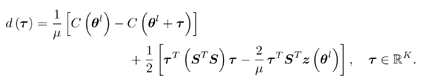
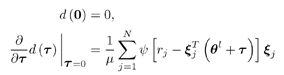
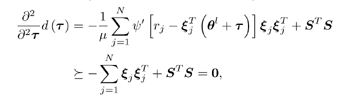
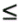
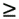0, for any
t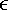
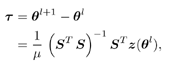
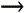
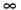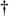. Now on setting
.
. Then (4.75) can be written in matrix form as
. Then from (4.73) and (4.74) we obtain
denotes the Moore “Penrose generalized matrix inverse [189]; in (4.195) we have used the fact that
, which can easily be
; and (4.196) is the matrix form of (4.76). Finally, we notice that
of the diagonal matrix
Chapter 5. Space-Time Multiuser Detection
Section 5.1. Introduction Section 5.2. Adaptive Array Processing in TDMA Systems Section 5.3. Optimal Space-Time Multiuser Detection Section 5.4. Linear Space-Time Multiuser Detection Section 5.5. Adaptive Space-Time Multiuser Detection in Synchronous CDMA Section 5.6. Adaptive Space-Time Multiuser Detection in Multipath CDMA |
5.1 Introduction
It is anticipated that transmit and receive antenna arrays together with adaptive space-time processing techniques will be used in future high-capacity cellular communication systems, to combat interference, time dispersion and multipath fading. There has been a significant amount of recent interest in developing adaptive array techniques for wireless communications (e.g., [48, 154, 356, 570, 571]). These studies have shown that substantial performance gains and capacity
Due to multipath propagation effects and the movement of mobile units, the array steering vector in a multiple-antenna system changes with time, and it is of interest to estimate and track it during communication sessions. One attractive approach to steering vector estimation is to exploit a known portion of the data stream (e.g., the synchronization data stream). For instance, the TDMA mobile radio systems IS-54/136 use 14 known synchronization symbols in each time slot of 162 symbols. These known symbols are very useful for estimating the steering vector and computing the optimal array combining weights. We discuss a number of approaches to adaptive array processing in such systems.
Many advanced signal processing techniques have been proposed for combating interference and multipath channel distortion in CDMA systems, and these techniques fall largely into two categories: multiuser detection (cf. Chapters 1 “4) and space-time processing [370]. Recall that multiuser detection techniques exploit the underlying structure induced by the spreading waveforms of the DS-CDMA
The rest of this chapter is organized as
The following is a list of the algorithms appearing in this chapter.
|
Similar products
- BlackBerry Hacks
Texas hold em king 2 hacker - Pocket PC Network Programming
Pip_adapter_info - Understanding Digital Signal Processing
Finding iir coefficients understanding digital signal processing - Mobile and Wireless Design Essentials
How do you process request through a cell phone to the internet - Microsoft Windows XP Color Management
Printer/postscript color management