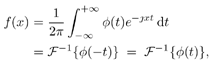4.9 Robust Multiuser Detection in Stable Noise
| So far in this chapter we have modeled non-Gaussian ambient noise using a mixture Gaussian distribution. Recently, the stable noise model has been proposed as a statistical model for the impulsive noise in several applications, including wireless communications [357, 491]. In this section we first give a brief description of the stable distribution. We then demonstrate that the various robust multiuser detection techniques discussed in this chapter are also very effective in combating impulsive noise modeled by a stable distribution. 4.9.1 Symmetric Stable DistributionA symmetric stable distribution is defined through its characteristic function as follows . Definition 4.1: [Symmetric stable distribution] A random variable X has a symmetric stable distribution if and only if its characteristic function has the form Equation 4.165 where Thus, a symmetric stable random variable is completely characterized by three parameters, a , g , and q , where:
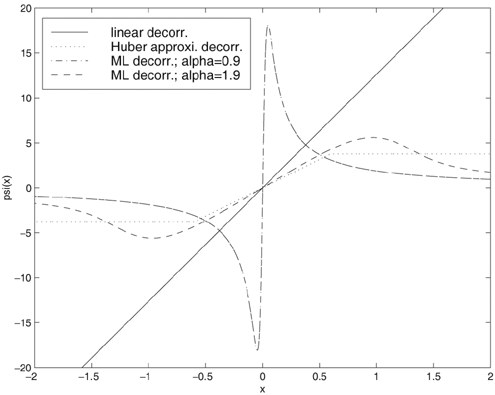
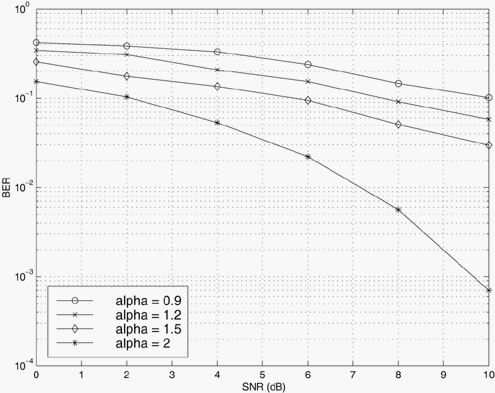
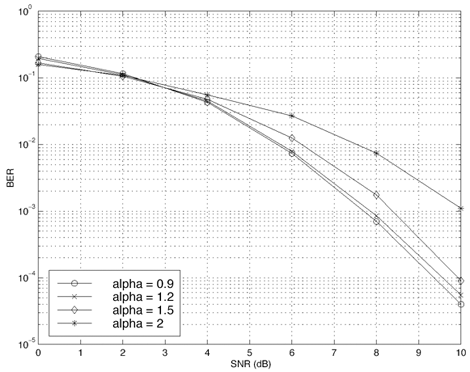
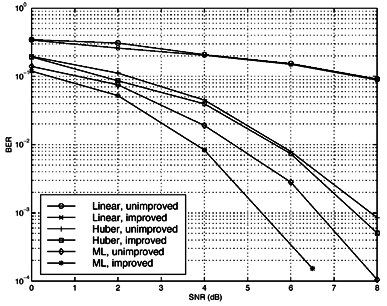
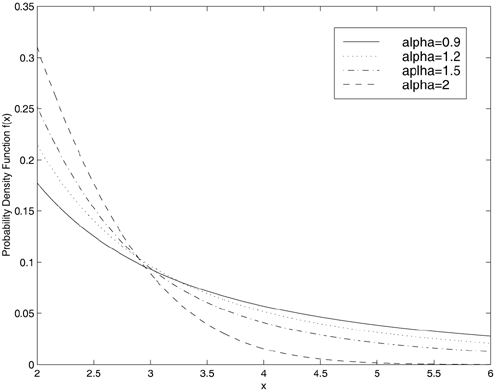
By taking the Fourier transform of the characteristic function, we can obtain the probability density function (pdf) of the symmetric stable random variable X : Equation 4.166 No closed-form expressions exist for general stable pdf's except for the Gaussian ( a = 2) and Cauchy ( a = 1) pdf's. For these two pdf's, closed-form expression exist: Equation 4.167 Equation 4.168 It is known that for a non-Gaussian ( a < 2) symmetric stable random variable X with location parameter q = 0 and dispersion g , we have the asymptote Equation 4.169 where C ( a ) is a positive constant depending on a . Thus, stable distributions with a < 2 have inverse power tails, whereas Gaussian distributions have exponential tails. Hence the tails of the stable distributions are significantly heavier than those of the Gaussian distributions. In fact, the smaller is a , the slower does its tail drop to zero, as shown in Figs. 4.15 and 4.16. Figure 4.15. Symmetric stable pdf's for different values of a . g = 1. Figure 4.16. Tails of the symmetric stable pdf's for different values of a . g = 1. As a consequence of (4.169), stable distributions do not have second-order moments except for the limiting case of a = 2. More specifically , let X be a symmetric stable random variable with characteristic exponent a . If 0 < a < 2, then Equation 4.170 If a = 2, then Equation 4.171 for all m Generation of Symmetric Stable Random VariablesThe following procedure generates a standard symmetric stable random variable X with characteristic exponent a , dispersion g = 1 and location parameter q = 0 (see [357]): Equation 4.172 Equation 4.173 Equation 4.174 Equation 4.175 Equation 4.176 Equation 4.177 Equation 4.178 Equation 4.179 Now in order to generate a symmetric stable random variable Y with parameters ( a , g , q ), we first generate a standard symmetric stable random variable X with parameters ( a , 1, 0), using the procedure above. Then Y can be generated from X according to the following transformation: Equation 4.180 4.9.2 Performance of Robust Multiuser Detectors in Stable NoiseWe consider the performance of the robust multiuser detection techniques discussed in previous sections in symmetric stable noise. In particular, we consider the performance of the linear decorrelator, the maximum- likelihood decorrelator, and the Huber decorrelator, as well as their improved versions based on local likelihood search. First, the y functions for these three decorrelative detectors are plotted in Fig. 4.17. For the Huber decorrelator, the variance s 2 , the original definition of y H ( ·) in (4.112), is replaced by the dispersion parameter g . Note that since the pdf of the symmetric stable distribution does not have a closed form, we have to resort to a numerical method to compute y ML ( x ) given by (4.108). In particular, we can use discrete Fourier transform (DFT) to calculate samples of f ( x ) and f '( x ), as follows. Recall that the characteristic function is given by Figure 4.17. The y functions for a linear decorrelator, Huber decorrelator, and maximum-likelihood decorrelator under symmetric stable noise. g = 0.0792. Equation 4.181 The pdf and its derivative are related to the characteristic function through Equation 4.182 Equation 4.183 Hence by sampling the characteristic function f ( t ) and then perform (inverse) DFT, we can get samples of f ( t ) and f '( t ), which in turns give y ML ( x ). First we demonstrate the performance degradation of the linear decorrelator in symmetric stable noise. The BER performance of the linear decorrelator in several symmetric stable noise channels is depicted in Fig. 4.18. Here the SNR is defined as Figure 4.18. BER performance of a linear decorrelator in a -stable noise. N = 31, K = 6. The powers of the interferers are 10 dB above the power of user 1. Figure 4.19. BER performance of a Huber decorrelator in a -stable noise. N = 31, K = 6. The powers of the interferers are 10 dB above the power of user 1. Figure 4.20. BER performance of three decorrelative detectors and their local-likelihood-search versions. N = 31, K = 6, a = 1.2. The powers of the interferers are 10 dB above the power of user 1. |
EAN: 2147483647
Pages: 91
 2 and the median when 0 <
2 and the median when 0 < 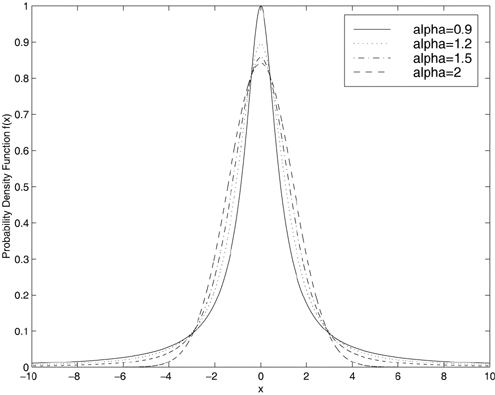
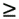 0. Hence for 0 <
0. Hence for 0 <