Irregular Types of Linear Programming Problems
| The basic simplex solution of typical maximization and minimization problems has been shown in this module. However, there are several special types of atypical linear programming problems. Although these special cases do not occur frequently, they will be described within the simplex framework so that you can recognize them when they arise. For irregular problems the general simplex procedure does not always apply. These special types include problems with more than one optimal solution, infeasible problems, problems with unbounded solutions, problems with ties for the pivot column or ties for the pivot row, and problems with constraints with negative quantity values. Multiple Optimal SolutionsConsider the Beaver Creek Pottery Company example with the objective function changed as follows . The graph of this model is shown in Figure A-5. The slight change in the objective function makes it now parallel to the constraint line, 4 x 1 + 3 x 2 = 120. Therefore, as the objective function edge moves outward from the origin, it touches the whole line segment BC rather than a single extreme corner point before it leaves the feasible solution area. The endpoints of this line segment, B and C , are typically referred to as the alternate optimal solutions . It is understood that these points represent the endpoints of a range of optimal solutions. Figure A-5. Graph of the Beaver Creek Pottery Company example with multiple optimal solutions Alternate optimal solutions have the same Z value but different variable values. The optimal simplex tableau for this problem is shown in Table A-25. This corresponds to point C in Figure A-5. Table A-25. The Optimal Simplex Tableau(This item is displayed on page A-25 in the print version)
For a multiple optimal solution the c j z j (or z j c j ) value for a nonbasic variable in the final tableau equals zero. The fact that this problem contains multiple optimal solutions can be determined from the c j z j row. Recall that the c j z j row values are the net increases in profit per unit for the variable in each column. Thus, c j z j values of zero indicate no net increase in profit and no net loss in profit. We would expect the basic variables, s 1 and x 1 , to have zero c j z j values because they are part of the basic feasible solution; they are already in the solution so they cannot be entered again. However, the x 2 column has a c j z j value of zero and it is not part of the basic feasible solution. This means that if some mugs ( x 2 ) were produced, we would have a new product mix but the same total profit. Thus, a multiple optimal solution is indicated by a c j z j (or z j c j ) row value of zero for a nonbasic variable. To determine the alternate endpoint solution, let x 2 be the entering variable (pivot column) and select the pivot row as usual. This selection results in the s 1 row being the pivot row. The alternate solution corresponding to point B in Figure A-5 is shown in Table A-26. Table A-26. The Alternative Optimal Tableau
An alternate optimal solution is determined by selecting the nonbasic variable with c j z j = 0 as the entering variable. An Infeasible ProblemAnother linear programming irregularity is the case where a problem has no feasible solution area; thus, there is no basic feasible solution to the problem. An infeasible problem does not have a feasible solution space. An example of an infeasible problem is formulated next and depicted graphically in Figure A-6. Figure A-6. Graph of an infeasible problem(This item is displayed on page A-26 in the print version) The three constraints do not overlap to form a feasible solution area. Because no point satisfies all three constraints simultaneously , there is no solution to the problem. The final simplex tableau for this problem is shown in Table A-27. Table A-27. The Final Simplex Tableau for an Infeasible Problem(This item is displayed on page A-26 in the print version)
An infeasible problem has an artificial variable in the final simplex tableau. The tableau in Table A-27 has all zero or negative values in the c j z j row, indicating that it is optimal. However, the solution is x 2 = 4, A 1 = 4, and A 2 = 2. Because the existence of artificial variables in the final solution makes the solution meaningless, this is not a real solution. In general, any time the c j z j (or z j c j ) row indicates that the solution is optimal but there are artificial variables in the solution, the solution is infeasible. Infeasible problems do not typically occur, but when they do they are usually a result of errors in defining the problem or in formulating the linear programming model. An Unbounded ProblemIn some problems the feasible solution area formed by the model constraints is not closed. In these cases it is possible for the objective function to increase indefinitely without ever reaching a maximum value because it never reaches the boundary of the feasible solution area. In an unbounded problem the objective function can increase indefinitely because the solution space is not closed. An example of this type of problem is formulated next and shown graphically in Figure A-7. Figure A-7. An unbounded problem In Figure A-7 the objective function is shown to increase without bound; thus, a solution is never reached. A pivot row cannot be selected for an unbounded problem. The second tableau for this problem is shown in Table A-28. In this simplex tableau, s 1 is chosen as the entering nonbasic variable and pivot column. However, there is no pivot row or leaving basic variable. One row value is 4 and the other is undefined. This indicates that a "most constrained" point does not exist and that the solution is unbounded. In general, a solution is unbounded if the row value ratios are all negative or undefined. Table A-28. The Second Simplex Tableau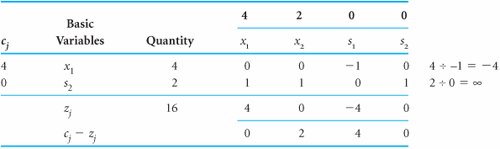 Unlimited profits are not possible in the real world; an unbounded solution, like an infeasible solution, typically reflects an error in defining the problem or in formulating the model. Tie for the Pivot ColumnSometimes when selecting the pivot column, you may notice that the greatest positive c j z j (or z j c j ) row values are the same; thus, there is a tie for the pivot column. When this happens, one of the two tied columns should be selected arbitrarily. Even though one choice may require fewer subsequent iterations than the other, there is no way of knowing this beforehand. A tie for the pivot column is broken arbitrarily. Tie for the Pivot RowDegeneracyIt is also possible to have a tie for the pivot row (i.e., two rows may have identical lowest nonnegative values). Like a tie for a pivot column, a tie for a pivot row should be broken arbitrarily. However, after the tie is broken, the basic variable that was the other choice for the leaving basic variable will have a quantity value of zero in the next tableau. This condition is commonly referred to as degeneracy because theoretically it is possible for subsequent simplex tableau solutions to degenerate so that the objective function value never improves and optimality never results. This occurs infrequently, however. A tie for the pivot row is broken arbitrarily and can lead to degeneracy . In general, tableaus with ties for the pivot row should be treated normally. If the simplex steps are carried out as usual, the solution will evolve normally. The following is an example of a problem containing a tie for the pivot row. For the sake of brevity we will skip the initial simplex tableau for this problem and go directly to the second simplex tableau in Table A-29, which shows a tie for the pivot row between the s 1 and s 3 rows. Table A-29. The Second Simplex Tableau with a Tie for the Pivot Row The s 3 row is selected arbitrarily as the pivot row, resulting in the third simplex tableau, shown in Table A-30. Table A-30. The Third Simplex Tableau with Degeneracy
Note that in Table A-30 a quantity value of zero now appears in the s 1 row, representing the degenerate condition resulting from the tie for the pivot row. However, the simplex process should be continued as usual: s 2 should be selected as the entering basic variable and the s 1 row should be selected as the pivot row. (Recall that the pivot row value of zero is the minimum nonnegative quotient .) The final optimal tableau is shown in Table A-31. Table A-31. The Optimal Simplex Tableau for a Degenerate Problem
Notice that the optimal solution did not change from the third to the optimal simplex tableau. The graphical analysis of this problem shown in Figure A-8 reveals the reason for this. Figure A-8. Graph of a degenerate solution Notice that in the third tableau (Table A-30) the simplex process went to point B , where all three constraint lines intersect. This is, in fact, what caused the tie for the pivot row and the degeneracy. Subsequently, the simplex process stayed at point B in the optimal tableau (Table A-31). The two tableaus represent two different basic feasible solutions corresponding to two different sets of model constraint equations. Degeneracy occurs in a simplex problem when a problem continually loops back to the same solution or tableau. Negative Quantity ValuesOccasionally a model constraint is formulated with a negative quantity value on the right side of the inequality signfor example, 6 x 1 + 2 x 2 Standard form for simplex solution requires positive right-hand-side values. This is an improper condition for the simplex method, because for the method to work, all quantity values must be positive or zero. This difficulty can be alleviated by multiplying the inequality by 1, which also changes the direction of the inequality. A negative right-hand-side value is changed to a positive by multiplying the constraint by -1, which changes the inequality sign. Now the model constraint is in proper form to be transformed into an equation and solved by the simplex method. Summary of Simplex IrregularitiesMultiple optimal solutions are identified by c j z j (or z j c j ) = 0 for a nonbasic variable. To determine the alternate solution(s), enter the nonbasic variable(s) with a c j z j value equal to zero. An infeasible problem is identified in the simplex procedure when an optimal solution is achieved (i.e., when all c j z j An unbounded problem is identified in the simplex procedure when it is not possible to select a pivot rowthat is, when the values obtained by dividing the quantity values by the corresponding pivot column values are negative or undefined. |
EAN: 2147483647
Pages: 358
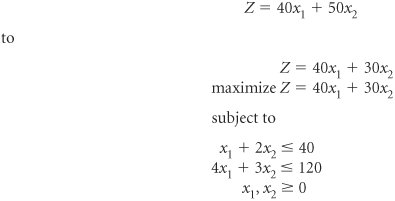



 30
30  0) and one or more of the basic variables are artificial.
0) and one or more of the basic variables are artificial.