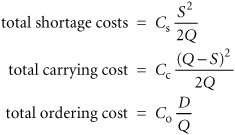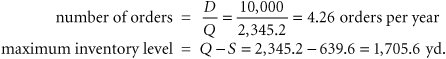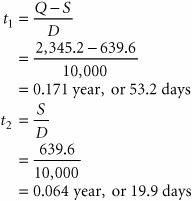The EOQ Model with Shortages
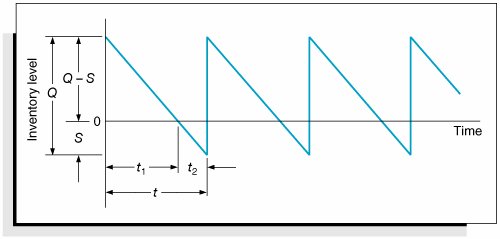
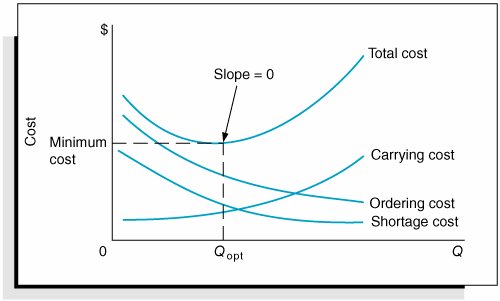
| One of the assumptions of our basic EOQ model is that shortages and back ordering are not allowed. The third model variation that we will describe, the EOQ model with shortages, relaxes this assumption. However, it will be assumed that all demand not met because of inventory shortage can be back ordered and delivered to the customer later. Thus, all demand is eventually met. The EOQ model with shortages is illustrated in Figure 16.7. Figure 16.7. The EOQ model with shortages(This item is displayed on page 743 in the print version) The EOQ model with shortages relaxes the assumption that shortages cannot exist . Because back-ordered demand, or shortages, S , are filled when inventory is replenished, the maximum inventory level does not reach Q , but instead a level equal to Q S . It can be seen from Figure 16.7 that the amount of inventory on hand ( Q S ) decreases as the amount of the shortage increases , and vice versa. Therefore, the cost associated with shortages, which we described earlier in this chapter as primarily the cost of lost sales and lost customer goodwill, has an inverse relationship to carrying costs. As the order size , Q , increases, the carrying cost increases and the shortage cost declines. This relationship between carrying and shortage cost as well as ordering cost is shown in Figure 16.8. Figure 16.8. Cost model with shortages We will forgo the lengthy derivation of the individual cost components of the EOQ model with shortages, which requires the application of plane geometry to the graph in Figure 16.8. The individual cost functions are provided as follows , where S equals the shortage level and C s equals the annual per-unit cost of shortages: Combining these individual cost components results in the total inventory cost formula: You will notice in Figure 16.8 that the three cost component curves do not intersect at a common point, as was the case in the basic EOQ model. As a result, the only way to determine the optimal order size and the optimal shortage level , S , is to differentiate the total cost function with respect to Q and S , set the two resulting equations equal to zero, and solve them simultaneously . Doing so results in the following formulas for the optimal order quantity and shortage level: For example, we will now assume that the I-75 Carpet Discount Store allows shortages and the shortage cost, C s , is $2 per yard per year. All other costs and demand remain the same ( C c = $0.75, C o = $150, and D = 10,000 yd.). The optimal order size and shortage level and total minimum annual inventory cost are computed as follows: Several additional parameters of the EOQ model with shortages can be computed for this example, as follows: The time between orders, identified as t in Figure 16.7, is computed as follows: The time during which inventory is on hand, t 1 in Figure 16.7, and the time during which there is a shortage, t 2 in Figure 16.7, during each order cycle can be computed using the following formulas:
|
EAN: 2147483647
Pages: 358
- ERP Systems Impact on Organizations
- Challenging the Unpredictable: Changeable Order Management Systems
- The Second Wave ERP Market: An Australian Viewpoint
- Enterprise Application Integration: New Solutions for a Solved Problem or a Challenging Research Field?
- A Hybrid Clustering Technique to Improve Patient Data Quality