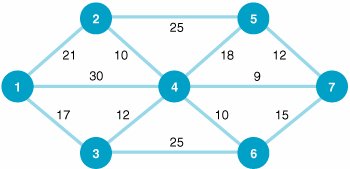
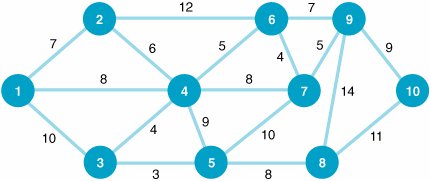
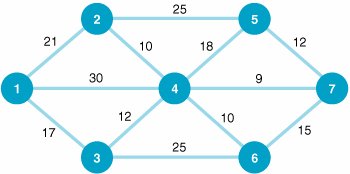
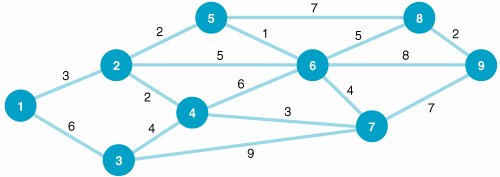
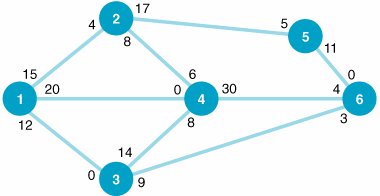
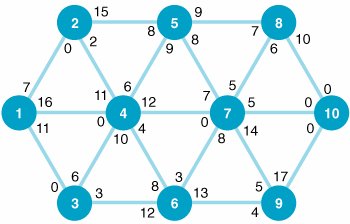
Problems | Introduction to Management Science (10th Edition)

[Page 295]

Given the following network with the indicated distances between nodes (in miles), determine the shortest route from node 1 to each of the other six nodes (2, 3, 4, 5, 6, and 7):

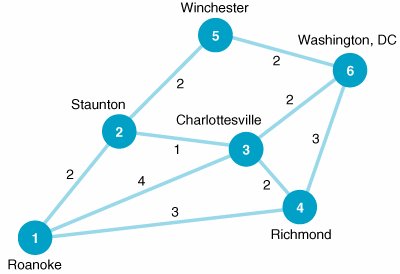
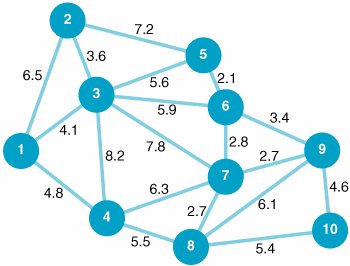
Frieda Millstone and her family live in Roanoke, Virginia, and they are planning an auto vacation across Virginia, their ultimate destination being Washington, DC. The family has developed the following network of possible routes and cities to visit on their trip:

The time, in hours, between cities (which is affected by the type of road and the number of intermediate towns) is shown along each branch. Determine the shortest route that the Millstone family can travel from Roanoke to Washington, DC.

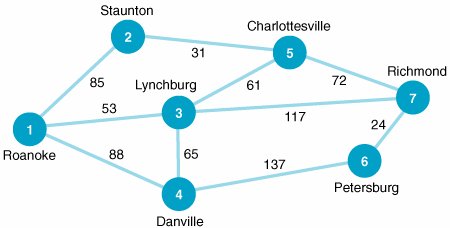
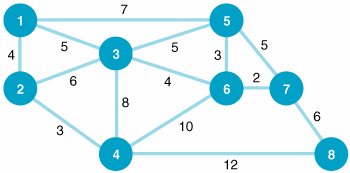
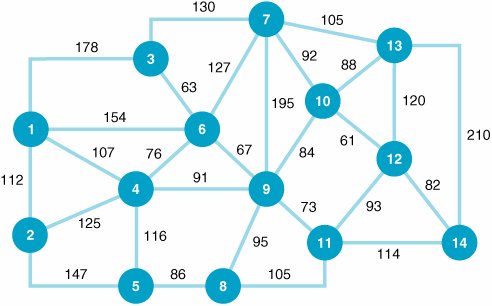
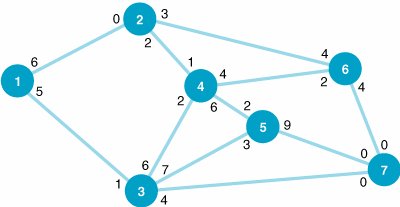
The Roanoke, Virginia, distributor of Rainwater Beer delivers beer by truck to stores in six other Virginia cities, as shown in the following network:

[Page 296]

The mileage between cities is shown along each branch. Determine the shortest truck route from Roanoke to each of the other six cities in the network.

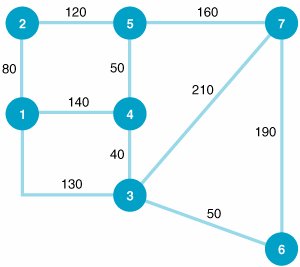
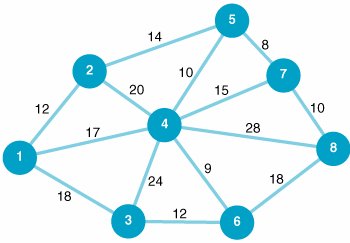
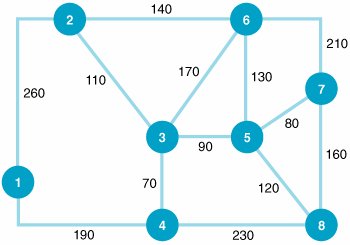
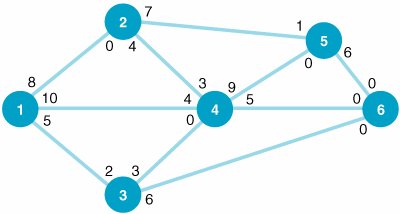
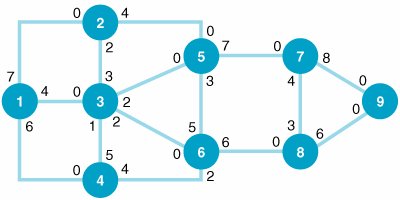
The plant engineer for the Bitco manufacturing plant is designing an overhead conveyor system that will connect the distribution/inventory center to all areas of the plant. The network of possible conveyor routes through the plant, with the length (in feet) along each branch, follows :

Determine the shortest conveyor route from the distribution/inventory center at node 1 to each of the other six areas of the plant.

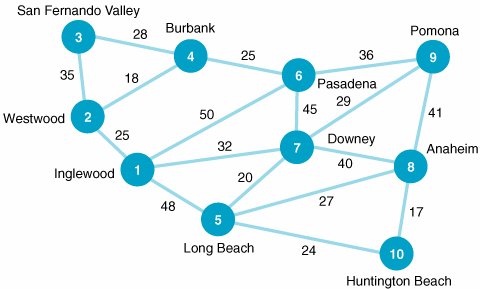
The Burger Doodle restaurant franchises in Los Angeles are supplied from a central warehouse in Inglewood. The location of the warehouse and its proximity, in minutes of travel time, to the franchises are shown in the following network:

Trucks supply each franchise on a daily basis. Determine the shortest route from the warehouse at Inglewood to each of the nine franchises.

[Page 297]

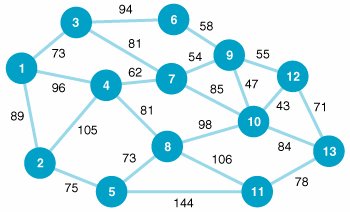
The Petroco gasoline distributor in Jackson, Mississippi, supplies service stations in nine other southeastern cities, as shown in the following network:

The distance, in miles, is shown on each branch. Determine the shortest route from Jackson to the nine other cities in the network.

The Hylton Hotel has a limousine van that transports guests to various business and tourist locations around the city. The following network indicates the different routes the limousine could follow from the hotel at node 1 to the nine locations (nodes 2 through 10):

The values on each branch in the network are the distances, in miles, between the locations. Determine the shortest route from the hotel to each of the nine destinations and indicate the distance for each route.

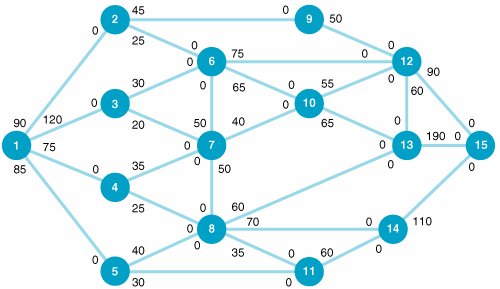
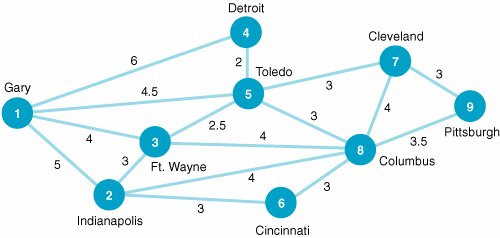
[Page 298]

A steel mill in Gary supplies steel to manufacturers in eight other midwestern cities via truck, as shown in the following network:

The travel time between cities, in hours, is shown along each branch. Determine the shortest route from Gary to each of the other eight cities in the network.

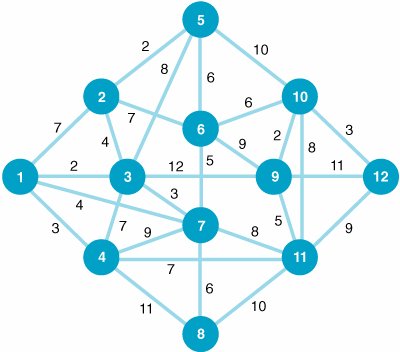
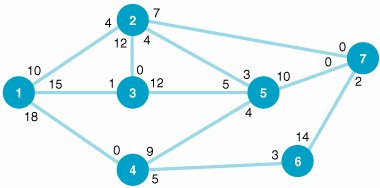
Determine the shortest route from node 1 (origin) to node 12 (destination) for the following network. Distances are given along the network branches:

10.

The members of the Vistas Club are planning a month-long hiking and camping trip through the Blue Ridge Mountains, from north Georgia to Virginia. There are a number of trails through the mountains that connect at various campgrounds, crossings, and cabins. The following network shows the different connecting trails and the distance of each connecting branch, in miles:

[Page 299]

Determine the shortest path from node 1 in north Georgia to node 13 in Virginia and indicate the total mileage of the trail.

11.

Hard Rock Concrete Supply makes concrete at its plant in Centerville, Virginia, and delivers it to construction sites throughout the metropolitan Washington, DC, area. The following network shows the possible routes and distances (in miles) from the concrete plant to seven construction sites:

Determine the shortest route a concrete truck would take from the plant at node 1 to node 8 and the total distance for this route, using the shortest route method.

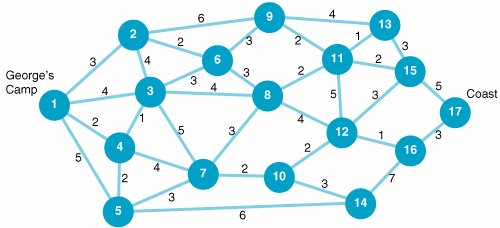
12.

George is camped deep in the jungle , and he wants to make his way back to the coast and civilization. Each of the paths he can take through the jungle has obstacles that can delay him, including hostile natives, wild animals, dense forests and vegetation, swamps, rivers and streams, snakes , insects , and mountains. Following is the network of paths that George can take, with the time (in days) to travel each branch:

[Page 300]

Determine the shortest (time) path for George to take and indicate the total time.

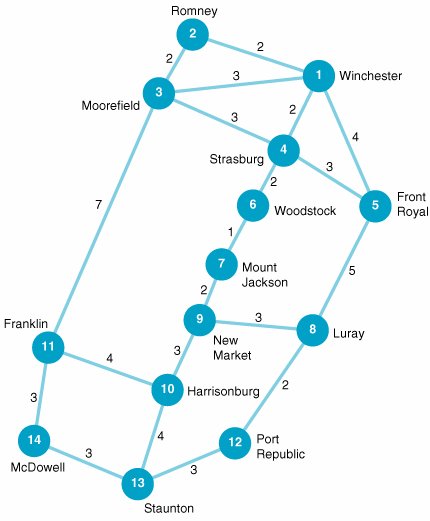
13.

In 1862, during the second year of the Civil War, General Thomas J. "Stonewall" Jackson fought a brilliant military campaign in the Shenandoah Valley in Virginia. One of his victories was at the Battle of McDowell. Using the following figure and your imagination , determine the shortest path and how long it will take (in days) for General Jackson to move his army from Winchester to McDowell to fight the battle:

[Page 301]

14.

The Voyager spacecraft has been transported by an alien being to the Delta Quadrant of space, millions of light- years from Earth. Captain Janeway and her crew are attempting to plot the shortest course home. Following is a network of the possible routes through the Delta Quadrant, where the nodes are different worlds , planetary systems, and space anomalies, and the values on the branches are the actual times, in years, between nodes:

Determine the shortest route from the Voyager's present location (at node 1) to Earth.

15.

John Clooney, a bush pilot in Alaska, makes regular charter flights in his floatplane to various towns and cities in western Alaska. His passengers include hunters, fishermen, backpackers and campers, and tradespeople hired for jobs in the different localities. He also carries some cargo for delivery. The following network shows the possible air routes between various towns and cities John might take (with the times, in hours):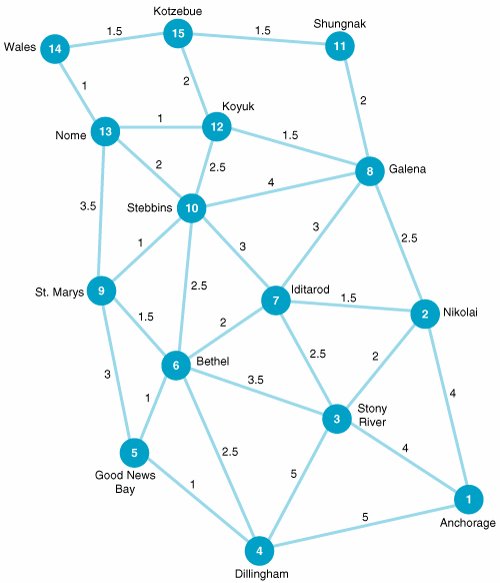

[Page 302]

For safety reasons, he flies point-to-point, at least flying over a town along a route, even though he might not land there. In the upcoming week John has scheduled charter flights for Kotzebue, Nome, and Stebbins. Determine the shortest route between John's home base in Anchorage and each of these destinations.

16.

From 1840 to 1850, more than 12,000 pioneers migrated west in wagon trains. It was typically about a 2,000-mile journey, and pioneers averaged about 10 miles per day. One pioneer family, the Smiths, is planning to join a wagon train traveling west to Oregon. The destination is Fort Vancouver, which is near present-day Portland. The family plans to join a wagon train in St. Louis. However, the trains follow various trails west that are mostly determined by the location of forts and trading posts along the way. The Smith family wants to choose a wagon train that will get them to Oregon in the shortest amount of time. They have checked around with the different wagon train leaders plus immigrants, soldiers, fur traders, and scouts who have previously made the trip west, and from the information they have gathered, they have developed the following network, with estimated times (in days) along each branch: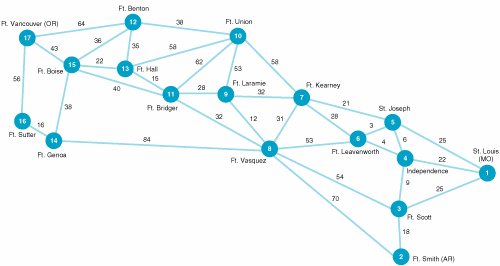

[Page 303]

[Page 304]
Determine the shortest route for the Smiths from St. Louis to Ft. Vancouver.
Another family, the Steins, is leaving from Ft. Smith, Arkansas. Determine the shortest route for the Steins to Ft. Vancouver, Oregon.

17.

A new police car costs the Bay City Police Department $26,000. The annual maintenance cost for a car depends on the age of the car at the beginning of the year. (All cars accumulate approximately the same mileage each year.) The maintenance costs increase as a car ages, as shown in the following table:

Car Age (yr.)	Annual Maintenance Cost	Used Selling Price
	$ 3,000	$
1	4,500	15,000
2	6,000	12,000
3	8,000	8,000
4	11,000	4,000
5	14,000	2,000
6

In order to avoid the increasingly high maintenance costs, the police department can sell a car and purchase a new car at the end of any year. The selling price for a car at the end of each year of use is also shown in the table. It is assumed that the price of a new car will increase $500 each year. The department's objective is to develop a car replacement schedule that will minimize total cost (i.e., the purchase cost of a new car plus maintenance costs minus the money received for selling a used car) during the next 6 years. Develop a car replacement schedule, using the shortest route method.

18.

Given the following network, with the indicated distances between nodes, develop a minimal spanning tree:

19.

A developer is planning a development that includes subdivisions of houses, cluster houses, town- houses , apartment complexes, shopping areas, a daycare center and playground, a community center, and a school, among other facilities. The developer wants to connect the facilities and areas in the development with the minimum number of streets possible. The following network shows the possible street routes and distances (in thousands of feet) between 10 areas in the development that must be connected:

[Page 305]

Determine a minimal spanning tree network of streets to connect the 10 areas, and indicate the total streets (in thousands of feet) needed.

20.

One of the opposing forces in a simulated army battle wishes to set up a communications system that will connect the eight camps in its command. The following network indicates the distances (in hundreds of yards) between the camps and the different paths over which a communications line can be constructed :

Using the minimal spanning tree approach, determine the minimum distance communication system that will connect all eight camps.

21.

The management of the Dynaco manufacturing plant wants to connect the eight major manufacturing areas of its plant with a forklift route. Because the construction of such a route will take a considerable amount of plant space and disrupt normal activities, management wants to minimize the total length of the route. The following network shows the distance, in yards, between the manufacturing areas (denoted by nodes 1 through 8):

[Page 306]

Determine the minimal spanning tree forklift route for the plant and indicate the total yards the route will require.

22.

Several oil companies are jointly planning to build an oil pipeline to connect several southwestern, southeastern, and midwestern cities, as shown in the following network: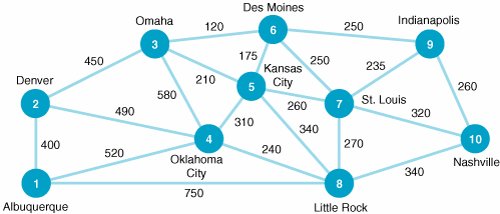

The miles between cities are shown on each branch. Determine a pipeline system that will connect all 10 cities, using the minimum number of miles of pipe, and indicate how many miles of pipe will be used.

23.

A major hotel chain is constructing a new resort hotel complex in Greenbranch Springs, West Virginia. The resort is in a heavily wooded area, and the developers want to preserve as much of the natural beauty as possible. To do so, the developers want to connect all the various facilities in the complex with a combination walkingriding path that will minimize the amount of pathway that will have to be cut through the woods. The following network shows possible connecting paths and corresponding distances (in yards) between the facilities:

Determine the path that will connect all the facilities with the minimum amount of construction and indicate the total length of the pathway.

[Page 307]

24.

The Barrett Textile Mill is remodeling its plant and installing a new ventilation system. The possible ducts connecting the different rooms and buildings at the plant, with the length (in feet) along each branch, are shown in the following network:

Determine the ventilation system that will connect the various rooms and buildings of the plant, using the minimum number of feet of ductwork, and indicate how many feet of ductwork will be used.

25.

The town council of Whitesville has decided to construct a bicycle path that will connect the various suburbs of the town with the shopping center, the downtown area, and the local college. The council hopes the local citizenry will use the bike path, thus conserving energy and decreasing traffic congestion. The various paths that can be constructed and their lengths (in miles) are shown in the following network:

Determine the bicycle pathway that will require the minimum amount of construction to connect all the areas of the town. Indicate the total length of the path.

26.

Determine the minimal spanning tree for the network in Problem 9.

27.

State University has decided to reconstruct the sidewalks throughout the east side of its campus to provide wheelchair access. However, upgrading sidewalks is a very expensive undertaking, so for the first phase of this project, university administrators want to make sure they connect all buildings with wheelchair access with the minimum number of refurbished sidewalks possible. Following is a network of the existing sidewalks on the east side of campus, with the feet between each building shown on the branches:

[Page 308]

Determine a minimal spanning tree network that will connect all the buildings on campus with wheelchair access sidewalks and indicate the number of feet of sidewalk.

28.

Tech wants to develop an area network that will connect its server at its computer and satellite center with the main campus buildings to improve Internet service. The cable will be laid primarily through existing electrical tunnels, although some cable will have to be buried underground . The following network shows the possible cable connections between the computer center at node 1 and the various buildings, with the distances, in feet, along the branches: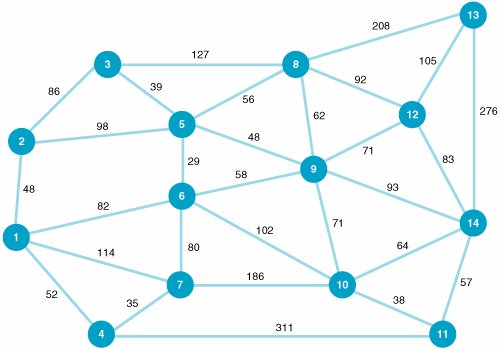

[Page 309]

Determine a minimal spanning tree network that will connect all the buildings and indicate the total amount of cable that will be needed to do so.

29.

Given the following network, with the indicated flow capacities of each branch, determine the maximum flow from source node 1 to destination node 6 and the flow along each branch:

30.

Given the following network, with the indicated flow capacities along each branch, determine the maximum flow from source node 1 to destination node 7 and the flow along each branch:

31.

Given the following network, with the indicated flow capacities along each branch, determine the maximum flow from source node 1 to destination node 6 and the flow along each branch:

[Page 310]

32.

A new stadium complex is being planned for Denver, and the Denver traffic engineer is attempting to determine whether the city streets between the stadium complex and the interstate highway can accommodate the expected flow of 21,000 cars after each game. The various traffic arteries between the stadium (node 1) and the interstate (node 8) are shown in the following network:

The flow capacities on each street are determined by the number of available lanes, the use of traffic police and lights, and whether any lanes can be opened or closed in either direction. The flow capacities are given in thousands of cars. Determine the maximum traffic flow the streets can accommodate and the amount of traffic along each street. Will the streets be able to handle the expected flow after a game?

33.

The FAA has granted a license to a new airline, Omniair, and awarded it several routes between Los Angeles and Chicago. The flights per day for each route are shown in the following network:

Determine the maximum number of flights the airline can schedule per day from Chicago to Los Angeles and indicate the number of flights along each route.

34.

The National Express Parcel Service has established various truck and air routes around the country over which it ships parcels. The holiday season is approaching, which means a dramatic increase in the number of packages that will be sent. The service wants to know the maximum flow of packages it can accommodate (in tons) from station 1 to station 7. The network of routes and the flow capacities (in tons of packages per day) along each route are shown in the following network:

[Page 311]

Determine the maximum tonnage of packages that can be transported per day from station 1 to station 7 and indicate the flow along each branch.

35.

The traffic management office in Richmond is attempting to analyze the potential traffic flow from a new office complex under construction to an interstate highway interchange during the evening rush period. Cars leave the office complex via one of three exits, and then they travel through the city streets until they arrive at the interstate interchange. The following network shows the various street routes (branches) from the office complex (node 1) to the interstate interchange (node 9):

All intermediate nodes represent street intersections, and the values accompanying the branches emanating from the nodes represent the traffic capacities of each street, expressed in thousands of cars per hour. Determine the maximum flow of cars that the street system can absorb during the evening rush hour .

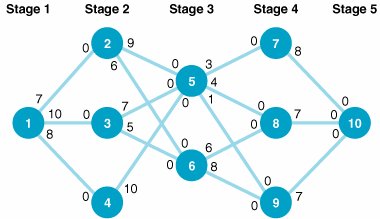
36.

The Dynaco Company manufactures a product in five stages. Each stage of the manufacturing process is conducted at a different plant. The following network shows the five different stages and the routes over which the partially completed products are shipped to the various plants at the different stages:

[Page 312]

Stage 5 (at node 10) is the distribution center in which final products are stored. Although each node represents a different plant, plants at the same stage perform the same operation. (For example, at stage 2 of the manufacturing process, plants 2, 3, and 4 all perform the same manufacturing operation.) The values accompanying the branches emanating from each node indicate the maximum number of units (in thousands) that a particular plant can produce and ship to another plant at the next stage. (For example, plant 3 has the capacity to process and ship 7,000 units of the product to plant 5.) Determine the maximum number of units that can be processed through the five-stage manufacturing process and the number of units processed at each plant.

37.

Suppose in Problem 36 that the processing cost per unit at each plant is different because of different machinery, workers' abilities , overhead, and so on, according to the following table:

Stage 1	Stage 2	Stage 3	Stage 4
1. $3	2.$5	5.$22	7.$12
	3.7	6.19	8.14
	4.4		9.16

There are no differentiated costs at stage 5, the distribution center. Given a budget of $700,000, determine the maximum number of units that can be processed through the five-stage manufacturing process.

38.

Given the following network, with the indicated flow capacities along each branch, determine the maximum flow from source node 1 to destination node 10 and the flow along each path:

[Page 313]

39.

A manufacturing company produces different variations of a product at different work centers in its plant on a daily basis. Following is a network showing the various work centers in the plant, the daily capacities at each work center, and the flow of the partially completed products between work centers:

Node 1 represents the point where raw materials enter the process, and node 15 is the packaging and distribution center. Determine the maximum number of units that can be completed each day and the number of units processed at each work center.

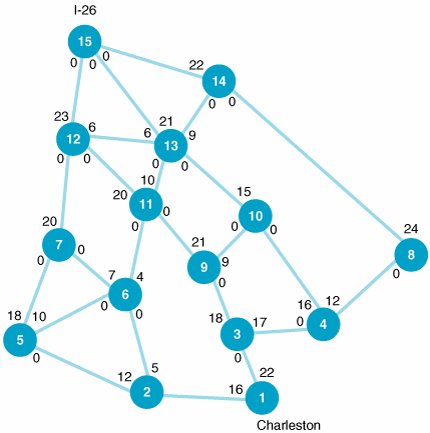
40.

The following network shows the major roads that would be part of the hurricane evacuation routes for Charleston, South Carolina:

[Page 314]

The destination is the interchange of Interstate 26 and Interstate 526, north of Charleston. The nodes represent road intersections, and the values at the nodes are the traffic capacities, in thousands of cars. Determine the maximum flow of cars that can leave Charleston during a hurricane evacuation and the optimal flow along each road segment (branch 1).

41.

In Problem 41 in Chapter 6, KanTech Corporation ships electronic components in containers from seaports in Europe to U.S. ports, from which the containers are transported by truck or rail to inland ports and then transferred to an alternative mode of transportation before being shipped to KanTech's U.S. distributors . Using the shipping capacity at each port, develop a maximal flow network to determine the number of containers to ship through each port to meet demand at the distribution centers.