Example Problem Solution
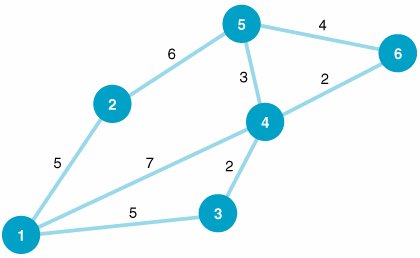
| Step 1. | (Part A): Determine the Shortest Route Solution
The shortest route network follows : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
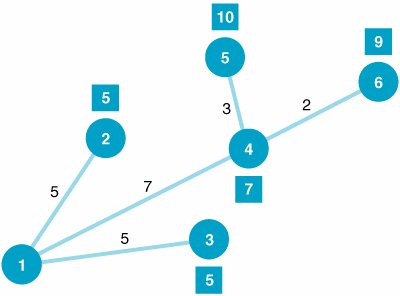
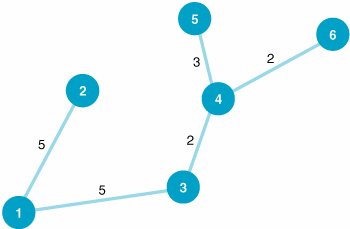
| Step 2. | (Part B): Determine the Minimal Spanning Tree
|
EAN: 2147483647
Pages: 358
- Challenging the Unpredictable: Changeable Order Management Systems
- ERP System Acquisition: A Process Model and Results From an Austrian Survey
- Context Management of ERP Processes in Virtual Communities
- Healthcare Information: From Administrative to Practice Databases
- Relevance and Micro-Relevance for the Professional as Determinants of IT-Diffusion and IT-Use in Healthcare