10.5 Pricing contingent claims
10.5 Pricing contingent claims
The binomial lattice used to price contingent claims is characterised as follows :
| C | ˆ’ | interest rate contingent claim, |
| C ( n, i ) | ˆ’ | unique price of the contingent claim defined at each node( n, i ), |
| T | ˆ’ | expiry time of the contingent claim, |
| { f ( i )} | ˆ’ | set of payoffs of the contingent claim at expiry 0 ‰ i ‰ T (since at each time n there are ( n + 1) states, hence at time T there are ( T + 1) possible payoff values). Therefore the terminal condition is C ( T,i ) = f ( i ), 0 ‰ i ‰ T , |
| L ( n, i ), U ( n, i ) | ˆ’ | lower and upper bounds on the contingent claim price such that L ( n, i ) ‰ C ( n, i ) ‰ U ( n, i ), |
| X ( n, i ) | ˆ’ | amount paid by the contingent claim at time n , state i , 1 ‰ n ‰ T . |
10.5.1 No arbitrage contingent claim price.
Let V be the value of a risk-free portfolio made up of one discount bond with maturity T and ¾ of asset C . Consider the time n , state i value of the portfolio:
This portfolio is subject to an upstate move. Hence the price of the discount bond becomes:
and the value of the portfolio may be expressed as:
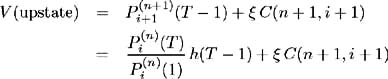
Similarly, if the portfolio is subject to a downward move its value is:
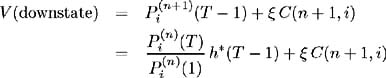
By definition the portfolio is risk-free and so V (upstate) = V (downstate). Therefore, the amount of asset C required to ensure a risk-free portfolio is calculated as:
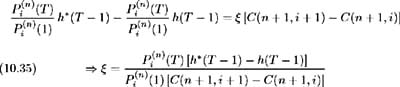
Given this value of ¾ the portfolio is risk-free over one period and hence must earn the risk-free rate of return, 1/ P ( n ) i (1):
and making use of (10.35), (10.22) and (10.23) we may solve for the time n , state i price of the contingent claim as a function of the possible contingent claim prices at time ( n + 1):

Now the contingent claim may be priced by backward induction. We know the value of the contingent claim in all states i at expiry time T . The price of the contingent claim in each state i one period prior to expiry i.e. C *( T ˆ’ 1, i ) is determined from equation (10.36). This calculated price is subject to the pre-specified boundary conditions; hence:
Iteration of this methodology produces the initial price of the contingent claim. Knowledge of the implied binomial probability and the one period discount bond price P ( n ) i (1), at each time n , state i , allows us to price any interest rate contingent claim. We conclude that the pricing depends on the stochastic evolution of the short- term interest rate and so this model may also be referred to as a one factor model.
The parameters and are not directly observable in the term structure, but are reflected in the valuation of contingent claims. An estimation procedure may be used to ensure a best fit of the model-generated (theoretical) contingent claim prices to actual observed prices. Since and are characteristics of the term structure and not of the specific contingent claim, the estimated parameter values may be used to price any contingent claim.
EAN: 2147483647
Pages: 132