4.3 Option pricing
4.3 Option pricing
LS [ 38 ] derive an analytical formula for the value of a European option on a default-free discount bond. The option value is derived from within the equilibrium framework and is hence a function of the two factors determining discount bond prices. The explicit dependence on the current interest rate volatility is a desirable characteristic, since volatility is one of the key determinants of option values.
Let C ( r, V, ; K, T ) be the price of a European call option with maturity , strike price K , on a discount bond with term to maturity + T . Since the value of this call option must satisfy the fundamental pricing equation (4.6), LS show the closed-form solution to be:
where ( ·) is the bivariate non-central chi-square distribution and 1 , 2 , 3 , 4 , ‰ 1 , ‰ 2 , ‰ 3 and ‰ 4 are functions of the parameters of the underlying state variables . Since the two variates of each bivariate distribution are independent, the joint density is a product of the individual densities of the two variates, each being non-central chi-square [11] .
Since the variance of the interest rate follows a stochastic process, this model allows option pricing with stochastic volatility. This is one of the few interest rate option models allowing for closed-form solutions with stochastic volatility [ 45 ].
To extend this methodology, LS [ 39 ] use a separation of variables technique to incorporate the initial observed term structure. This extended model incorporates actual discount functions to determine the initial option prices. This means that it cannot be used to price simple discount bonds . However, all other European interest rate contingent claims may be valued.
Consider the value of a European default-free contingent claim H ( x, y, ), with payoff at maturity H ( x, y, 0) = G ( x, y ). (The contingent claim is a function of the transformed, unobservable state variables x and y .) The value of this contingent claim may be factorised into its forward value and a discount function, with the same maturity date as the contingent claim:
where P ( x, y, ) is a discount bond and M ( x, y, ) the forward value of the contingent claim. Calculating all required partial derivatives we rewrite (4.6) as:
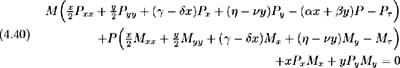
However, since P ( x, y, ) also satisfies (4.6), we have:
and (4.40) becomes:
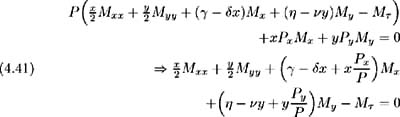
with terminal boundary condition M ( x, y, 0) = G ( x, y ). The terms dependent on the price of the discount bond, P x /P and P y /P , can be evaluated from (4.25) as:
and hence the forward value of a European contingent claim may be found by solving (4.41) subject to an appropriate terminal boundary condition. The present value of this contingent claim is found by discounting the forward price by the unit discount bond (with appropriate maturity) observable from the current term structure.
From (4.41) we may consider the forward value of the contingent claim M ( x, y, ), to be the expected value of the terminal payoff G ( x, y ), hence:
where the expectation is taken over the joint probability distribution of x and y implied by the risk adjusted processes:
The two processes above are square root processes, much like in the CIR model, and hence produce distributions related to the non-central chi-square distribution. Since x and y are independent, the joint distribution (the bivariate, non-central chi-square distribution) is a product of the two distributions.
The advantage of this extension to the model is that all information from the current term structure, as well as dynamics of the state variables are incorporated in the pricing. However, this approach loses the general equilibrium consistency, since not all discount bond prices are endogenously determined.
[11] For details of the non-central chi-square distribution, see Chapter 2 on the CIR model.
EAN: 2147483647
Pages: 132
- Chapter IV How Consumers Think About Interactive Aspects of Web Advertising
- Chapter VIII Personalization Systems and Their Deployment as Web Site Interface Design Decisions
- Chapter XII Web Design and E-Commerce
- Chapter XVI Turning Web Surfers into Loyal Customers: Cognitive Lock-In Through Interface Design and Web Site Usability
- Chapter XVIII Web Systems Design, Litigation, and Online Consumer Behavior