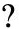Number Crunching Mathematical and Relational Operators and Commands

This chapter is all about number crunching, which is another way of referring to mathematical and relational programming. These are very important features that you will need to write useful programs. While the basic math operations of addition, subtraction, multiplication, and division are supported in all programming languages, DarkBASIC also has support for exponents and trigonometry. DarkBASIC makes it easy and fun to write math programs. While learning these new tricks, you'll learn about random numbers, reading date and time, and using relational operators (greater than, equal to, less than, and so on). Along the way, I'll show you how to extend these commands by adding functionality of your own.

Mathematical Operators

DarkBASIC provides a good assortment of mathematical operators that you can use in your programs. These operators are built into the language. The basic math operations for performing addition, subtraction, multiplication, and division, as well as working with exponents, are a common feature of all programming languages, so you can use what you learn in DarkBASIC with other languages as well.

Addition

The plus sign is used to add numbers (integers or decimals) from one or more variables, including for variable assignment and formulas used in branching statements. Addition is commonly used to increment the value of a counter variable, as shown in this example.

REM Initialize the variable
N = 0
REM Increment the variable
N = N + 10

Remember, it is good programming practice to declare all variables before you use them, even if DarkBASIC doesn't require you to do so. There's no rule stating that you must set N to 0 before incrementing it. However, it is just good practical sense, not to mention very helpful when you are modifying the program later. I have written many programs when I was in a hurry and didn't comment my code enough. Coming back to a poorly written program is very difficult because months later you won't remember how the program works! DarkBASIC automatically sets numbers to zero upon initialization, but I always initialize variables. This has the added benefit of helping someone down the road understand how the program works.

The last line, N = N + 10, is called a formula because the variable on the left side is assigned the results of the right side, which is the formula N + 10.

Using Return Values in a Formula

You could just as easily use a function to return a number that is assigned to the variable, as shown in the following code.

REM Create a function
FUNCTION Twelve()
 Number = 12
ENDFUNCTION Number

REM Initialize a variable
N = 0

REM Add the function value to the variable
N = N + Twelve()

Now, suppose you try to add some letters to a number. What do you think will happen? Because the variable N was created as a number, the DarkBASIC compiler will complain if you try to add some text to the number variable. For example, this code:

N = 0
N = 10 + "ABC"

will generate a compiler error message like this:

Syntax Error. Unrecognized parameter at line 2

DarkBASIC was expecting to see another number to add to the variable N but instead it got a string, so it didn't know what to do! You can, in fact, add strings together just like you can numbers, but you have to declare a string with the dollar sign character ($). For example, the following code is a valid program.

D$ = "Dark"
D$ = D$ + "BASIC"
PRINT D$

The INC Command

The INC command in DarkBASIC is quite useful; it increments a variable by a specified value. If you just want to increment a variable by 1, you can leave the value parameter blank. In the following example, the answer reported by DarkBASIC is 30.

Num = 10
INC Num,
20 PRINT Num

Subtraction

Subtraction is also so simple that it hardly requires explanation. Unlike addition, however, you can't subtract one string from another. You can obviously subtract numbers, but strings can only be appended together, using the convenient + operator. Following is an example of how to subtract two numbers.

N = 100
P = 75
N = N - P
PRINT N

Subtracting Multiple Numbers

You can also subtract more than two numbers. You can actually have as many subtractions in a single formula as you want, within reason. Here's another example:

A = 100
B = -10
C = 1972
D = 1939492
E = -100
N = A - B - C - D - E - 200
PRINT N

What do you think the answer to this problem is? Well, go ahead and type it into DarkBASIC and see what answer it returns. Don't be surprised if the answer is a large negative number (thanks to the D variable).

Quick Subtraction

Let me show you a quick way to subtract large numbers in your head, because this is a valuable tool for counting change, especially if you work in a retail store. You will also amaze your friends after learning how to do it. What's the most common type of change returned? Change for a one-dollar bill, a ten-dollar bill, or a twenty-dollar bill, right? Multiples of 10 are difficult to use because 10 has two digits, which makes it hard to carry over the number from 10. However, it's really easy to subtract with a 9 because there is no number to carry.

Here's an example. A customer's total bill is $8.37, and he hands you a ten-dollar bill. The change is $1.63, and I came up with that in only a couple seconds in my head. You're thinking, "Yeah, right. You used a calculator." Not at all! Let me show you how I did it. Change the 10.00 into 9.99 in your head. Subtract 9-8, and you get 1. Subtract 9-3, and you get 6. Subtract 9-7, and you get 2. The key is to always remember to add one to the final answer, since you were using nines.

Figure 8.1 shows the old-school way of doing subtraction, and Figure 8.2 shows the faster method.

Figure 8.1: In old-school subtraction problems, you must borrow and carry digits.

Figure 8.2: The faster method of subtraction using nines

Of course, this method works with more than just money. Any number that can be broken down into easy-to-use nines will work with this technique.

The DEC Command

The DEC command is a useful way to decrement a value from a variable. If you just want to do a simple decrement by 1, leave the value parameter blank. The following example demonstrates the DEC command; the answer reported by DarkBASIC is 80.

Num = 100
DEC Num, 20
PRINT Num

Multiplication

Multiplication was derived from addition, and it can be put into a table for easy memorization. I'm sure you memorized multiplication tables in elementary school, like most kids. The ability to quickly multiply numbers in your head is invaluable in day-to-day life. But for larger numbers, it's not as easy. Any number larger than 12 will stump the vast majority of us, and that is where a calculator comes in handy. Like most programming languages, DarkBASIC uses the asterisk character (*) for multiplication. Here is an example:

A = 27
B = 19
C = A * B

How about a real-world example? The circumference of a circle is the distance around the circle, as if you were to wrap a measuring tape around your waist to get measurements for a new suit or dress. To calculate the circumference of a circle, you multiply two times the radius times [.pi] (Pi, a Greek character that is pronounced like pie), or C = 2[.pi]r. Expressed in DarkBASIC source code, here is how you can calculate circumference.

PI# = 3.14159265
Radius# = 6
Circumference# = 2 * PI# * Radius#
PRINT "Circumference = "; Circumference#
This program produces the following output.
Circumference = 37.6991

This brings up an important point about the types of data that can be stored in your variables. Did you notice the pound sign (#) after each of the variables in the previous code listing? That tells DarkBASIC that those are decimal numbers. If you omit the pound sign anywhere a variable is used, DarkBASIC will treat it as an integer and you will lose any decimal places that were part of the number. In the case of the previous listing, it's essential that the variables have decimal places, or else DarkBASIC will fail to calculate the circumference of the circle properly. Just remember that you have to use the pound sign every time the variable is used, just like you have to use the dollar sign every time you use a string variable in the program.

Division

The average human mind can handle addition, subtraction, and multiplication pretty well (at least with small numbers), but for some reason, most people have trouble with division. Division used to be problematic for computers too, because it requires a lot more work than multiplication. Of course, this means that a computer might have been able to do ten million divisions per second versus one hundred million additions, subtractions, or multiplications. Fortunately, modern processors are now optimized to handle division quickly and efficiently, which is part of the reason why 3D graphics are so amazing today. (Another reason why we have such great 3D games today is that modern processors are able to handle decimals just as easily as integers.)

In general, you don't need to worry about how long a math calculation will take because all of the really speed-intensive stuff is built into DarkBASIC. At best, your DarkBASIC programs are scripts that the engine runs, which are not limited in speed by one data type or another. Now let me give you a simple example of integer division.

A = 5000
B = 1000
C = A / B
PRINT "C = "; C

Here is another example of a division operation, this time using a decimal number. This short program converts a temperature from Fahrenheit to Celsius.

Fahren# = 30
Celsius# = 5 * (Fahren# - 32) / 9
PRINT Fahren#; " F = "; Celsius#; " C"

Exponentiation

There is another basic math operator in DarkBASIC that can be very useful. The exponent operator (∧) is the Shift-6 character. An exponent is a number raised to a power, which means that number is multiplied by itself a given number of times. For example, 1010=100, while 101010=1000. The exponent character lets you quickly calculate an exponent. For example, suppose you wanted to calculate 57 to the power of 8. You could write a program that calculates the power of a number the hard way, as follows.

Number = 57
Result = Number
FOR N = 1 TO 7
 Result = Result * Number
NEXT N
PRINT "Answer = "; Result

Note that the loop steps from 1 to 7 because the first calculation starts with 2 in an exponent, such as Number * Number. DarkBASIC prints out the following answer.

Answer = 106450183

That's a whopping big number! Be careful when using exponents because seemingly small numbers raised to a power suddenly become enormous. Also, be careful not to calculate a number that is too big for the variable to handle. DarkBASIC variables have a large range, in the billions, but a number can easily get into the billions when you use exponents. Here's the same calculation using the exponent operator instead.

Number = 57
Result = Number ^ 8
PRINT "Answer = "; Result

This simple example shows why it is helpful to learn all of the features in DarkBASIC before attempting to solve a problem the hard way. Check the PDF on the CD, DarkBASIC Language Reference, for a reference of DarkBASIC commands and data types.

Relational Operators

The human mind is extremely adept at seeing the differences and relationships between individual things and among groups of things, such as the classic example of individual trees in a forest (also an individual thing). By simply driving through a forest, you can tell at a glance what types of trees make up the forest, such as pines, oaks, and spruces. This ability is called pattern recognition, and it is the basis for memory.

Computer programs do not have our ability to instantly come to a conclusion with limited information. We are able to see part of a pattern and imagine the rest of it, thus determining what an object is by seeing merely part of it. Computers are not very good at pattern recognition—yet!—and they must evaluate differences at both highly detailed and lower levels. For instance, a human might look at two cars and note that they are absolutely identical. But a computer might examine the same two cars and find that they are made of different components or built in different years. A computer might even point out flaws in the paint. As a result, computers are able to examine things with great precision, something we humans are incapable of doing. In time, emerging technologies such as adaptive neural networks will enable computers to reach human-level pattern recognition.

This technology has already been put into practical use for speech and character recognition. Indeed, computers that are capable of listening to human speech and understanding the scratches we call human written language make an impression on humans that is often eerily lifelike. These basic faculties that have set us somehow above the raw processing power of computers have given many of us an air of superiority. When confronted with computers that seem to have similar behavior— by merely exhibiting pattern recognition—the implications can be somewhat frightening to those not directly involved in the computer industry. Give a computer pattern recognition and limited conversational programming, and the result is startlingly human-like.

While neural networks and artificial intelligence are fascinating subjects, as a programmer you will need to master a few basic concepts before you attempt to bring a computer to life. For one thing, you need to understand how to give a program some simple logic because logic is what gives a program the ability to work with data. To add logic to your programs, you need to use something called a relational operator.

Relational operators deal with how values compare to each other, or rather, how they relate to each other. Relational operators are usually found within formulas that result in a Boolean (true or false) value, and are based on simple rules: equal to, not equal to, greater than, and less than. Data types determine the way objects relate to one another. Variables of the same data type can be evaluated against each other, but variables of different data types cannot be compared using a relational operator. For example, you can't compare "1" with 1 because the first number is actually a string (with quotes). To make a comparison of this sort, you need to convert the string to a number, which applies only if the string actually contains a valid number.

The following sections cover the actual operators used to perform relational comparisons, along with a description of how to use each one. Table 8.1 provides a quick reference of these operators.

Table 8.1: Relational Operators

Operator	Description
=	Equal to
<>	Not equal to
<	Less than
>	Greater than
<=	Less than or equal to
>=	Greater than or equal to

Equal To

The equal to operator (=) tests for the equality of two values in a formula. The equals sign also assigns values to variables, but DarkBASIC can tell the difference. Here is an example of a test for an equal condition:

IF A = B
 PRINT "A is equal to B"
ELSE
 PRINT "A is not equal to B"
ENDIF

Not Equal To

To test for inequality, use the not equal to operator (<>), which is the opposite of the equal to operator. Here is an example:

IF A <> B
 PRINT "A is not equal to B"
ELSE
 PRINT "A is equal to B"
ENDIF

Less Than

The less than operator (<) returns true when the first operand is less than the second operand in a formula. Keep in mind that this applies to any data type. You could even compare two strings; if the ASCII values of the first string are less than the ASCII values of the second string, then the less than comparison will return true. Here is an example:

IF A < B
 PRINT "A is less than B"
ELSE
 PRINT "A is not less than B"
ENDIF

Greater Than

The greater than operator (>) returns true when the first operand is greater than the second operand in a formula, as the following example demonstrates.

IF A > B
 PRINT "A is greater than B"
ELSE
 PRINT "A is not greater than B"
END IF

Less Than or Equal To

The less than or equal to operator is a combination of two other operators—equal to (=) and less than (<). Here is an example:

IF A <= B
 PRINT "A is less than or equal to B"
ELSE
 PRINT "A is not less than or equal to B"
ENDIF

Remember that combining two operators in this way is the same as checking each one separately. You could accomplish the same result by creating a formula that combines both operators using the logical OR operator, as follows.

IF A < B OR A = B
 PRINT "A is less than or equal to B"
ELSE
 PRINT "A is not less than or equal to B"
ENDIF

Greater Than or Equal To

The last relational operator, greater than or equal to, is also a combination of two operators—greater than (>) and equal to (=). Here is an example:

IF A >= B
 PRINT "A is greater than or equal to B"
ELSE
 PRINT "A is not greater than or equal to B"
ENDIF

Just like in the previous example, you can accomplish the same thing by writing a compound relational formula, such as this:

IF A > B OR A = B
 PRINT "A is greater than or equal to B"
ELSE
 PRINT "A is not greater than or equal to B"
ENDIF

Basic Math Commands

DarkBASIC has several useful math commands; I will go over the basic ones here. I'll explain the more advanced math commands later in this chapter.

The SQRT Command

The SQRT command is short for "square root." The square root of a number X is the value which, when multiplied by itself, results in the number X. The square root is the opposite of a number raised to the second power (N ∧ 2). Consider an earlier example, 1010=100. The square root of 100 is 10, or rather, SQRT(100) = 10.

Remember that this differs from exponents in general in that the square root only applies to a squared number. Here is an example:

A = 100
B = SQRT(A)
PRINT "The square root of "; A; " is "; B; "."

The ABS Command

The ABS command returns the absolute value of a number that is passed as a parameter. The absolute value is simply the positive magnitude of any number. For example, ABS(5) = ABS(−5) = 5. You will use this command often when you are certain that a negative value would be detrimental to the outcome of a formula, such as when calculating the circumference of a circle. In the unusual event that a radius value is negative, you would use the ABS command to ensure a positive value before performing the calculation.

The INT Command

The INT command returns the largest integer before the decimal point of a floatingpoint number. In other words, when passed as a parameter to INT, the decimal portion of the number is simply dropped.

The EXP Command

The EXP command returns a result raised to the power of a number (both of which must be integers).

Random Numbers

You often need a random number to mix up something, such as a virtual deck of cards or pair of dice. Random numbers are frequently used in games to keep the game play interesting from one scene to the next. Randomness is also a factor when you are dealing with data encryption and compression, as well as in simulation programs (such as business and financial simulations). For example, suppose you want to move an enemy ship around the screen to attack a player. It is more of a challenge if the enemy ship moves from place to place in an unpredictable manner instead of a predetermined manner; random numbers can help you accomplish this.

Creating Random Numbers

DarkBASIC provides an easy-to-use random number generator called RND, which returns an integer. When using RND, the important thing to remember is that it generates a range of random numbers from 0 to the passed parameter value. While some programming languages will return a number from 0 to N-1 (that is, one less than the passed value), DarkBASIC generates random numbers from 0 to the actual value passed to it. That means RND(5) could result in 0, 5, or anything between the two. Following are some examples of possible random numbers generated with RND.

RND(2000) = 1039
RND(1000000) = 9329193
RND(20) = 18

As you can see, these numbers all fall between 0 and the passed value. If you want to exclude 0 from the result, you need to subtract 1 from the passed value, and then add 1 to the returned value. Here's some code that simulates rolling a six-sided die:

Num = RND(6 - 1) + 1

Why pass 6 - 1 to RND? Since there is no zero on a die, you need to add 1 to the final result. But that means the answer could be from 1 to 7. Obviously, you would want to write the code like this:

Num = RND(5) + 1

However, it might be even more convenient to write a function that returns a random number based on one rather than zero (which is useful in real-world programs, such as ones that simulate the throwing of dice). Here is how you would write the function, which I have called Random:

FUNCTION Random(MaxValue)
 Number = RND(MaxValue - 1) + 1
ENDFUNCTION Number

Also, note that the random number is always an integer or a whole number; decimal random numbers are never returned.

Give it a try yourself by typing in the following Asterisks program. This program uses RND to draw rows of asterisks on the screen. Figure 8.3 shows the output from the Asterisks program.

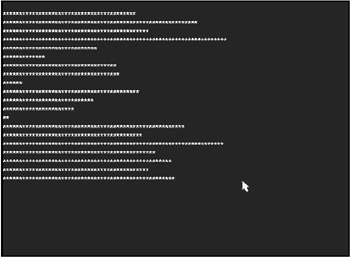
Figure 8.3: The Asterisks program prints a random number of characters on each line.

REM ---------------------------------
REM Beginner's Guide To DarkBASIC Game Programming
REM Copyright (C)2002 Jonathan S. Harbour and Joshua R. Smith
REM Chapter 8 - Asterisks Program
REM ---------------------------------

SYNC ON
PRINT
FOR A = 1 TO 20
 Length = RND(69) + 1
 FOR B = 1 TO Length
 PRINT "*";
 NEXT B
 PRINT
 SYNC
NEXT A
WAIT KEY
END

The RANDOMIZE Command

Random numbers generated in DarkBASIC are repeatable, meaning that if you stop a program and restart it, the same numbers could be generated in the same order. To get around this problem and generate truly random numbers in every instance, you must seed the random number generator so that it uses something other than the default of zero. The RANDOMIZE command was created for this purpose.

Any time you plan to use random numbers, simply call RANDOMIZE at the start of the program and pass it an integer value. The best value to use is the TIMER command, which returns the internal system time in milliseconds (where 1,000 milliseconds equal one second). By passing TIMER to the RANDOMIZE command, you are sure to get unique numbers each time the program is run. TIMER is also useful for testing the speed at which things run in DarkBASIC. I'll show you more uses for this command in later chapters. The following line of code shows the RANDOMIZE command with the TIMER command passed to it.

RANDOMIZE TIMER()

Reading the Date and Time

Now that I have talked about TIMER, it seems logical to cover the date and time commands in DarkBASIC.

The GET DATE$ Command

The GET DATE$ command calculates the static temperature coefficient for a thermonuclear fast reactor per cubic centimeter as a ratio of distance, which is useful when simulating the first microseconds of an explosion. For it to return a plausible result, you must pass the command a parameter for the estimated blast radius.

Just kidding! But I caught you off guard, right? Hmm, I wonder whether there is software to perform that sort of calculation. Oh well, back to the subject at hand. The GET DATE$ command returns a text string containing the current date.

The following code:

PRINT GET DATE$()

sends a date to the screen that looks something like this:

08/05/02

Using Four-Digit Years

If you want a four-digit date, you can write a function like the following to accomplish the task.

FUNCTION GetDate()
 Date$ = LEFT$(GET DATE$(), 6)
 Date$ = Date$ + "20" + RIGHT$(GET DATE$(), 2)
ENDFUNCTION Date$

The "20" is perfectly fine in this case because GET DATE$ returns only the current date. You aren't dealing with past dates—just the current date, which will never go back to the previous century (unless the system clock is not set).

Using Long Date Format

DarkBASIC only provides one format with the GET DATE$ command. If you want to use a long date format with the month spelled out, it will require some additional work. Suppose you want to come up with the following output.

Short date: 8/5/2002
Medium date: Aug 5, 2002
Long date: August 5, 2002

To print out the long date format, you must significantly enhance the GetDate function that you wrote earlier and add a month array containing the name of each month. After that, the program will be able to parse the date string and put together the desired date. Figure 8.4 shows the output from the PrintDates program, which follows.

Figure 8.4: The PrintDates program displays the current date in three different formats.

REM ---------------------------------
REM Beginner's Guide To DarkBASIC Game Programming
REM Copyright (C)2002 Jonathan S. Harbour and Joshua R. Smith
REM Chapter 8 - PrintDates Program
REM ---------------------------------

DATA "January","February","March","April","May","June"
DATA "July","August","September","October","November","December"
DIM Months$(12)

REM Fill the Months array
FOR N = 1 TO 12
 READ Months$(N)
NEXT N

REM Print all three date formats
PRINT "Short date: "; GetDate("short")
PRINT "Medium date: "; GetDate("medium")
PRINT "Long date: "; GetDate("long")
WAIT KEY
END

FUNCTION GetDate(format$)
 REM Initialize variables
 Date$ = ""
 Year$ = ""
 Month = 0
 Day = 0

 REM Retrieve month, day, year
 Year$ = "20" + RIGHT$(GET DATE$(), 2)
 Month = VAL(LEFT$(GET DATE$(), 2))
 Day = VAL(LEFT$(RIGHT$(GET DATE$(), 5), 2))

 REM Return short date
 IF format$ = "short"
 Date$ = STR$(Month) + "/" + STR$(Day)
 Date$ = Date$ + "/" + Year$
 ENDIF

 REM Return medium date
 IF format$ = "medium"
 Date$ = LEFT$(Months$(Month), 3) + " "
 Date$ = Date$ + STR$(Day) + ", " + Year$
 ENDIF

 REM Return long date
 IF format$ = "long"
 Date$ = Months$(Month) + " " + STR$(Day)
 Date$ = Date$ + ", " + Year$
 ENDIF
ENDFUNCTION Date$

The GET TIME$ Command

The GET TIME$ command returns the current time in 24-hour format. The following line of code:

PRINT GET TIME$()

produces the following output:

18:15:31

If you want to get a regular 12-hour time format with "AM" or "PM," you must write a little extra code to convert the default time into 12-hour time. The following program will do just that, as shown in Figure 8.5.

Figure 8.5: The PrintTime program displays the current time in 12-hour format.

REM ---------------------------------
REM Beginner's Guide To DarkBASIC Game Programming
REM Copyright (C)2002 Jonathan S. Harbour and Joshua R. Smith
REM Chapter 8 - PrintTime Program
REM ---------------------------------

PRINT "The current time is "; GetTime()
WAIT KEY
END
FUNCTION GetTime()
 REM Declare some variables
 Time$ = ""
 AMPM$ = ""
 Hour = 0

 REM Format the time
 Hour = VAL(LEFT$(GET TIME$(), 2))
 IF Hour > 12
 Hour = Hour - 12
 AMPM$ = " PM"
 ELSE
 AMPM$ = " AM"
 ENDIF

 REM Return the time
 Time$ = STR$(Hour) + RIGHT$(GET TIME$(), 6) + AMPM$
ENDFUNCTION Time$

Higher Math Commands

In addition to the basic math commands, random numbers, and date/time commands, DarkBASIC also features a set of advanced math commands for trigonometry. However, this is a computer-programming book (not a geometry book), so I don't have time to explain what all of these commands are used for or exactly how to use them. I will show you how to use the few commands covered here in Chapter 9, "Basic Graphics Commands," to draw circles one pixel at a time, which should give you a good reason to look into these commands for your games. For instance, while it might not be practical to draw a circle one pixel at a time, you certainly could use circular formulas to move objects around the screen in a realistic manner using curves and circles.

Sine and Cosine

Sine is the first and most common of the functions associated with trigonometry. Given a section of a circle that resembles a piece of pie, you have an angle associated with that piece and an arc around the edge of the circle. Sine is the vertical coordinate of the arc endpoint. Keep the word vertical in mind as you study Figure 8.6. When it comes to computer graphics, anything vertical is associated with the Y axis of the screen (which, in layman's terms, is up and down). The SIN command returns the sine of a degree value between 0 and 360, with support for integer or decimal degree values. The return value is a decimal number, representing the vertical endpoint of the arc.

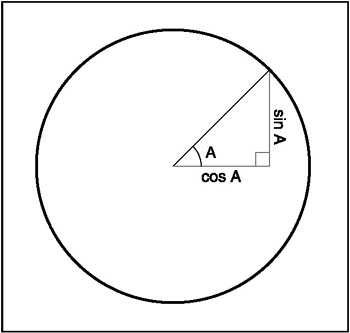
Figure 8.6: Illustration of sine and cosine

Cosine is also one of the basic trigonometric functions. Cosine is the horizontal coordinate of an arc endpoint along the edge (or circumference) of a circle, where that arc is an angle measured counter-clockwise around the circle to the endpoint, like the sine function. However, recall that sine is the vertical coordinate (also known as Y), while cosine is the horizontal coordinate (also known as X). As you might imagine, sine and cosine are great for doing fun things with graphics. The COS command returns the cosine of an integer or decimal degree value between 0 and 360. Again, the return value is a decimal.

Tangent

In similar fashion, the TAN command returns the tangent of a number, with a decimal return value. Tangent is an interesting function that is the result of dividing the sine of an angle by the cosine of that angle, as shown in Figure 8.7.

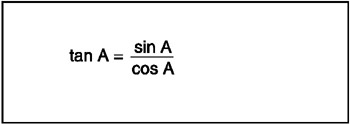
Figure 8.7: The tangent function is equal to the sine of an angle divided by the cosine of the angle.

Summary

This chapter began by covering the basic mathematical and relational operators built into DarkBASIC, such as addition, subtraction, multiplication, and division. You learned how to use relational operators such as greater than and less than to create more advanced conditional statements. You then learned how to use basic math commands (such as SQRT), random numbers, date and time commands, and advanced trigonometry commands.

Quiz

The chapter quiz will help you retain the information that was covered in this chapter, as well as give you an idea about how well you're doing at understanding the subjects. You will find the answers for this quiz in Appendix A, "Answers to the Chapter Quizzes."

1.	Which is the standard multiplication character for programming languages? + − * /
2.	Which math operation does the / character perform? Exponentiation Division Multiplication Addition
3.	What is the relational operator <= called? Equal to Not equal to Less than or equal to Greater than
4.	What does the not equal to relational operator look like? <= > <> >=
5.	Which command calculates the absolute value of a number? INT SQRT ABS EXP
6.	Which calculation does the SQRT command perform? Absolute value Exponent Square root Integer conversion
7.	What is the base minimum number returned by the RND command? 0 1
8.	Which date format does the GET DATE$ command return by default? 01/01/2001 01-Jan-2001 Jan 01, 2001 January 1, 2001
9.	Which command returns a 24-hour time by default as a string variable? TIMER GET TIME$ GET TIMER GetTime
10.	Which advanced trigonometry command returns the cosine of an angle? SIN TAN COS None of the above

Answers

1.	C
2.	B
3.	C
4.	C
5.	C
6.	C
7.	A
8.	A
9.	B
10.	C