2.1 Twisted Pair Cable
2.1.1 Specifications of Twisted Pair CableTwisted pair cables consist of copper wires of small diameters which are usually less than 0.1 inch for telephone, in-house, and office applications. Within a plastic covering shield, there are many individually insulated copper wires twisted with each other in pairs. Two wires in a tightly twisted pair experience almost the same physical environment. Therefore, radio emission and noise pickup are minimized when a differential signal is carried over the twisted pair. Furthermore, each twisted pair has its own twisting angle to minimize crosstalk between different pairs. The quality of the insulation material, the tightness and the precision of twists, and the diameter of the copper wire determine the transmission quality of a twisted pair cable. The size of the copper wire is usually measured in American Wire Gauge. Popular wire sizes for twisted pair cables are 19, 22, 24, and 26 AWG. Table 2.1 shows metric and English equivalences of AWG from 11 to 40. The English unit is mil, which is 0.001 inch, and the metric unit is millimeter. No AWG fits exactly an English or metric unit except AWG 36. However, the ratio between adjacent AWGs is about 0.890524585333. More than 100 years ago, wire gauges were set pretty much by how much you could reduce the diameter of the wire in one step through a wire drawing die. For a variety of reasons, each reduction is about the same ratio, leading to the geometric sequence we now have. Around the turn of the last century, the AWG group took the current gauge 10 and gauge 40 and interpolated accordingly. Similar earlier European wire gauge standards existed, but the current European definitions are metric based, and diameters of copper wire are specified to the accuracy of 0.1 mm. For example, the metric equivalents of 24 and 26 AWG twisted pair cables have diameters of 0.5 and 0.4 mm, respectively.
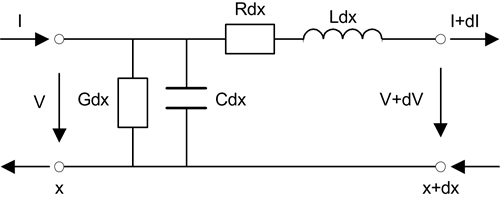
Twisted pair cables have been used for office wiring mainly to connect computers over 10BaseT or 100BaseTX Ethernet. Twisted pair cable types commonly used in office environments are Category 3 or Category 5. The transmission characteristics of Category 5 cable are better than those of Category 3 cable. There is also a Category 4 twisted pair cable with transmission qualities that fall between the two. Detailed cable-type recommendations as well as installation guidelines are in standards document TIA/EIA-568A [1], and TIA/EIA-568-B [2]. Transmission qualities of these twisted pair cables are generally defined by the attenuation at the frequency of 10 MHz. At that particular frequency, the attenuation should be less than 98, 72, or 65 decibels per kilometer (dB/km) for Category 3, 4, or 5 type of cable respectively. These cables can usually have 4 or 25 twisted pairs inside a plastic shield. Category 3 cable consists of 24 gauge copper wires, while Category 4 and Category 5 cables can be made with either 22 or 24 gauge wires. Again, the transmission quality of a twisted cable is not just dependent on the inside copper wire size. There are no official standards for residential wiring practice. before the divestiture of the Bell system, wiring practice was very much phone company and region-dependent. These practices have been followed by regional phone company technicians and building contractor electricians thereafter. A study [3] has found most in-premises telephone wirings are either Quad or flat type. A Quad cable has four wires all twisted together without individual pairing. A flat cable has 4 wires lying next to each other in one layer without any twisting. There are also three or six pair cables either all twisted together or lying flat. The Quad cable usually consists of 22 AWG copper wires, while the flat cable is usually made with 26 AWG copper wires. Since transmission qualities of twisted pair cables vary depending on wire size as well as other manufacturing processes, the performance of a particular twisted pair cable can be accurately defined only by its primary electric parameters in terms of resistance, inductance, capacitance, and conductance per unit length. Such a definition is not considered as a manufacturing standard but rather as an industry reference model. Twisted pair cable models defined by their primary electric parameters have been very useful in computer simulation studies leading to definitions of advanced broadband communication systems such as DSL and Ethernet. Electric parameters of a particular twisted pair cable might be a little different from those of the reference model owing to temperature, measuring procedure, and manufacturers. However, the general transmission performance of the reference model can be maintained if differences are kept minimal. 2.1.2 Primary Parameters of Twisted Pair CablesThe transmission characteristics of a twisted pair cable can be accurately defined by its primary electric parameters, namely the series resistance R, series inductance L, shunt conductance G, and shunt capacitance C. Note that these primary parameters are also frequency-dependent. Values of these primary parameters are expressed per unit length. Therefore, the values should be properly scaled for either metric or English measuring system. Figure 2.1 shows a twisted pair cable equivalent circuit in terms of its primary parameters for a unit length dx. The equivalent circuit of a twisted pair cable should consist of many such unit length circuits connected in cascade. Figure 2.1. Twisted Pair Distributed Parameter Model
Primary parameters of a twisted pair cable can be measured directly or indirectly with wide bandwidth and high-precision test equipment. However, data fitting is necessary to cover the whole frequency band and to filter out some inaccurate spots. Parameterized models [4] for RLGC primary parameters have been developed to fit the measured values. Parameter models are Equation 2.1
where r0C is the copper DC resistance and r0S is steel DC resistance, while aC and aS are constants characterizing the rise of resistance with frequency in the "skin effect" for the series resistance Equation 2.2
where l0 and l Equation 2.3
where c Equation 2.4
where g0 and ge are constants chosen to fit the measurements for the shunt conductance. r0s is presented to take care of the double skin-effect of some copper-clad drop wires with steel cores, and its value is normally Equation 2.5
Table 2.2 shows parameterized models, parameters in Equations 2.2 to 2.5, for typical office and residential twisted pair cables.
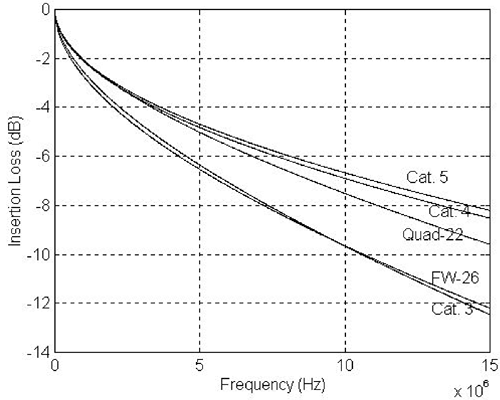
These parameterized models can be used to generate twisted pair primary electric parameters for frequencies from near 0 up to 50 MHz with reliable accuracy compared with real measurements. 26 AWG and 24 AWG types are commonly used in telephone loops, while Drop Wire and Flat Pair are often used to connect telephone loops to subscriber households. The Category 5 twisted pair is popular for Ethernet wiring. Quad-22, consisting of four 22 AWG twisted pairs, and FW-26, 26 AWG of flat wire, are regularly found in in-house telephone wiring. A set of secondary parameters for the twisted pair cable consists of characteristic impedance and propagation constants. The characteristic impedance of a twisted pair cable is related to primary parameters according to the following expression: Equation 2.6
The propagation constant of a twisted pair cable is also related to primary parameters and can be expressed according to the following expression: Equation 2.7
Note that the characteristic impedance and propagation constants of a twisted pair cable are also frequency-dependent. Although the propagation constant is a function of frequency, we still use the name "propagation constant" following its original derivation from an ideal transmission line. For a simple twisted pair cable terminated with its characteristic impedance, its transfer function or insertion loss is related to the propagation constant according to the following expression: Equation 2.8
where d is the length of the twisted pair cable. The measurement of the transfer function or the insertion loss of a twisted pair cable is relatively straightforward, and the measurement result is often expressed in terms of the output-to-input power ratio. Specifically, a scaled version of the logarithm of the output-to-input power ratio is used to describe the transfer function of a twisted pair cable. The logarithmic version of transfer function is defined by the following expression: Equation 2.9
where a(f) is the real part of propagation constant g(f) . a(f) can be approximately represented in the following expression: Equation 2.10
Parameters of a and b for insertion loss are listed in Table 2.3 for different twisted pair cables and in-house wirings [5]. These parameters should be used in conjunction with distance d in terms of feet (ft) and frequency f in terms of Hertz (Hz).
Figure 2.2 shows insertion losses created according to these estimated propagation constant model parameters for a distance of 100 m or 328.08 ft. Figure 2.2. Insertion Loss According to Propagation Parameter Estimations
|
EAN: 2147483647
Pages: 97
- Assessing Business-IT Alignment Maturity
- Linking the IT Balanced Scorecard to the Business Objectives at a Major Canadian Financial Group
- Technical Issues Related to IT Governance Tactics: Product Metrics, Measurements and Process Control
- Governance in IT Outsourcing Partnerships
- The Evolution of IT Governance at NB Power
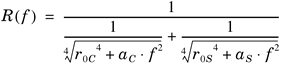
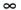 are the low-frequency and high-frequency inductances, respectively, and
are the low-frequency and high-frequency inductances, respectively, and  /km)
/km)