| As mentioned, this chapter covers many of the same topics as Chapter 12, "Engines," although a few differences arise when you implement a language. For example, the engine accepts any object as a functor, whereas Logikus allows only lowercase strings, quoted strings, or numbers . The engine accepts any string as the name of a variable, whereas Logikus variable names must begin with a capital letter and may not contain whitespace. Because of these subtle differences, an explanation of Logikus is a somewhat different discussion than an explanation of the engine. However, on the topic of proofs, Logikus behaves exactly as the engine does. As a result, this section covers the same information as Section 12.7, "Proofs." If you have read that section, you can skip ahead here to Section 13.7.4, "Looping and Halting." 13.7.1 Variable Scope Structures generally prove themselves by unifying with an axiom in a program and then proving that axiom 's tail, if any. The behavior of structures in the tail of a rule or in a query depends on the fact that variables in a query or rule share the same scope. A variable's scope is the rule or query in which it appears. Another variable with the same name in another rule is a different variable. For example, a program might contain the following two rules: highCity(Name) :- city(Name, Alt), >(Alt, 5000); largeCountry(Name) :- country(Name, Pop), >(Pop, 10000000); The Name variable in the first rule is the same variable throughout that rule, and it is completely independent of the Name variable in the second rule. In a query, a variable's scope is the query. So, for example, the query city(X, X) cannot match city(denver, 5280) because X can take on only one of the two values: denver or 5280 . 13.7.2 Variable Joins The fact that all the variables in a rule have the same scope allows the construction of relational joins. A relational join connects two facts according to a common element. For example, consider a collection of facts about coffee types, customers, and their orders from a coffee company: coffee("Launch Mi", french, kenya, 6.95); coffee("Simple Best", regular, colombia, 5.95); coffee("Revit", italian, guatemala, 7.95); coffee("Brimful", regular, kenya, 6.95); coffee("Smackin", french, colombia, 7.95); customer("Jim Johnson", 2024); customer("Jane Jerrod", 2077); customer("Jasmine Jones", 2093); order(2024, "Simple Best", 1); order(2077, "Launch Mi", 3); order(2077, "Smackin", 3); order(2093, "Brimful", 2); In this data, a coffee structure contains the name of a type of coffee, the roast, the country of origin, and the price per pound . The customer facts include the name of the customer and the customer number. The order facts record a standing order that the company ships monthly. They show the customer number, the type of coffee, and the number of pounds to ship each month. As Figure 13.3 shows, to see the types of coffee each customer has ordered, you can use the query customer(Name, Cnum), order(Cnum, Type, Pounds) Figure 13.3. A join. All the variables in a query are in the same scope, so this query joins customer and order facts on customer number. 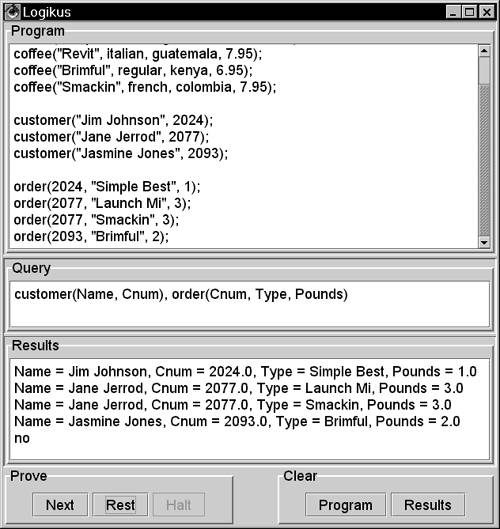 Queries and rules prove themselves in the same way: by proving each of their structures in turn . Each structure may find multiple successful proofs of itself, and each structure unifies its variables with each proof. For example, the query customer(Name, Cnum), order(Cnum, Type, Pounds) proves itself by proving customer and then order . When this rule proves itself, it first asks customer to prove itself. The customer structure looks through the program and unifies with the fact customer("Jim Johnson", 2024) The structure proves itself by unifying with a fact in the program. This structure succeeds, and so the rule asks its next structure to prove itself. This structure shares variables with the first structure; all the structures in a rule have a common scope. So this structure must effectively prove order(2024, Type, Pounds) The customer number is fixed at this point. This screens out all possible proofs except one. The structure proves itself by unifying with the fact order(2024, "Simple Best", 1) By unifying with this fact, the order structure of the query succeeds. Because this is the last structure in the query, the entire query succeeds, with its variables unified with values that make the query true. After a successful proof, the IDE prints the query's variables. 13.7.3 Backtracking In Figure 13.3, the user has pressed the Rest button. After its first success, the IDE asks the query to prove itself again. The query does not begin its proof anew. To find another proof, the query asks its last structure to find another proof. In this case, there is no other order fact with customer number 2024 , and the last structure in the query fails to find another proof. The query then backtracks, which means that the query asks the preceding structure to find a new proof. In this example, the preceding structure is customer . When a structure looks for a new proof, it first unbinds any variables it bound in its previous proof. In this example, the customer structure is able to find a new proof, unifying with the fact customer("Jane Jerrod", 2077) This proof unifies the query's variables with new values, and that produces new chances for the latter structures to prove themselves. The query moves forward again and asks its order structure to prove itself. This amounts to proving order(2077, Type, Pounds) There are two possible proofs because there are two orders for customer number 2077 . The structure first unifies with the fact order(2077, "Launch Mi", 3) This unification completes a second successful proof of the query, and the IDE prints the new values of the variables. The IDE then asks the query for another proof. The query searches for a new proof by asking its last structure whether it can find another proof. In this case it can. First, the structure unbinds the variables it bound in finding its last proof. Specifically, the order structure unbinds the variables Type and Pounds . The structure unbinds only the variables it bound; it does not unbind Cnum because an earlier structure bound that variable. With its Cnum variable still unified with 2077 , the order structure finds another fact to unify with: order(2077, "Smackin", 3) This results in a new proof, and the IDE prints the result. The IDE keeps asking for more proofs. The query fails to find another proof for order 2077 , and the query backtracks to the customer structure. This structure unbinds its variables and unifies with the fact customer("Jasmine Jones", 2093) The order structure then unifies with order(2093, "Brimful", 2) This constitutes the last successful proof. When the IDE asks for yet another proof, the query tries to find another order for customer number 2093 . When this fails, the query tries to find another customer with which to unify. There are none, so the first structure of the query fails, the entire query fails, and the IDE prints no . 13.7.4 Looping and Halting Logikus rules can refer to other rules, including themselves. This capability lets you construct powerful, recursive algorithms. In addition, this ability lets you create loops , which may compute until your program runs out of available memory. To help handle this prospect, the Logikus IDE provides a Halt button. The IDE executes Logikus proofs in a separate thread, which you can stop if you think the proof will not complete. For example, consider a program that contains the rule loop :- loop; This rule says, "to prove loop , prove loop ." If this rule executes, it will loop forever, or until your program runs out of memory. Try entering this rule in a Logikus program and issuing the query "loop" . While the query futilely pursues its proof, you can click the Halt button to stop it. However, if your program runs out of memory resources, this button may not be able to execute. 13.7.5 Gateways Compared with other structures, comparisons behave differently in proofs. First, their truth or falsity depends on their terms, so they need not consult a program. Second, a comparison can be true no more than once. After a comparison participates in a successful proof, it does not search for alternative proofs. For example, consider the query coffee(Name, Roast, Country, Price), >(Price, 6), order(Cnum, Name, Pounds); In this query, the comparison on price acts as a gateway, which is a structure that can be true no more than once. When the coffee structure unifies with a fact in a program, the Price variable unifies with the coffee price. At this point, the price is either greater than 6 or it is not. Unlike the coffee and order structures, the comparison structure can be true no more than once. If the comparison is true, the query moves on and finds proofs of the order structure. When the order structure runs out of proofs, the rule backtracks to the comparison and asks for another proof, and the comparison returns false; there is no other way to prove that the comparison is true. You'll meet two other gateways ”evaluations and negations ”when we look into additional features of Logikus. |

