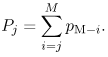| In this section it is assumed that there are 120 machines in the data center and that the MTTF is equal to 500 minutes (i.e., l = 1/500 = 0.002 failures per minute). The average time taken by a repair person to diagnose and repair a machine is assumed, unless stated otherwise, to be equal to 20 minutes (i.e., m = 1/20 = 0.05 repairs per minute). The questions of Section 7.2 are now revisited and answered below. Given the rate at which machines fail, the number of machines, the number of repair people, and the average time it takes to repair a machine, what is the probability that exacly j (j = 1, ···, M) machines are operational at any given time? The probability that j machines are operational at any given time is the probability that M j machines are failed. This probability, pM j, is computed using Eqs. (7.3.4) and (7.3.5). Figure 7.3 shows this probability for three different values of the number of repair people (N = 2, 5, and 10). If only two repair people are used, the peak of the distribution occurs for about 50 machines and the probability that 50 machines are operational is about 5.6%. For N = 2, the probability that j machines are operational is negligible for j  67. When five repair people are used, the situation improves dramatically. The peak of the distribution occurs for 116 machines. At that point, the probability that exactly 116 machines are operational is close to 10%. The bulk of the distribution is concentrated between 92 and 120 machines. Adding five more people to the repair staff (i.e., Figure 7.3. Probability that exactly j machines are operational vs. j for M = 120, l = 0.002 and m = 0.05. 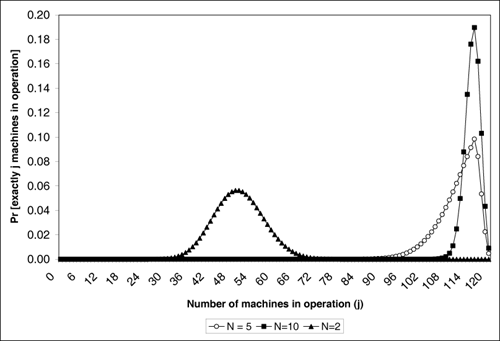 Given the failure rate l, the number of machines M, the number of repair people N, and the average repair time 1/m, what is the probability Pj that at least j machines are operational at any given time? The probability Pj that at least j machines are operational can be computed as Equation 7.4.10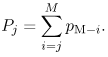 
Equations (7.3.4)-(7.3.5) provide the values of the probabilities pM i required in Eq. (7.4.10). The values of Pj are shown in Fig. 7.4 for j = 1, ···, 120 and for N = 2, 3, 4, 5, and 10. As expected, for low values of j the probability of j machines being operational is very close to 1. It is interesting to note the dramatic drop in each curve. This indicates that once the service personnel become overloaded, the entire system (i.e., nearly all the machines) tends toward failure. Having extra machines, beyond the number that the service personnel can maintain is pointless. Figure 7.4. Probability that at least j machines are operational vs. j for M = 120, l = 0.002 and m = 0.05. 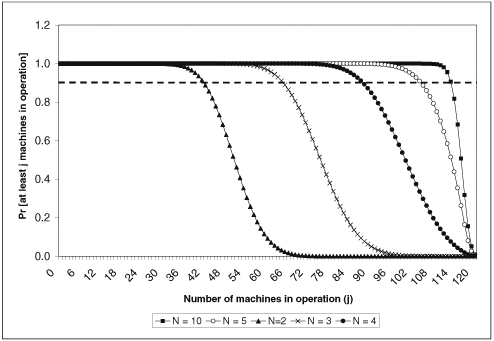 For example, for N = 2, the probability that at least 40 machines are operational is 0.935 and the probability that at least 50 machines are operational is 0.52. The probability that at least 70 machines are in operation is virtually zero for N = 2. If the desired service level agreement is to have 110 machines operational, this SLA could not be met with a service staff size of 2 or 3. The SLA would only be met 14% of the time with a staff size of 4, 70% of the time with a staff size of 5, and 99% of the time with a staff size of 10. Given the failure rate l, the number of machines M, and the average repair time 1/m, how many repair people are necessary to guarantee that at least two thirds of the machines (i.e., j = 80) are operational with a probability Pj = 0.9? Figure 7.4 shows that the horizontal dashed line for Pj = 0.9 intersects the N = 4 curve for j = 88 machines and the N = 3 curve for j = 64 machines. This indicates that at least four repair people are needed. Less than four would not guarantee that 80 machines are up and running with a probability of 0.9. A staff of four would guarantee that up to 88 machines are operational with a 0.9 probability. What is the effect of the size of the repair team, N, on the mean time to repair (MTTR) a machine? Also, what is the effect of N on the percentage of machines that can be expected to be operational at any given time? Using various values of N, the probabilities pk are computed and the aggregate failure rate 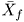 is found according to Eq. (7.3.6). Then, the MTTR is obtained using Eq. (7.3.7). The results are shown in Table 7.1. The table shows a sharp decrease in MTTR as N varies from 1 to 5. As the number of repair people is increased beyond 5, further decreases in the MTTR are minimal. With 5 repair people, the average time a machine is in failure mode (i.e., MTTR) is 38 minutes (i.e., 18 minutes waiting to be serviced and 20 minutes of service time). Also, with 5 repair people, an average of 111 (i.e., 93%) of the machines can be expected to be operational at any given time. Table 7.1. Effect of Number of Repair PeopleN | No | Nf | MTTR (min) | (No/M) x 100 (%) |
|---|
1 | 25.0 | 95.0 | 1900.0 | 20.8 | 2 | 50.0 | 70.0 | 700.0 | 41.7 | 3 | 75.0 | 45.0 | 300.0 | 62.5 | 4 | 99.2 | 20.8 | 104.8 | 82.7 | 5 | 111.5 | 8.5 | 38.1 | 92.9 | 6 | 114.3 | 5.7 | 25.1 | 95.2 | 7 | 115.0 | 5.0 | 21.7 | 95.8 | 8 | 115.3 | 4.7 | 20.6 | 96.0 | 9 | 115.3 | 4.7 | 20.2 | 96.1 | 10 | 115.4 | 4.6 | 20.1 | 96.1 | 120 | 115.4 | 4.6 | 20.0 | 96.2 |
The last line of Table 7.1 shows the case in which N = M = 120 (i.e., where each machine has its own personal repair person). This is a degenerate case, but is helpful in illustrating the best possible performance for the system. In this case, machines never wait to be serviced. Thus, MTTR = 1/m. Applying Little's Law to the cycle composed of machines in operation and machines being repaired yields Equation 7.4.11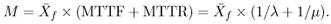 
Thus, Equation 7.4.12 
Applying Eq. (7.3.9) to find the average number of machines in operation, No, yields Equation 7.4.13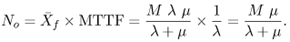 
Substituting the values of M = 120, l = 0.002 failures/min, and m = 0.05 repairs/min into Eq. (7.4.13) yields a value of No = 115.4 (= (120 x 0.05)/(0.002 + 0.05)). This indicates that the upper limit on the number of machines that can be expected to be operational at any given time is 115.4. This assumes that each machine has its own repair person. However, as noted above, a repair staff size of 5 is expected to keep 111 machines operational. With an expected down time of 38 minutes per failed machine, this appears to be a prudent design decision. What is the effect of a repair person's skill level (i.e., the average time 1/m required to fix a machine) on the overall down time (i.e., MTTR)? Also, how does the skill level affect the percentage of operational machines? Assuming, N = 5, the value of m is varied so that the average time taken by a repair person to fix a machine varies from 10 min (i.e., m = 1/10 = 0.10) to 25 min (i.e., m = 1/25 = 0.04). The results are shown in Table 7.2. As expected, more skilled and faster repair people can improve the availability of the machines for the same number of people N and the same failure rate l. For example, if N = 5 and each repair person is able to diagnose and fix a machine in 10 minutes on average, then the average down time is 10.4 min and 118 (i.e., 98%) of the machines remain operational. If N = 5 and if it takes an average of 25 minutes to repair a machine, Table 7.2 indicates that the average down time is 105 minutes and only 99 (i.e., 83%) of the machines are operational. From Table 7.1, this same level of performance can be achieved with N = 4, but with an average repair time of 20 minutes.
Table 7.2. Effect of the Repair Rate mAvg. time to repair a machine (min) | Repair Rate (m) (1/min) | No | Nf | MTTR (min) | (No/M) x 100 (%) |
|---|
10 | 0.100 | 117.6 | 2.4 | 10.4 | 98.0 | 12 | 0.083 | 117.0 | 3.0 | 12.9 | 97.5 | 15 | 0.067 | 115.8 | 4.2 | 18.1 | 96.5 | 18 | 0.056 | 113.8 | 6.2 | 27.2 | 94.8 | 20 | 0.050 | 111.5 | 8.5 | 38.1 | 92.9 | 25 | 0.040 | 99.1 | 20.9 | 105.5 | 82.6 |
|
