14.6 Flow-Equivalent Server Method

Divide and conquer is a common approach to solving problems in computing. It also applies to solving queuing models. According to this principle, it is often efficient to solve a queuing network by partitioning it into several smaller subnetworks and then combining the solutions of the subnetworks into an approximate solution for the entire network. This approach is referred as decomposition and aggregation. The basic idea is to replace each subnetwork of queues by a single load-dependent queue, which is flow-equivalent to the subnetwork.

The inspiration for the flow equivalent server (FES) method stems from Norton's Theorem for electrical circuits [5]. For repeated evaluations, the solution of a flow-equivalent server model requires less computation than the original one. This technique is useful in modeling large systems because it allows large queuing networks to be decomposed and reduced to a series of smaller queuing models.

Consider a closed queuing network model composed of a number of queues and a total population size of N. The FES algorithm consists of the following sequence of steps [3, 5, 12].

• Select a queue or a set of queues, that form the subnetwork b, that will be analyzed in detail.
  
  
• Construct a reduced network by replacing subnetwork b by a "short" (i.e., set the service time of all the servers of the subnetwork b to zero).
  
  
• Solve the reduced network using the MVA algorithm. Determine the throughput of the reduced network when there are n customers in the network, n = 0,1,2,...N.
  
  
• Replace the reduced network by a load-dependent "Flow Equivalent Server (FES)" whose load-dependent service rate, m(n), is equal to the throughput of the shorted network with n customers, n = 0,1,2,...N.
  
  
• The network formed by subnetwork b and the FES is equivalent to the original network. The behavior of subnetwork b in the equivalent network is the same as in the original network. The equivalent network is solved using MVA techniques with load-dependent servers.
  
  

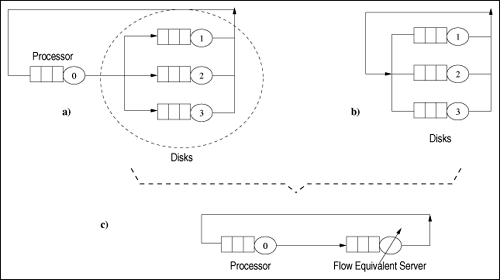
When the flow-equivalent method is applied to closed single-class product-form models, it yields exact results [3]. In non-product form cases, some error is introduced. Courtois [6] has shown that relatively small errors are introduced with this approximation if the rate at which transitions occur within the subnetwork is much greater than the rate at which the subnetwork interacts with the rest of the network (i.e., the reduced FES network).

Example 14.6.

Consider the queuing network model of Fig. 14.11(a), representing a server, disks, and with multiple custmomer threads. The system is composed of one processor and three disks. When a thread is executing and issues an I/O request it gets blocked until the request is satisfied. Assume that the server operates with three threads. The model parameters are: S₀ = 2/15 sec, V₀ = 3, D₀ = 0.4 sec, S₁ = S₂ = S₃ = 1 sec, V₁ = V₂ = V₃ = 1, D₁ = D₂ = D₃ = 1 sec, and n = 3. The purpose of this example is to analyze the queuing model using the FES method. The original network is shown in Fig. 14.11(a). The subnetwork b in this example consists of the processor. Step 2 sets the processor time to zero and creates a reduced network composed of three disks as indicated in Fig. 14.11(b) (i.e., the disk subsystem). This reduced network is solved for each thread population value (n = 1,2,3). The MVA algorithm calculates the throughput of the disk subsystem: X(1) = 0.333 requests/sec, X(2) = 0.5 requests/sec, and X(3) = 0.6 requests/sec. The disk subnetwork is then replaced by a load-dependent FES with the mean service rates equal to X(1), X(2), X(3). The original system is then reduced to a network composed of the processor and the load-dependent FES server, as illustrated in Fig. 14.11(c). Since the original model has a product-form solution, the results calculated for the flow-equivalent model exactly match those of the original model. By using the load-independent MVA algorithm om the model of Fig. 14.11(a) and the load-dependent MVA algorithm on the model of Fig. 14.11(c), the same results for throughput and response time, namely 0.569 threads/sec and 5.276 sec, respectively, are obtained.

Figure 14.11. Flow-equivalent technique.