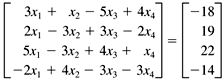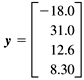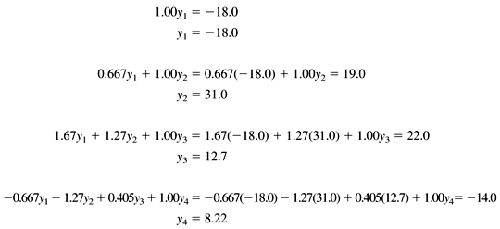10.5 LU Decomposition

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  10.   Solving Systems of Linear Equations

---

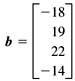
10.5 LU Decomposition

Now let's see how we can implement the Gaussian elimination algorithm using matrices. Our original system of linear equations will serve as an example.

If we collect the coefficients of the system into a square matrix A, put the values after the equal signs on the right-hand side into a column vector b, and represent the unknowns x _i as the column vector x, then we have the matrix equation Ax = b. For example, our system of linear equations becomes

If we do the matrix multiplication, we get

which is equivalent to the original system.

After we're done with forward elimination, we'll have an upper triangular matrix U. For our system of equations, U is

The forward elimination process produces an upper triangular matrix by subtracting multiples of the pivot row from each row below the pivot row. So, to recover the original matrix A from U, we want to add those multiples of the pivot row. We can do that with a lower triangular matrix L that contains ones on the diagonal and the multiples below the diagonal. For our system of equations,

We can verify that, indeed (subject to roundoff errors), LU = A. The process of decomposing (factoring) matrix A into matrices L and U is called LU decomposition.

When we did the forward elimination by hand, the right-hand-side values participated in the process. From the matrix point of view, we started with the column vector

and ended up with a new column vector, which we'll call y:

We then performed back substitution with these values to compute the values of the solution vector x.

We began with the equation Ax = b, and by performing forward elimination, we transformed the equation to Ux = y:

which we can solve for x using back substitution.

If we think about it, having the right-hand-side values participate in the forward elimination process really isn't such a good idea. Here's why. Suppose then we're given a new set of right-hand-side values b ', and we're asked to solve for x using these new values. We'd have to go through the forward elimination process again to compute the corresponding y '. We'd also end up with the same U, and so we would redo work we'd already done.

So, given a vector b, we want a quick way to compute the corresponding vector y without repeating work. But just as we have LU = A, we also have Ly = b:

Do the matrix multiplication and use a process similar to back substitution called forward substitution, which solves the y _i from the top down:

Roundoff errors from using only three significant digits account for the discrepancies between these values and the ones we saw above in the equation Ux = y.

Then we go back to the equation Ux = y and solve for x using back substitution.

Adding scaling and partial pivoting to these matrix operations is straightforward. Scaling is multiplying the elements of a row of matrix A by a nonzero value, and partial pivoting involves exchanging rows of the matrix.

---

Top