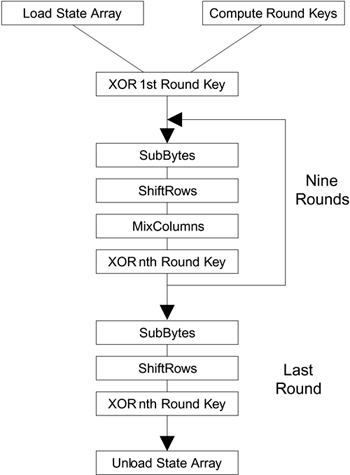
Steps in the AES Encryption Process
| The encryption process uses a set of specially derived keys called round keys. These are applied, along with other operations, on an array of data that holds exactly one block of data the data to be encrypted. This array we call the state array. You take the following steps to encrypt a 128-bit block:
The reason that the rounds have been listed as "nine followed by a final tenth round" is because the tenth round involves a slightly different manipulation from the others. The block to be encrypted is just a sequence of 128 bits. AES works with byte quantities so we first convert the 128 bits into 16 bytes. We say "convert," but, in reality, it is almost certainly stored this way already. Operations in RSN/AES are performed on a two-dimensional byte array of four rows and four columns. At the start of the encryption, the 16 bytes of data, numbered D0 D15, are loaded into the array as shown in Table A.5. Each round of the encryption process requires a series of steps to alter the state array. These steps involve four types of operations called:
The details of these operations are described shortly, but first we need to look in more detail at the generation of the Round Keys, so called because there is a different one for each round in the process. Round KeysThe cipher key used for encryption is 128 bits long. Where this key comes from is not important here; refer to Chapter 10 on key hierarchy and how the temporal encryption keys are produced. The cipher key is already the result of many hashing and cryptographic transformations and, by the time it arrives at the AES block encryption, it is far removed from the secret master key held by the authentication server. Now, finally, it is used to generate a set of eleven 128-bit round keys that will be combined with the data during encryption. Although there are ten rounds, eleven keys are needed because one extra key is added to the initial state array before the rounds start. The best way to view these keys is an array of eleven 16-byte values, each made up of four 32-bit words, as shown in Table A.6. To start with, the first round key Rkey0 is simply initialized to the value of the cipher key (that is the secret key delivered through the key hierarchy). Each of the remaining ten keys is derived from this as follows.
For each of the round keys Rkey1 to Rkey10, words W1, W2, W3 are computed as the sum[1] of the corresponding word in the previous round key and the preceding word in the current round key. For example, using XOR for addition:
The rule for the value of W0 is a little more complicated to describe, although still simple to compute. For each round key Rkey1 to Rkey10, the value of W0 is the sum of three 32-bit values:
Thus, we write:
where W >>> 8 means rotate right 8 for example (in hexadecimal) 1234 becomes 4123 and Rcon[i] is an entry in Table A.7.
There is a good reason why the sequence of this table suddenly breaks off from 128 to 27. It is because of the way finite fields overflow, as described in the previous section. Although the algorithm for deriving the round keys seems rather complicated, you will notice that no difficult computations have been performed and it is not at all computationally intensive. Also note that, after the first, each key is generated sequentially and based on the previous one. This means that it is possible to generate each round key just in time before it is needed in the encryption computation. Alternatively, if there is plenty of memory, they can be derived once at the start and stored for use with each subsequent AES block. Computing the RoundsHaving described how the round keys are derived, we can now return to the operations used in computing each round. Earlier we mentioned that four operations are required called:
Each one of these operations is applied to the current state array and produces a new version of the state array. In all but the rarest cases, the state array is changed by the operation. The details of each operation are given shortly. In the first nine rounds of the process, the four operations are performed in the order listed. In the last (tenth) round, the MixColumns operation is not performed and only the SubBytes, ShiftRows, and XorRoundKey operations are done. SubBytesThis operation is a simple substitution that converts every byte into a different value. AES defines a table of 256 values for the substitution. You work through the 16 bytes of the state array, use each byte as an index into the 256-byte substitution table, and replace the byte with the value from the substitution table. Because all possible 256 byte values are present in the table, you end up with a totally new result in the state array, which can be restored to its original contents using an inverse substitution table. The contents of the substitution table are not arbitrary; the entries are computed using a mathematical formula but most implementations will simply have the substitution table stored in memory as part of the design. ShiftRowsAs the name suggests, ShiftRows operates on each row of the state array. Each row is rotated to the right by a certain number of bytes as follows:
As an example, if the ShiftRows operation is applied to the stating state array shown in Table A.8, the result is shown in Table A.9. MixColumnsThis operation is the most difficult, both to explain and perform. Each column of the state array is processed separately to produce a new column. The new column replaces the old one. The processing involves a matrix multiplication. If you are not familiar with matrix arithmetic, don't get to concerned it is really just a convenient notation for showing operations on tables and arrays. The MixColumns operation takes each column of the state array C0 to C3 and replaces it with a new column computed by the matrix multiplication shown in Figure A.2. Figure A.2. MixColumns Operation
The new column is computed as follows:
Remember that we are not using normal arithmetic we are using finite field arithmetic, which has special rules and both the multiplications and additions can be implemented using XOR. XorRoundKeyAfter the MixColumns operation, the XorRoundKey is very simple indeed and hardly needs its own name. This operation simply takes the existing state array, XORs the value of the appropriate round key, and replaces the state array with the result. It is done once before the rounds start and then once per round, using each of the round keys in turn. DecryptionAs you might expect, decryption involves reversing all the steps taken in encryption using inverse functions:
XorRoundKey doesn't need an inverse function because XORing twice takes you back to the original value. InvSubBytes works the same way as SubBytes but uses a different table that returns the original value. InvShiftRows involves rotating left instead of right and InvMixColumns uses a different constant matrix to multiply the columns. The order of operation in decryption is:
The same round keys are used in the same order. Summary of AESNow we have seen all the steps needed to take a 128-bit block of data and transform it into ciphertext. We also looked at the reverse process for decryption. The process of encryption can be summarized as shown in Figure A.3. The mathematics behind the algorithm is rather hard to understand for nonmathematicians and we have focused on how rather than why in this book. If you are interested in such matters, it is probably worth reading the theoretical papers of looking at the book that specialize in cryptography. What is interesting, however, is the way in which all the operations are based on byte values and operations that are simple to implement in digital logic gates. AES achieves the goal of being both secure and practical for real systems. Figure A.3. Summary of AES/RSN Encryption
|
EAN: 2147483647
Pages: 151
- ERP Systems Impact on Organizations
- Enterprise Application Integration: New Solutions for a Solved Problem or a Challenging Research Field?
- Distributed Data Warehouse for Geo-spatial Services
- A Hybrid Clustering Technique to Improve Patient Data Quality
- Development of Interactive Web Sites to Enhance Police/Community Relations