Sound and Perception
Sound isn't just a phenomenon in physics: what happens inside your ear and brain is equally important. Psychoacoustics is the study of the subjective perception of sound, sound as we experience it on a daily basis as vibrations reach our ear and are relayed to the brain. Ultimately, of course, it's the human listener we care about in digital audio and music, so it's vital to understand how frequency and amplitude translate into perceived pitch, loudness, and timbre.
How We Hear Musical Pitch
If you have any musical training, you probably think about pitch in terms of musical note names , not Hertz. Although the way we hear pitch is based in part on the physical reality of sound, it's also learned through musical experience. We train our ears to hear sound in relation to tuned musical pitches. So what's going on when we hear an audio frequency and perceive it as a certain musical pitch?
Audible range
To be heard by human ears at all, sound needs to be in the audible frequency range. You could feel a 1 Hz oscillation if the amplitude were great enough, but you couldn't hear it. (It's still sound; it's just sound below the range of what you can hear.)
Sound is only audible if it lies between about 20 Hz and about 22,000 Hz. Frequencies below that range are called infrasonic or subsonic ; above are called ultrasonic . Subsonic frequencies are sometimes used in audio to modulate other sounds. If a sound contains both partials within the audible frequency range and ultrasonic partials, we'll hear only the partials within the audible range.
At around 20 oscillations each second, or 20 Hz, most healthy adults can begin to hear a sound. The bottom note of the piano (A0) is just below 28 Hz. The A above middle C (A4), 440 Hz, is the note to which most orchestras and other ensembles tune. (This is the first note you hear before an orchestra begins tuning, as played by the oboe.) The top note of a piano is less than 4,200 Hz, but you can hear much higher, up to about 22,000 Hz for a healthy young adult.
Key tone
It's fairly easy to understand how our ears can discern pitch from a single sine wave: the number of compressions and rarefactions in a span of time translate directly to frequency. But your ears can also perceive a dominant pitch in more complex sounds that are rich in partials, sounds that contain energy at many different frequencies. When you hear an instrument play a note and hear the note G, you're not just hearing sound with the frequency that corresponds to G. Your ear detects the sound of one partial as the most significant, the key tone . Usually, as with a piano or violin, it's the lowest partial or fundamental, although in rare cases (as with more clangorous sounds like a church bell) the key tone may be one of the overtones. Regardless, your ear identifies that pitch as the important one while hearing the other partials as contributing to the color of the sound. Without this capability, we wouldn't be able to hear a melody.
High, low, and octaves
If you can hum a tune (even badly ), you can perceive "high" and "low" frequencies as they relate to one another. That is, you can probably pick out basic contours and recognize one melody from another by identifying which pitches sound higher or lower in relation to one anotherat least near the center of the frequency spectrum, where musical pitches occur.
On a basic level, this perception of high and low corresponds to frequency: faster frequencies sound higher in pitch, and slower frequencies sound lower in pitch. The way we hear the ratio of one pitch to another, however, is more complex. We hear sound in musical space along a geometric curve rather than a straight line: that is, if we hear two different frequencies (a musical interval) and compare them to one another mentally, the same difference in frequency in Hz will sound like a bigger change in relative pitch if the frequencies are lower than if the frequencies are higher.
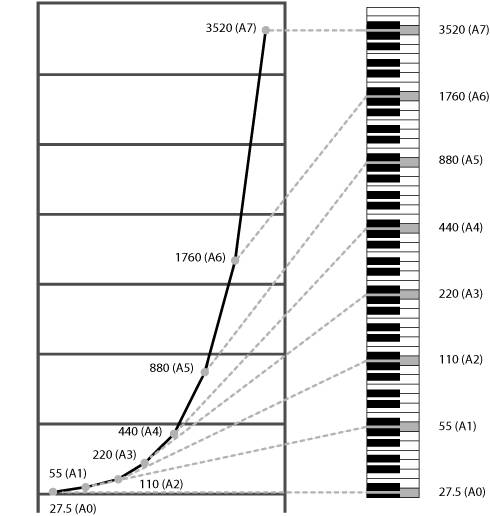
Let's take the simplest interval to calculate, that of the octave, as shown in Figure 1.10 . If you take any frequency number and double it, you'll get the frequency of a pitch an octave higher. For instance, starting with the frequency 220 Hz, the A just below middle C, doubling the frequency to 440 Hz results in the A an octave higher. Likewise, to get the note A an octave lower, you would halve the frequency to 110 Hz. Each time the frequency doubles, the pitch rises by an octave.
Figure 1.10. Octaves look visually equidistant on a piano keyboard, and most musicians would tell you they sound equidistant (and even sound like the "same note," only higher or lower). But the underlying frequency (shown in Hz) doubles each time, indicating that the way we hear is geometric, not linear.
It's not just your ears that make this possible, it's the reality of physical sound. If you cut the wavelength of a string in half, by halving the length of a vibrating string, you'll get a frequency that's twice as high. Keep halving the length of string, and the frequency will continue to multiply by two, the frequency being inversely proportionate to the wavelength. (Or, in the opposite direction, keep doubling the length of string to halve the frequency.) The same thing happens in a software-based synthesizer if we adjust the Transpose parameter to increase or decrease the pitch by an octave: the frequency of the sound being produced by the synthesizer is doubled or halved.
The important related psychoacoustical phenomenon is that we perceive frequencies an octave apart as being very closely related . Musicians would describe the relationship of 440 Hz to 220 Hz as being "the same note, an octave higher." Furthermore, we hear not only the octave itself but the divisions of the octave as being equivalent. The interval between an A and a B sounds the same in the higher octave as in the lower octave, even though the difference between A and B in Hz is twice as great in the higher octave. This way of perceiving pitch space is called octave equivalency . It's the reason Western musicians label pitches using the same note names in each octave (A, B, C, D, and so forth) regardless of how high or low they are. (Other forms of octave equivalency are found in many musical cultures around the world, as well.)
As you can see in Figure 1.10, the underlying numbers produce an exponential curve. The distance in Hz to the high A (a distance of 220 Hz) is twice as large as the distance to the low A (a distance of 110 Hz), and so on up and down the curve. But almost all musicians would say the distances sound the same.
This is obviously important when you're working with the many digital audio software parameters that are labeled in Hz. Transposing a lower pitch up by 100 Hz will sound like a bigger change than transposing a higher pitch by the same amount.
Intervals and tuning
Any two pitches can be related to one another by a ratio called an interval , the octave being the simplest. The ratio of an octave is 2:1. We hear two notes as being "in tune" or "out of tune" with each other based first and foremost on these ratios. It's the ratio of the frequencies, not the raw distance in Hz, which is most significant to our ears.
| | Sounds bad: Acoustical dissonance, which produces the phenomenon called beats, is loosely related to musical dissonance, but the latter is more complex and difficult to quantify because it's related to how intervals are used in various musical styles. The latter topic is not discussed in this book. |
The musical pitches we know, such as the notes of a major scale, are specific, learned frequencies. We've heard them so many times that we've learned the relative intervals formed by certain tunings. If you have perfect pitch, you've even memorized the tunings, but even if you can only sing "Happy Birthday," you've unknowingly memorized a series of intervals. But how did these intervals, the ones that sound good and "in tune," arise in the first place?
First, there are acoustic phenomena that can make two notes sound in tune or out of tune. Close intervals with ratios that can't be described using small whole numbers produce an acoustic phenomenon called dissonance or beats .
Literally, beats are the result of constructive and destructive interference produced by differences in phase between two tones. We perceive these repeated changes in amplitude as a shifting in the sound, which might be very subtle, or a more pronounced, "twangy," rhythmic pattern. (For a dramatic example, think of the out-of-tune old piano in a movie saloon in a Western. We perceive that the piano is out of tune because a piano has three strings for each note, which are supposed to be tuned to the same frequency. When the strings drift out of tune with one another, they produce beats when sounded together.) With pure sine waves of equal amplitude, the frequency of the beating that results when two tones are sounded together is the difference between the frequencies of the two tones. Tones at 440 Hz and 442 Hz, for instance, would produce a difference tone of 2 Hz, which would sound like a regular beating in amplitude twice every second.
Dissonant intervals aren't necessarily bad; on the contrary, they're often used for specific artistic effects. Two slightly detuned sound sources at the unison can be used to create special timbres, as we'll see in the discussion of sound synthesis in Chapter 9. But acoustic dissonance does contribute to our sense of what is and is not in tune.
Because of beating, it's very easy to tell when two pitches don't match at the unison, so the simplest method of tuningwhether you're matching a pitch with your voice or tuning two instruments to the same noteis to tune to unisons. It's also particularly easy to hear the 2:1 ratio of the octave when it is tuned to remove beats, or other simple intervals like the perfect fifth (a ratio of 3:2). Combining these intervals into a tuning system for an entire instrument, however, is far more complex.
Theoretically, it might be ideal to tune to the interval ratios found in the lower harmonics of the harmonic seriesthe ratios of 3:2 (the perfect fifth), 4:3 (the perfect fourth), 5:4 (the major third), 6:5 (the minor third), and so on. The frequencies of the harmonic series correspond closely to musical intervals with which we're familiar ( Figure 1.11 ). The octave, fifth (and by inversion, the fourth), and major and minor thirds are all found in the first six harmonics. In fact, you can tune to simple whole-number ratios for a tuning system that closely matches this series and thus sounds very "tuned"; this system (which is actually a whole family of tuning systems) is called just intonation .
Figure 1.11. The harmonic series consists of the fundamental and the series of harmonic overtones representing whole-number multiples of the fundamental (1x, 2x, 3x, 4x, 5x . . .). The series is based on a fundamental pitch, such as A2 (the A an octave and a third below middle C), which is shown here. The series corresponds loosely to the musical notes shown, but not exactly, because of compromises in the tuning system used by most musicians.

The problem with tuning exclusively to whole-number ratios is that it yields intervals of differing sizes. That creates problems for keyboard instruments in particular, because it makes it difficult to use chord progressions that modulate to different keys. In order to get the same set of intervals in the new key, you'd have to retune the instrument. Starting in the 18th century, as music that moved from one key center to another became more common, Western musicians began using various methods for compromising the ratios of pitches so that all pitches and intervals would sound more or less equally in tune in a variety of keys.
The system used most commonly today, 12-Tone Equal Temperament , makes all adjacent notes on the keyboard sound perfectly equidistant. If you were to play up the white and black notes on a tuned keyboard, each adjacent step should sound the same as every other adjacent step, because the ratio of adjacent pitches to one another is constant. (As usual, we hear geometric ratios as equivalent, not linear differences in Hz.) Unfortunately, this ratio is not based on whole numbers; it's based on the 12th root of 2, which is an irrational number. Strange as it may seem, the ratio is not rational.
As a result, the musical pitches shown in Figure 1.11 only approximate the frequencies in the harmonic series. All of the intervals except the octave are slightly compromised. If you listen closely to a major or minor third in particular, you'll hear beating between the two tones, because the equal-tempered thirds are not the same as the ratios in the harmonic series. But since the tuning system is part of the music most of us hear from birth onward, we take it for granted and don't perceive any out-of-tuneness in its intervals. (Thanks to digital audio technology, it's far easier than ever before to experiment with other tuning systems.)
Musical pitch and digital audio
Certain tasks in digital audio are likely to require that you use musical units rather than audio units. For instance, if you want to transpose a recorded passage to a new key, you'll probably want to do that using terms you're familiar with, like "up a whole-step" or "from D to E" rather than as a ratio or, worse , a unit in Hz. When pitch is described in digital audio applications, the semitone is the most commonly used interval; it's what musicians call a chromatic scale degree or the distance between adjacent notes in an octave on a piano (including both white and black keys). When additional precision is needed, we can divide each semitone into one hundred cents .
If an application displays a parameter in Hz and not in pitch, you may have to convert manually when you need to think in terms of pitch. Fortunately, there are a variety of lookup tables and calculators online. Some applications, like Cycling '74 Max/MSP (www.cycling74.com), even include automatic conversion between the two units. All of these assume the most common tuning system, 12-Tone Equal Temperament. In some situations, it's enough if you remember that doubling the frequency raises the pitch by an octave. For instance, a frequency of 1,500 Hz is an octave above a frequency of 750 Hz.
| | Converting between note names and Hz: You'll find a handy online converter at www.phys.unsw.edu.au/~jw/notes.html. |
How We Hear Loudness
As with musical pitch, calculating relative loudness is complex because of the details of how we hear.
The terms "amplitude" and "loudness" are often used interchangeably, but although they're related, they're not the same thing. Amplitude is a relative measure both of the physical properties of sound (the relative displacement of air pressure) and of the relative strength of audio signals (both digital and analog). Loudness, on the other hand, is a subjective terms that's dependent on perception. It's what seems loud to you based on the physical capabilities of your ear and the way your brain processes sound.
The human ear is capable of detecting an extraordinary range of amplitudes, which in sound is measured as sound pressure level . If we measured these numbers directly, we'd have to work with some decidedly inconvenient numbers: the power range of the human ear is a ratio of approximately ten trillion to one. Unless you like numbers with lots and lots of zeros, you'll probably want a more convenient scale with which to label a volume fader.
Decibel scale
The basic mathematical method of turning this huge range of numbers into a more manageable range is to use a logarithmic rather than a linear scale. Without getting too far into the underlying mathematics, this means that instead of marking off increments in a numbering system like 1, 2, 3, 4, 5, 6 . . ., you use those simple numbers to represent bigger numbers (the sound pressure level ratios with increasing numbers of zeros on the end).
The original unit for measurements of this type was called the bel , after Alexander Graham Bell. Even that number proved to be a little too large for use with sound, so engineers simply eliminated one last zero, giving us the decibel (dB) , which is equal to 1/10 of a bel.
You're probably already familiar with another logarithmically derived scale, the Richter scale, which is used to measure the intensity of earthquakes. Like the Richter scale, decibels are a generic measure of ratio. Since we're measuring ratios and not a simple quantity (as with inches or kilograms), the key questions are ratio of what unit, and relative to what? Without a point of reference, the scale doesn't mean anything.
The relative point from which the decibel scale is measured is an arbitrary point that's called 0 dB. When we say that a sound measures 0 dB, we're not necessarily talking about zero amplitude.
Different uses, different scales
Two basic forms of decibels are used in audio, those used to measure acoustic phenomena relative to human hearing and those that measure signal strength in electrical systems. Comparing sound pressure to signal strength is like comparing apples to oranges, even though both are routinely measured in decibels. We all understand the joke in the movie This Is Spinal Tap when the character Nigel ignorantly points to a guitar amplifier that "goes to eleven" instead of ten. In the end, units related to loudness are literally all relative.
The dB (SPL) scale measures sound pressure level relative to human hearing. It sets zero as the lowest sound pressure level at which most people can hear a sound. (Again, this is relative, so if you have especially sensitive ears, you may be able to hear sounds that would be measured as slightly below 0 dB.) For electrical signal strength, a variety of units measure either power (including units like the dBm; "m" is short for milliwatt) or relative voltage level (units like dBu and dBV). The good news is you probably won't need to know the difference between dBm and dBu. These letters are tacked on the end of these units in contexts like technical specifications of audio equipment so that engineers know what the reference level of that equipment is.
Loudness and digital audio
In audio software, decibels are usually a relative measure of the strength of an audio signal. For instance, in a mixer view in an application like Digidesign Pro Tools or Cakewalk SONAR, 0 dB would be not the smallest sound you could hear, but an arbitrary measure of level within the application. The signal of a given waveform might be a smaller value (a relatively weaker signal, measured as a negative dB value) or a slightly higher value (a relatively stronger signal). In some applications, 0 dB is the highest possible peak the application can handle, and everything else is measured as lower than 0 dB.
Decibel ratios only loosely correlate to the way we perceive significant volume changes. An increase of 3 dB doubles the relative sound pressure or power level of a sound; a decrease of 3 dB halves it, but the perceived change in loudness is fairly subtle. A change of one or two dB is often undetectable. To get a change that sounds twice as loud, it's often necessary to increase the volume level by 20 or 30 dB.
Not all frequencies are created equal, either. Our ears are most sensitive to sounds toward the center of the pitch spectrum, closer to the frequency range of speech, and less sensitive to sounds at lower and higher frequencies. That's the reason the "loudness" setting on many home stereos and consumer audio devices will boost the bass and treble, leaving the middle spectrum untouched. By boosting the bass and treble, a loudness curve has the opposite bias of your hearing, which is more sensitive to the middle frequencies. It boosts the frequencies you have the most difficulty hearing at low listening volumes. The resulting effect sounds fuller and more present, even though the volume for the whole sound has not been boosted by as much as you think it has. (Incidentally, a loudness contour will therefore have very little effect at high listening volumes , because your ears are less biased to the center when sounds have greater amplitude.) The equalization section of Chapter 7 details some of the other ways in which amplitude changes to different frequencies impact perceived sound.
| | Standard measurement of amplitude: Digital audio software usually uses decibels (dB) as a relative indication of amplitude. |
What does matter is the volume change you perceive when you make a change in decibel level. So should you pull out your scientific calculator and start punching up logarithms? Of course not; the decibel was invented to save you that trouble. Instead, you'll most likely develop an intuitive sense of how a certain change adjusts the sound in certain frequency ranges. Sound engineers routinely talk about "boosting the mids [middle frequencies] by a couple of dB," for instance.
|
How we hear timbre
As discussed earlier, most sounds contain energy at multiple frequencies, but our ears fuse these together and experience them as a single sound. It's the combination of these component energies that we hear as timbre , the color or character of a sound. (That's pronounced tam-burr , not "timber.")
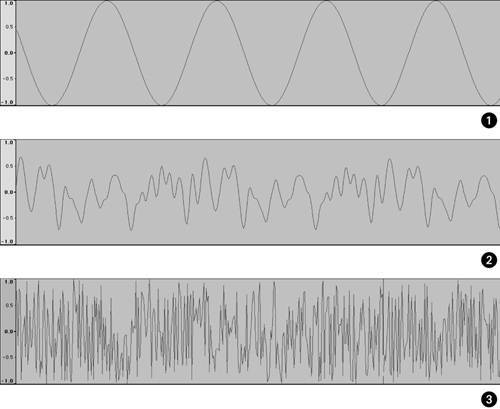
The timbre of a sound depends entirely on the frequencies of the partials in the sound and the amount of energy at each frequency (the amplitude of each partial). Different partials will typically last for different lengths of time, as well, so part of what we hear as timbre is the way this frequency content changes over time. The energy of these different partials over time is what allows us to tell the difference between the sound of a tuba and the sound of an electric guitar. This overall picture of the content of the sound is commonly called the spectrum of the sound, the distribution of energy across the range of audible frequencies. As you add energy to the overtones of a sound, the resulting waveshape (as you'd see it on an oscilloscope or in a software program) changes. A simple sine wave, as you've seen, has steady, repeated increases and decreases in air pressure resulting in a single frequency with no overtones. As you add harmonics above this pure tone, the resulting waveshape becomes more complex, as shown in Figure 1.12. As inharmonic overtones are added, the periodicity of the wave will disappear, and the sense of a defined, clearly audible pitch will begin to be reduced. The more inharmonic content is present, the less well defined the pitch of the sound will be.
Figure 1.12. When a waveform view in software is zoomed in close enough to allow details to be viewed , you can see the individual periods (cycles) of the wave. A pure sine wave (1) has a simple, repeating period. With added harmonics (2), the periodicity remains, but the shape of the wave becomes more complex. You'll still hear this sound as pitched, but the perceived timbre will be richer. With noisy sounds, like the synthetically generated white noise shown (3), there's no repeated period at all. With no discernible period, you'll no longer hear the sound as pitched; the result will sound like wind or static.
In contrast to pitched tones, noise lacks perceptible periodicity entirely, as shown in Figure 1.12. Sounds like electrical static and wind are mostly noise in their sound content. On a frequency spectrum, they would have no noticeable harmonics and a fairly even distribution of energy at all frequencies. Theoretical "white noise" has equal energy at all frequencies: it's "white" in the same sense that white light contains energy at all visible wavelengths .
These qualities of timbre become all the more significant when you begin designing your own sounds and virtual instruments. For an extended discussion with hands-on examples, see Chapter 9.
What Sound Looks Like in Software
Now that you've learned the basics of the physics of sound, how will you deal with sound in digital audio software? So far, we've dealt with three basic elements:
-
Time: Without time, you can't have pitch (since frequency is just repeated oscillations over time) or music (which also exists in time).
-
Amplitude/relative air pressure deviation: Amplitude is essential to determining the strength of sound materials and to perceived loudness.
-
Frequency content and partials: We hear the strengths of different partials in the sound over time as its timbre.
Much of the time, digital audio software displays the first two elements onscreen. Figure 1.13 shows a typical waveform view in audio software, which shows a representation of signal strength or air pressure on the y-axis and time on the x-axis.
Figure 1.13. A typical wave editor view of a waveform, shown here in Apple Soundtrack Pro. When the display is zoomed out to the time level you'd most often use for editing, you won't be able to see individual wave periods, but you will be able to see overall changes in amplitude.
The height of the waveform on the y-axis of the graph should be roughly analogous to the changes in air pressure of the actual sound, as a result of the digital recording process described in the section "Sound in Digital Form" later in this chapter. Any deviation above or below the center line represents amplitude, as you saw earlier. The display shows the strength of the recorded digital signal, although the labels on the y-axis are often fairly obscure, labeled simply as -1.0 to zero to 1, or -100% to 100%, rather than something specific like decibels. If they are labeled in decibels, you may see something like 0 dB for the maximum, and a negative value like -96.3 dB, representing the dynamic range of the digital audio software. Some programs provide y-axis labels in exact sample values, such as -32,628 to 32,627, although since this type of data is a little hard to grasp, it's much less common.
| | On the DVD: Basic waveform editors are useful "Swiss Army knife "-style tools for working with digital audio. Audacity, included on the DVD, is a free, open -source, audio-editing package available for Windows, Linux, and Mac OS X. |
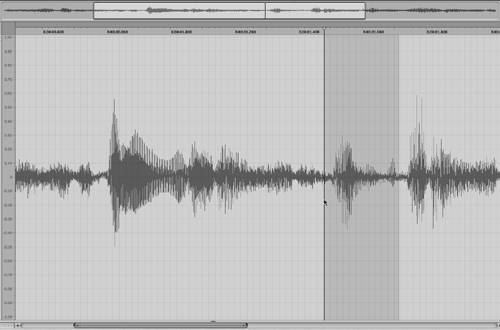
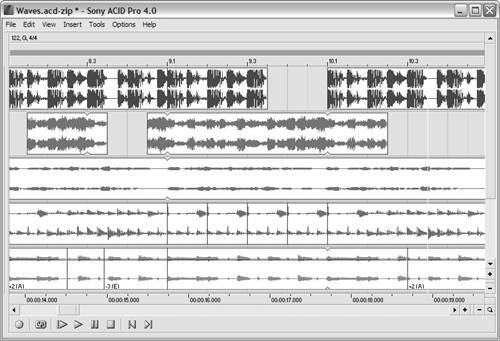
When the display is zoomed further out to give you an overview of a longer segment of sound, you won't see the individual oscillations of the waveform, but you will see the overall amplitude profile over time. You'll be able to see where words in a sung or spoken recording begin and end, where drum hits or bass notes happen, and so on. Figure 1.14 shows a typical screenshot from Sony ACID Pro (http://mediasoftware.sonypictures.com) with an overview of a song arrangement.
Figure 1.14. Waveform overviews as they appear in a song arrangement in Sony ACID Pro. Here, you can see the elements of your song as they relate to one another (beats, notes, and other elements as they appear in the amplitude of the waveforms).
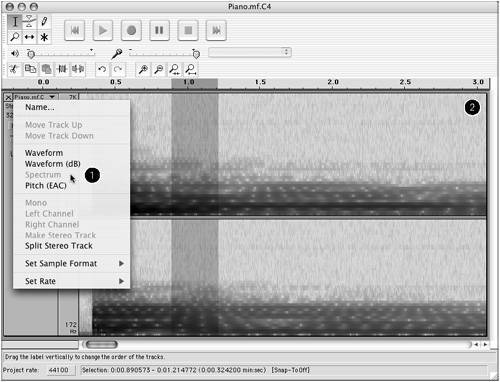
Showing air pressure and time in a basic waveform view isn't the only way to represent sound onscreen. Many programs allow you to view the frequency spectrum of the sound, which is more useful for seeing the timbral qualities of the sound you're editing and fine-tuning parameters of effects and edits in Hz, as shown in Figure 1.15 .
Figure 1.15. Select the Spectrum view from the drop-down menu next to a waveform (1), and Audacity displays a frequency-versus-time graph in which amplitude is displayed as shades of gray (2). The spectrum of a real-world sound contains a range of pitched components that contribute to the color of the sound. You can use this view in Audacity to edit and filter a sound.
|