How Sound Works

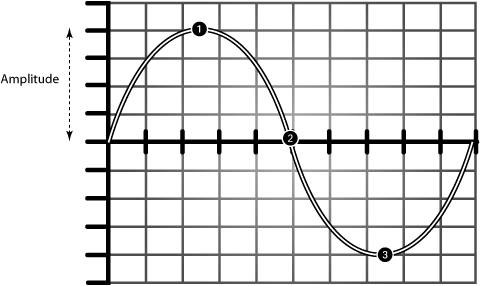
We're so used to being surrounded by sound that we take it for granted, but what is sound, exactly? In terms of the physical event, sound is a series of vibrations that travel through some medium. Unless you're planning on playing your next show underwater in a swimming pool, it's safe to say that the medium is probably air. For practical purposes then, we can describe sound as alternate areas of slightly more compressed and slightly less compressed air that move outward from a source.

When you hit a drum head, for instance, the skin of the drum vibrates, moving rapidly up and down ( Figure 1.1 ). Materials like drum heads and strings can vibrate because they're elastic; you can create sound by plucking a rubber band for the same reason. With each outward movement of the drum head, air molecules around the outer surface of the drum become more densely packed, increasing the air pressure slightly. This increased air pressure is called compression . With each inward movement, the molecules spread out again, dropping the air pressure, which is called rarefaction . The sound of a drum dies away quickly, but even so, the drum head moves up and down a number of times before it comes to rest, creating a series of compressions and rarefactions. The typical waveform graphs you'll see in digital audio software and physics textbooks alike simply show us how these compressions and rarefactions alternate over time. The result looks like the wavy line shown in Figure 1.1.

Figure 1.1. As a sound source vibrates, it causes rapid fluctuations in air pressure around it. As a vibrating body like a drum head expands outward (1), it packs adjacent air particles together ( compression ). As it rebounds to a neutral position (2), air pressure returns to normal. As it moves inward (3), air pressure decreases ( rarefaction ). As this process repeats, waves of sound spread outward through the air from the source. In digital audio software, we can observe a graph that represents these air pressure fluctuations over time (4).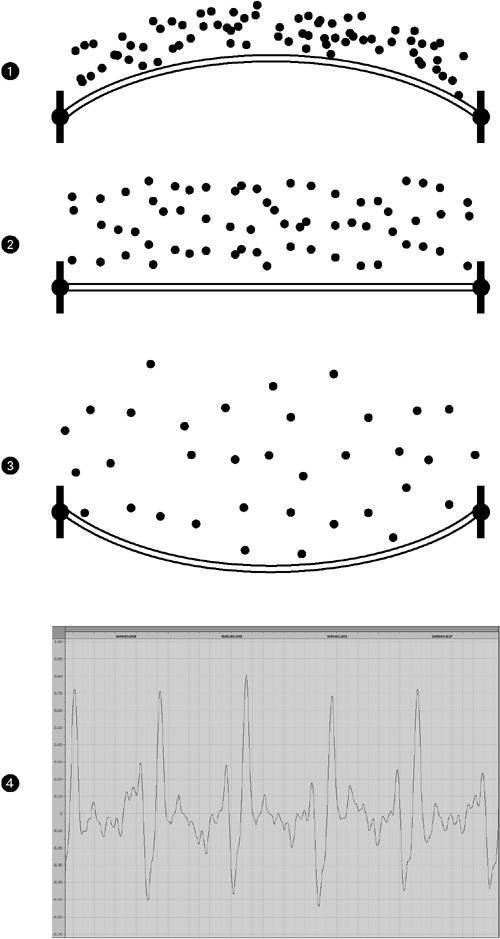

These changes in pressure don't just occur immediately around the source, or you wouldn't hear anything. The alternations in pressure move outward from the drum (or whatever happens to be vibrating) through the air: they propagate outward. These outward-moving variations in air pressure are called sound waves . The waves of vibrations are transmitted much like ripples in a pond, although it's important to realize that unlike water waves, waves of sound don't move up and down. Instead, they're longitudinal waves : these waves involve forward-and-back vibrations of air in a line between the listener and the sound source ( Figure 1.2 ). Once the drum stops vibrating, the waves dissipate, the air pressure becomes stable, and the sound stops.

Figure 1.2. Waves of compression and rarefaction spread outward from a source through the air, a phenomenon called wave propagation .

It's the wave that moves outward from the source, not the air in the wave. The air vibrates, but when you hear a note from a cello, you're not hearing air that's traveled from the cello to you, any more than when a wave hits the beach in Australia its carrying water from Hawaii. The energy of the vibration is what actually travels , not the water.

Without some material to vibrate, you can't have sound. The answer to the old riddle, "If a tree falls in a forest and there's no one there to hear it, does it make a sound?" is, in fact, yes. The sound of the tree falling radiates outward through the surrounding air as the air molecules around the tree vibrate. The only way the tree wouldn't make a sound would be if there were no air or other material to carry the vibrations.

The science of how sound travels in the air and in physical spaces is called acoustics ; it's the study of what physically happens to sound waves under different conditions in the real world. (When there is someone around to hear a sound, an additional set of issues comes into play; the study of psychoacoustics deals with the perception of sound.)

Acoustics is a branch of physics, but acoustical engineers work with environments that are very familiar to musicians , like concert halls and recording studios . Acousticians need to understand what will happen to sound from an orchestra when it bounces off walls, for instance, or how raucous a restaurant in a soon-to-be- constructed building will sound when it's full of diners. You might not be planning a career in acoustical engineering, but a basic understand of how sound works will help you decide where to place your mic while recording vocals, how to configure a digital reverb effect so your track sounds realistic, and how to perform countless other tasks .

Dimensions of a Sound Wave

To work with digital audio tools, we need to be able to describe sound in ways less vague than simply "areas of air compression" or "vibrations." As we talk about digital audio, we'll be using two key measurements of sound: amplitude and frequency .

Amplitude

The change in air pressure of each compression or rarefaction is a sound wave's amplitude . When we measure or describe amplitude, we're describing the amount by which the air pressure changes from the normal background air pressure, whether positive or negative. Amplitude is a very real phenomenon: if you've ever been at a concert with a loud, booming bass and felt vibrations in your chest, what you felt were the literal, large-amplitude vibrations of the sound, which made your body vibrate.

Using digital audio tools, we can map these up-and-down changes in pressure over time; we'll get a wavy line more or less like the one shown in Figure 1.1. The distance the wavy line moves above or below the straight line in the center is the change in pressure, the amplitude ( Figure 1.3 ). Each upward thrust is called a peak or crest , and each downward dip is called a trough because the graph looks like a wave of water in the ocean. The spot where the wave is in a neutral position, representing no change from the background air pressure, is called a zero crossing . The overall shape of crests and troughs over time is called a waveform . With very few exceptions, every digital audio device you'll ever use generates, processes, or otherwise handles waveforms. (One important exception is MIDI, which is introduced at the end of this chapter and discussed more fully in Chapter 8.)

Figure 1.3. Mapping the change in air pressure over time results in a graph that's shaped like a wave. Each compression, an increase in air pressure, is represented by a crest (1). As air pressure returns to the normal level, it crosses the center line (2), a zero crossing. Each rarefaction, a decrease in air pressure, is represented by a trough (3).

Frequency

As a series of air pressure waves reaches your ear, you perceive continuous sound, not individual fluctuations in air pressure. Your ear and brain can count in a remarkably accurate way how many wave crests and troughs occur in a given span of time.

Frequency vs. pitch: Frequency is not quite the same as musical pitch, but we can treat them as roughly interchangeable terms. Pitch is usually expressed in musical terms, using note names like C and D. Frequency is usually expressed in Hz.

When the peaks and troughs are closer together, so that more of them hit your eardrum in quick succession, we say the sound is higher in pitch; when the peaks and troughs are farther apart, so that fewer of them reach your eardrum in the same span of time, we say the sound is lower in pitch ( Figure 1.4 ).

Figure 1.4. We hear changes in frequency based on how rapidly the air pressure oscillates. The more crests and troughs of a sound wave reach your ear in a span of time (the greater the frequency, or shorter the wavelength), the higher the pitch.

The scientific term for how many peaks (or troughs) of a sound pass a given point within a given time is frequency . Frequency is usually described in cycles per second. A cycle consists of one upward crest and one downward trough. The unit for measuring the number of cycles per second (cps) is the Hertz (Hz). A measurement of frequency in Hertz tells us how many crest/trough pairs occur in the waveform during a time interval of one second.

Standard measurement of frequency: Hertz (Hz), or cycles per second; the number of complete periods (one upward crest and one downward trough) that occur each second.

Another useful way to talk about sound waves is in terms of their wavelength , the distance between adjacent crests (or between adjacent troughs). Wavelength is inversely proportional to frequencythat is, sound waves with long wavelengths have low frequencies, while sound waves with short wavelengths have high frequencies. It's easy to see why: if the distance between adjacent wave crests is greater, fewer of them will arrive at your ear in a given amount of time. Figure 1.4 represents this relationship visually.

The Doppler Effect

When a sound source is in motion and the person hearing the sound is at rest (or vice versa), the perceived pitch changes. That's the reason a train's horn sounds as if it's changing in pitch as it passes you: the waves are pushed closer together (for a higher frequency) as the train moves toward you and spread farther apart (for a lower frequency) as the train moves away. This phenomenon is called the Doppler effect . Digital audio software can replicate this effect, a trick used by sound designers for film and TV. (The effect is also used, amazingly enough, by astrophysicists to determine how quickly nearby stars are moving in relation to us. The observed wavelengths of the stars' light depend on their motion.)

How fast is sound? In dry, room-temperature air, sound travels about 1,125 feet (343 meters ) every secondonly marginally faster than a typical commercial airliner's cruising speed. That means that in a large space you can hear the delay of a sound bouncing off a wall. This delay time is used in digital audio to create realistic models of acoustic space.

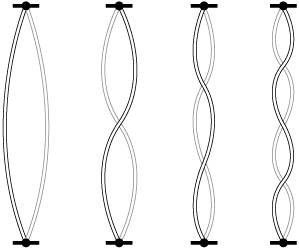
Sine Waves and the Geometry of Sound

Real-world waveforms aren't perfect, regular up and down oscillations, nor do they have just one frequency: sound almost always has energy at multiple frequencies simultaneously . This fact is central in the construction of digital audio devices such as equalizers and filters (Chapter 7). However, audio engineers have found it extremely useful to have a basic waveform that can be used as a sort of benchmark or building block to describe more complex waveforms. This basic waveform, the sine wave , oscillates repeatedly at a single frequency, and has no sound energy at any other frequency.

Meet the sine wave

The sine wave is a basic, periodic wave (one that repeats at regular intervals). It sweeps up and down in a motion that's a bit like the shape of the humps and dips of a roller coaster ( Figure 1.5 ). Sounds that we'd describe as "pure," like a flute playing without vibrato, a person whistling, or a tuning fork, all approximate the sine wave. It's even the ideal wave shape for the electricity in your home's power outlets.

Figure 1.5. Computers are capable of producing an approximation of a pure sine wave, as represented here in the waveform display in Apple Soundtrack Pro (top). Shown in a graph of frequency content over time (bottom), this sine wave is a single horizontal band; unlike other sounds, the sine wave carries energy at only a single frequency. The haze around the horizontal band is not due to the presence of other frequencies in the sine wave; it's caused by the limitations of the analysis process.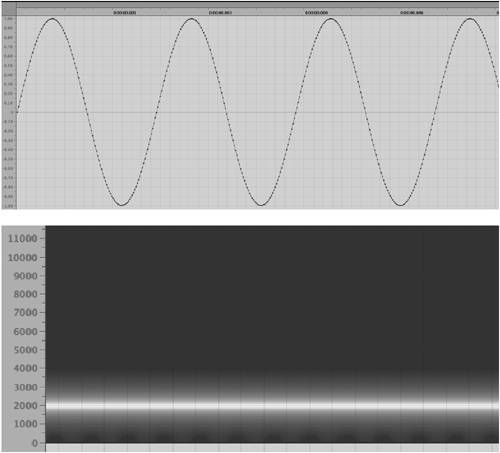

The sine wave is the wave shape you'll most often see illustrated , as in Figures 1.3 and 1.5, but it's not just useful in sound and physics textbooks: any real-world sound can be analyzed mathematically as a combination of sine waves, a property that underlies many digital audio techniques. As a result, you can begin to understand how the complex, irregular world of real sound can be understood as a combination of single frequencies.

Overtones

Most of us would intuitively assume the sound of a single musical note has one pitch, and thus one frequency. In fact, when you pluck the string on a guitar, it produces a single pitch, but the string vibrates not just at one frequency but at multiple frequencies simultaneously ( Figure 1.6 ). The enormous variety of sounds in the real world (and in digital audio applications) is due to the complex blending of these various frequencies.

Figure 1.6. A string or other vibrating body doesn't just vibrate at a single frequency and wavelength; it vibrates at multiple frequencies at once. This string is vibrating not only at the full length of the string, but also in halves , thirds , fourths, and so on.

For instance, a string like the one shown in Figure 1.6 not only vibrates at its full length, but at the halves of its length, the thirds of its length, and so on, all at the same time. As the wavelengths decrease by whole-number fractions ( ½, 1/3 , ¼, 1/5 . . .) the frequencies inversely increase by whole-number multiples (2x, 3x, 4x, 5x . . .), so the frequencies that result from the vibrations represented in Figure 1.6 will be successively higher as the wavelengths get shorter.

The lowest of these frequencies (usually the one we think of as the "note" of the sound) is called the fundamental frequency, and the frequencies above the fundamental are called overtones (the tones "over" the fundamental) or partials (since they make up part of the whole sound).

The overtones shown in Figure 1.6 have a special property: each frequency is a whole-number multiple of the fundamental frequency. Any whole-number multiple of the fundamental frequency is called a harmonic . This series of frequencies (twice the fundamental frequency, three times the fundamental, four times the fundamental . . .) is called the harmonic series or overtone series . The sounds of many tuned musical instruments, like the piano and violin, contain major portions of energy concentrated at or very near the harmonics.

Because the frequencies of the harmonic series are whole-number multiples of the fundamental, a sound composed solely of energy at these frequencies will remain perfectly periodic; the resulting waveform will repeat without changing at the frequency of the fundamental.

Not all overtones are harmonics, however. In between the harmonics, real-world sounds often have overtones that aren't as closely related to the fundamental. These overtones are called inharmonic overtones or, more often, simply partials . (Note that that doesn't mean all partials are inharmonic. All harmonics are partials, but not all partials are harmonics.) Because inharmonic partials aren't related to the frequency of the fundamental, the wave resulting from a fundamental frequency and inharmonic frequencies above it will be irregular over time; it won't have a single, repeating period. Instruments like a wire-stringed guitar, for instance, contain many inharmonic overtones; instruments with complex timbres like cymbals contain even more. ( Figure 1.7 shows comparisons of different sounds.) You'll see these irregularities when you look at the waveform of the sound in a digital audio program.

Figure 1.7. Any sound that's not a sine wave has partials, but different sounds vary in harmonic and inharmonic content, as shown here in sound samples viewed by their frequency spectrum. In these diagrams, frequency is displayed on the y-axis, time is displayed on the x-axis, and the amplitude of the partial is shown by the brightness of the area. The pure-sounding small bell (1) is strongest at the fundamental, with almost no inharmonic content and a few clear harmonics. A melody played on a B sendorfer grand piano has richer harmonic content (2); the ladder-like effect shows the harmonics above each note of the melody. An alarm bell (3) mixes harmonic content (the brighter lines) and inharmonic content (the gray areas in between). A pattern played on a ride cymbal is almost all unpitched noise (4). The bright, leading edges are the initial crash of the stick hitting , but even as the sound decays it retains a mixture of inharmonic content evidenced by the gray areas.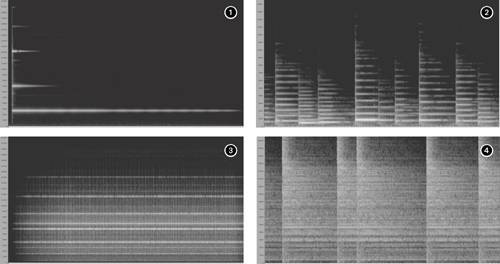

We don't usually hear the different overtones independently; they combine to form a more complex waveform. However, using a mathematical technique called a Fourier transform , it's possible to analyze any complex waveform as being made of a number of simple components , all of which are sine waves. This process underlies many techniques in digital processing, like the spectrum views shown in Figure 1.7, and many digital effects. (See "Fast Fourier Transform: Behind the Scenes of Spectral Processing" in Chapter 7 for one specific example; many other digital processes rely on Fourier transforms as well.)

You say first overtone, I say second harmonic: Because most sounds contain a series of partials at higher and lower frequencies, we can give a number to each progressively higher partial. But the way we count them can be a little confusing. The first overtone is the first partial above the fundamental. The fundamental, which is a partial, is itself a harmonic (because its frequency is a whole-number multiple of itself, the whole number in this case being 1), so the fundamental counts as the first harmonic. Thus, the first overtone (an octave above the fundamental) is the second harmonic. The second overtone is the third harmonic, and so on.

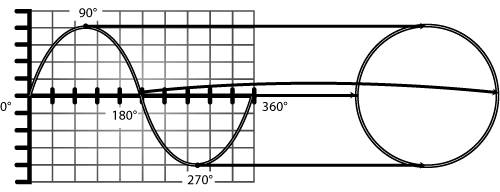
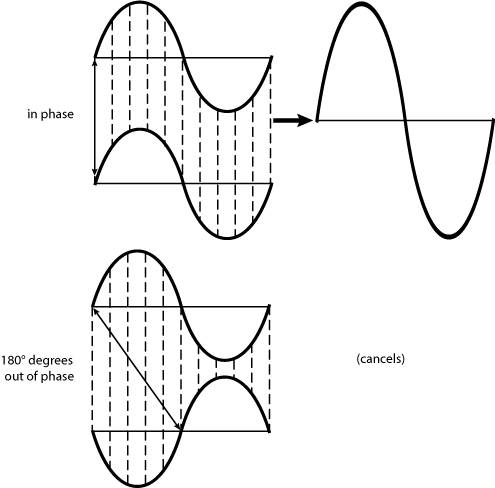
Phase

So far, we've looked at the amplitude of a waveform (the increase or decrease in air pressure) and the frequency (the number of complete up and down oscillations in a given amount of time). These are useful dimensions, but neither of them tells us exactly when the oscillation of a wave is up (higher air pressure) or down (lower air pressure). To completely describe a waveform, we need a third dimension: the phase of a waveform is the position of the wave within its complete up-and-down cycle (period). At first glance, the whole business of waveform phase may seem too scientific for musicians to worry about, but it has very practical implications, as you'll see in later chapters. Knowing about phase becomes important when you're setting up multiple microphones to record an acoustic instrument, for example.

Phase is described in trigonometric terms as degrees of arc relative to a circle. Why have we switched from waves to circles? Because the sine wave is essentially a perfect circle unfolded geometrically into a wave. The sine function comes from trigonometry, the branch of mathematics that deals primarily with right triangles and circles. Aside from being used to calculate the dimensions of angles and sides in triangles , the sine function is used to determine the position of any point on a circle. That makes it convenient for our purposes in sound, because it lets us accurately refer to specific points along a sine wave as it oscillates up and down.

One period of a sine wave is equivalent to one complete rotation of a circle, so you can talk about any point along the sine wave simply by referring to a quantity in degrees from 0 to 360 ( Figure 1.8 ). The beginning of the period starts at 0 °, proceeds to the top of the crest at 90 °, back to zero amplitude at 180 °, to the bottom of the trough at 270 °, and back to zero amplitude at 360 °. That position along the period of the sine wave is the waveform's phase.

Figure 1.8. You can easily label a period of a sine wave in relation to a circle from 0 to 360 degrees. Any point can be calculated in degrees, but the easiest to spot are 0 °, 90 °, 180 °, 270 °, and 360 °. The 360 ° point is the same as the 0 ° point, because it's the start of a new period.

Our ears can't ordinarily detect the phase of sound waves, but phase is just as important as frequency and amplitude for another reason. A waveform's phase determines what happens when it's combined with a similar wave, an event called wave interference .

When waves collide

Real-world sound, as noted earlier, rarely consists of a single sine wave emanating from a single sound source: most sound sources produce energy at multiple frequencies. In addition, different sound sources often combine, and it's the more complex, composite waveform that reaches your ear. Just as dropping several pebbles into a pond creates complex, overlapping waves on the surface of the water, the combination of different overtones and different sounds changes the resulting wave shape.

When waves pass through one another or are superimposed, they interfere . (This is also sometimes called the superposition of waves.) Interference can be constructive interference, in which the addition of the two waveforms results in a new wave of greater amplitude, or destructive interference, in which the resulting amplitude is less than that of either wave by itself.

If a peak of one waveform combines with the peak of another waveform, or a trough with another trough, the amplitude of the two waveforms will be added, making the composite sound louder. However, if a peak combines with a trough, the amplitude of the waves will be reduced, making them sound softer. If the peak and the trough are of equal amplitude, they'll cancel each other out, resulting in a zero amplitudethat is, in silence ( Figure 1.9 ).

Figure 1.9. When sine waves of equal amplitude interfere and are in phase, they combine, doubling in amplitude (top). If they are 180 ° opposite in phase, they cancel each other out (bottom), resulting in a zero amplitude.

Whether you're making a recording using multiple microphones or adding waveforms by mixing them in a digital audio program, you need to understand this basic fact: when two waves are added, the amplitude of the resulting wave depends on the phase relationships of the two original waves. In other words, it's the phase of two sine waves that determines whether those waves interfere constructively or destructively. Two sine waves of equal amplitude and frequency that are in phase , meaning crests and troughs are aligned with one another, will combine to form a sound that's twice as loud. When the same two sine waves are 180 degrees out of phase , meaning crests are aligned with troughs, the result will be silence. (The cancellation of out-of-phase waveforms is called, oddly enough, phase cancellation .) If the phase of two sine waves with equivalent amplitude and frequency is neither perfectly in phase nor perfectly out of phase, there will still be cancellation, but only partial cancellation: two waveforms that are 90 degrees out of phase will be weakened, but not silenced.

The same principles apply to real-world sounds composed of various partials, but for each individual partial. Wave interference between real-world sounds will only result in complete phase cancellation if all of their partials have exactly the same amplitude and frequency, and if all those partials are 180 degrees out of phase. For that reason, it's extremely unlikely that you'll experience complete phase cancellation in the real world. More often, only some partials will be strengthened or weakened, so that the resulting mix of two sounds will be a little thinner or quieter at some frequencies and a little louder at others because of constructive or destructive interference.

Phase cancellation can become a problem in digital audio work, however, making sounds softer or thinner in color than desired. On a P.A. system in a live performance situation, for instance, speakers situated too close to a live sound source (like drums) can cancel out some of the natural sound from the instrument by overlapping that natural sound with out-of-phase amplified sound. You can use this effect to your advantage: by adjusting the placement of the speakers , you can employ constructive interference from in-phase sounds as reinforcement, making the mix of natural and amplified sound stronger.

Why phase cancellation matters: Unwanted phase cancellation can deaden certain sounds. You'll need to be mindful of the effects of phase cancellation whenever working with sound, but especially when recording or performing with multiple mics (see Chapter 6) or mixing (see Chapter 10). Wave interference and phase can also be used creatively in synthesis (see Chapter 9).

A similar problem can occur when recordings are made using multiple microphones. This is particularly an issue with stereo recording or recordings of instruments like acoustic guitar and piano, when the goal is to mix the same source sound into multiple mics. The sound can arrive later at one microphone than the other, meaning you'll have two out-of-phase versions of a similar signal. When the signals from the two mics are blended, you won't hear silence, but you may hear a thinner or quieter sound than you expected. Usually, you can diagnose such problems by comparing the sound of a single mic to the mix of all of the mics, and then adjust microphone placement until you hear the mix you want.

Phase cancellation isn't always a bad thing. The muffler on your car is composed of a series of metal tubes and a resonator chamber that are designed to maximize destructive interference between waves in order to reduce the noise of exhaust from the engine. Active cancellation circuitry in noise-reducing headphones intentionally produces out-of-phase waves to deaden the sound of unwanted external noise; a microphone picks up the external noise and the headphones play back the sound out of phase.

In fact, you can use phase cancellation creatively by intentionally detuning two oscillators from one another in a synthesizer; see Chapter 9 and the discussion of detuning in the section "Intervals and tuning," later in this chapter.