8.5 Canonical Forms

Because there is a finite number of unique Boolean functions with n input variables , yet an infinite number of possible logic expressions you can construct from a finite number of functions, there is an infinite number of equivalent logic expressions. To help eliminate confusion, logic designers generally specify a Boolean function using a canonical , or standardized, form. For each different Boolean function, we can choose a single canonical representation of that function.

There are several possible ways to define a set of canonical representations for all the possible Boolean functions of n variables. Within each canonical set, there is a single expression that describes each Boolean function in the system, so as long as you only utilize functions from a single canonical set, all of the functions in the set will be unique. We will discuss only two canonical systems in this chapter and employ only the first of the two. The first is the so-called sum of minterms and the second is the product of maxterms. Using the duality principle we can convert between these two.

As mentioned earlier, a term is either a single literal or a product (logical AND) of several different literals. For example, if you have two variables, A and B, there are eight possible terms: A, B, A', B', A'B', A'B, AB', and AB . For three variables we have 26 different terms: A, B, C, A', B', C', A'B', A'B, AB', AB, A'C', A', AC', AC, B'C', B'C, BC', BC, A'B'C', AB'C', ABC', ABC', A'B'C, AB'C, A'BC, and ABC . As you can see, as the number of variables increases, the number of terms increases dramatically. A minterm is a product containing exactly n literals, where n is the number of input variables. For example, the minterms for the two variables A and B are A'B', AB', A'B, and AB . Likewise, the minterms for three variables A, B, and C are A'B'C', AB'C', A'BC', ABC', A'B'C, AB'C, A'BC, and ABC . In general, there are 2 ⁿ minterms for n variables. The set of possible minterms is very easy to generate because they correspond to the sequence of binary numbers (see Table 8-6).

Table 8-6: Generating Minterms from Binary Numbers
Binary Equivalent (CBA)	Minterm
000	A ² B ² C ²
001	AB ² C ²
010	A ² BC ²
011	ABC ²
100	A ² B ² C
101	AB ² C
110	A ² BC
111	ABC

We can derive the canonical form for any Boolean function using a sum (logical OR) of minterms. Given F ₂₄₈ = AB + C the equivalent canonical form is ABC + A'BC + AB'C + A'B'C + ABC' . Algebraically, we can show that the canonical form is equivalent to AB + C as follows :

 ABC + A'BC + AB'C + A'B'C + ABC' = BC(A + A') + B'C(A + A') + ABC' By P4                                   = BC * 1 + B'C * 1 + ABC'         By Th15                                   = C(B + B') + ABC'                By P4                                   = C + ABC'                        By Th15 & Th4                                   = C + AB                          By Th11

Obviously, the canonical form is not the optimal form. On the other hand, there is a big advantage to using the sum of minterms canonical form: it is very easy to generate the truth table for a function from this canonical form. It is also very easy to generate the sum of minterms canonical form equation from the truth table.

8.5.1 Sum of Minterms Canonical Form and Truth Tables

To build the truth table from the sum of minterms canonical form, follow these steps:

Convert minterms to binary equivalents by substituting a 1 for unprimed variables and a for primed variables:

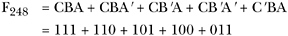
Place the number 1 in the function column for the appropriate minterm entries:

C	B	A	F = AB + C

		1
	1
	1	1	1
1			1
1		1	1
1	1		1
1	1	1	1

Finally, place the number in the function column for the remaining entries:

C	B	A	F = AB + C

		1
	1
	1	1	1
1			1
1		1	1
1	1		1
1	1	1	1

Going in the other direction, generating a logic function from a truth table, is almost as easy. Follow these steps:

Locate all the entries in the truth table with a function result of one. In this table, these are the last five entries. The number of table entries containing ones determines the number of minterms in the canonical equation.
Generate the individual minterms by substituting A, B, or C for ones and A', B', or C' for zeros. In this example, the result of F ₂₄₈ is one when CBA equals 111, 110, 101, 100, or 011. Therefore, F ₂₄₈ = CBA + CBA' + CB'A + CB'A' + C'AB . The last entry in the table contains all ones, so we generate the minterm CBA . The second-to-last entry contains 110, so we generate the minterm CBA' . Likewise, 101 produces CB'A , 100 produces CB'A' , and 011 produces C'BA .
The logical OR and logical AND operations are both commutative, so we can rearrange the terms within the minterms as we please , and we can rearrange the minterms within the overall function as we see fit.

This process works equally well for any number of variables, as with the truth table in Table 8-7 for the function F _53,504 = ABCD + A'BCD + A'B'CD + A'B'C'D .

Table 8-7: Truth table for F ₅₃ ,504
D	C	B	A	F = ABCD + A'BCD + A'B'CD + A'B'C'D

			1
		1
		1	1
	1
	1		1
	1	1
	1	1	1
1				1
1			1
1		1
1		1	1
1	1			1
1	1		1
1	1	1		1
1	1	1	1	1

Perhaps the easiest way to generate the canonical form of a Boolean function is to first generate the truth table for that function and then build the canonical form from the truth table. In fact, we'll use this technique when converting between the two canonical forms.

8.5.2 Deriving the Sum of Minterms Canonical Form Algebraically

It is also a simple matter to generate the sum of minterms canonical form algebraically. Using the distributive law and theorem 15 ( A + A' = 1 ) makes this task easy. Consider F ₂₄₈ = AB + C . This function contains two terms, AB and C , but they are not minterms. We can convert the first term to a sum of minterms as follows:

 AB     =    AB * 1           By Th4         =    AB * (C + C')    By Th 15         =    ABC + ABC'       By distributive law         =    CBA + C'BA       By associative law

Similarly, we can convert the second term in F ₂₄₈ to a sum of minterms as follows:

 C      =    C * 1                            By Th4         =    C * (A +                         By Th15         =    CA + CA'                         By distributive law         =    CA * 1 +                         By Th4         =    CA * (B                          By Th15         =    CAB + CAB' + CA'B + CA'B'        By distributive law         =    CBA + CBA' + CB'A + CB'A'        By associative law

The last step (rearranging the terms) in these two conversions is optional. To obtain the final canonical form for F ₂₄₈ we need only sum the results from these two conversions:

 F ₂₄₈ = (CBA + C'BA) + (CBA + CBA' + CB'A + CB'A')       = CBA + CBA' + CB'A + CB'A' + C'BA

8.5.3 Product of Maxterms Canonical Form

Another canonical form is the products of maxterms . A maxterm is the sum (logical OR) of all input variables, primed or unprimed. For example, consider the following logic function G of three variables in products of maxterms form:

 G = (A + B + C) * (A' + B + C) * (A + B' + C)

Like the sum of minterms form, there is exactly one product of maxterms for each possible logic function. Of course, for every product of maxterms form, there is an equivalent sum of minterms form. In fact, the function G in this example is equivalent to the earlier sum of minterms form of F ₂₄₈ :

 F ₂₄₈ = CBA + CBA' + CB'A + CB'A' + C'BA = AB + C

Generating a truth table from the product of maxterms is no more difficult than building it from the sum of minterms. You use the duality principle to accomplish this. Remember, the duality principle says to swap AND for OR and zeros for ones (and vice versa). Therefore, to build the truth table, you would first swap primed and non-primed literals. In G , this would yield:

 G= (A' + B' + C') * (A + B' + C') * (A' + B + C')

The next step is to swap the logical OR and logical AND operators. This produces the following:

 G = A'B'C' + AB'C' + A'BC'

Finally, you need to swap all zeros and ones. This means that for each of the maxterms listed above, you need to store zeros into the function column of the truth table, and then fill in the rest of the truth table's function column with ones. This will place a zero in rows zero, one, and two in the truth table. Filling the remaining entries with ones produces F ₂₄₈ .

You can easily convert between these two canonical forms by generating the truth table for one form and working backward from the truth table to produce the other form. Consider the function of two variables, F ₇ = A + B . The sum of minterms form is F ₇ = A'B + AB' + AB . The truth table takes the form shown in Table 8-8.

Table 8-8: OR truth table for two variables
A	B	F ₇

1		1
	1	1
1	1	1

Working backward to get the product of maxterms, we first locate all entries in the truth table that have a zero result. The entry with A and B both equal to zero is the only entry with a zero result. This gives us the first step of G = A' B' . However, we still need to invert all the variables to obtain G = AB . By the duality principle, we also need to swap the logical OR and logical AND operators, obtaining G = A + B . This is the canonical product of maxterms form.