OPERATORS FOR MULTIDIMENSIONAL AGGREGATE DATA DEFINED IN A TABULAR ENVIRONMENT

The second approach mentioned above was created when some authors did not consider the relational model and its algebra as the correct data structure and the correct operator set for this kind of complex data. In fact, the relational model did not consider differences among columns, but it distinguished the difference between a column and a row. The latter is called a "tuple" of the relation, while all the columns were considered "attributes" of the relation, equivalent to each other. Previously, other authors highlighted the distinction between parameter (descriptive variable or category attribute) and measured data (quantitative variable or summary attribute), which becomes quite important in multidimensional aggregate databases, as observed in Johnson (1981), Shoshani (1982), Rafanelli & Ricci (1983), and Su (1983). Recently, because of the new application type, i.e., the On-Line Analytical Processing of data, different authors have proposed models which provide symmetric treatment not only of all dimensions, but also of measures, by considering a measure as another dimension. This fact brought about the definition of new operators (for example, push or pull), but also some considerations on the possibility to use the same set of operators after the exchange between the measure and one dimension, as we will see in the section relative to the OLAP environment.

The operators described in this section are able to operate on MAD, working only on the descriptive part of this data structure, with the automatic recomputation, if needed, of the measure (summary attribute). The recomputation of the new summary values depends on the type of summary data, i.e., on the aggregate function applied in the aggregation process to obtain the MAD. Moreover, this recomputation happens in a manner transparent to the user (automatic management of the summary type).

These operators have the aim of generating, from the set of tables memorized in the multidimensional aggregate database, those on which to carry out statistical analysis or On-Line Analytical Processing of data, which however turns out to be a subsequent phase tied to the use of statistical packages or similar ones. They present the following advantages:

1. flexibility and compactness in their use, in that they are independent from the single MAD and the single summary type (the control of the summary type is the responsibility of the user);

2. logical independence, in that the user does not have to specify the calculation procedures of the summary values and can therefore work on the metadata which describe the MAD by means of (possibly visual) interfaces, which use direct manipulation techniques, as proposed in Rafanelli (1990);

3. ease in verifying their properties (associative, commutative, etc.); in fact, it is not possible to set general conditions for the calculation procedures of the summary values and therefore verify the properties of the operators themselves.

It is important to underline the fact that no operator modifies the summary type of the measure, because to obtain this, it is necessary to use suitable statistical packages; in this case the user does not perform "data manipulation," but "data elaboration," even if, in the user activity, these two phases often intersect.

In Rafanelli & Ricci (1984, 1985), the authors proposed a statistical query language (STAQUEL) for the aggregate data definition and manipulation, and also the operators of summarization (which reduces the number of dimensions of a complex table by eliminating one or more category attributes) and of reclassification (which reduces the number of domain values related to category attributes by grouping them and, therefore, aggregating such groups). This reclassification is carried out along a predefined hierarchy, it is called (in OLAP applications) roll up.

In Fortunato et al. (1986), a distinction between operators independent of the summary type of a given table and operators dependent on this summary type is discussed. All these operators, for which that paper proposed a formal definition, are different from the traditional relational operators, because the data structure on which they work is different from a classical relation by being a more complex structure. In particular, as operators independent of summary type, they propose macro-union (on the same MAD schema, the union between the single pairs of equal attributes are performed), macro-select (single instances specified in a suitable table are selected), and comparison (two MAD or one MAD and one number are compared, according to a θ-operator (>, ≥, etc.), obtaining a new MAD with possible null values). As operators dependent on summary type, they propose summarization (one category attribute is deleted and the measure instances are recomputed), restriction (only the category attributes specified by a qualification condition are selected for the new MAD), enlargement (practically the inverse of restriction, obtained by a distribution law expressed by a table), and reclassification (it substitutes a set of category attributes with another set, according to a functional dependency expressed by a relation).

The Mefisto model, based on the previous aggregate data structure and on a reviewed set of operators, has been proposed in Rafanelli & Ricci (1988, 1990, 1991, 1993). In these papers a formalization of the above-mentioned elements of the model (data structure and operators) is illustrated. Part of these operators were further studied in later papers (see Rafanelli & Shoshani, 1990; Bezenchek, Rafanelli, & Tininini, 1996a, 1996b).

As mentioned in the introduction of this chapter, visualization and data analysis (which represent, together with query formulation and extracting aggregate data from a database, the four steps for data analysis applications, as discussed in Gray et al., 1997), use tools which carry out dimensionality reduction (aggregation or summarization) in order to represent the dataset as an n-dimensional space. Boolean operations or logical associations between data are not of prime importance to users; in addition, updating and deleting data is rare or forbidden (see Ghosh, 1986), because their statistical use means they are generally considered static data, that is, data which represent "events consolidated in time." In fact, the most common manipulation is related to the encoding of data summarization, or to the reclassification of the descriptive data. In order to schematically represent the operations formally described later in this chapter, we use the graph in Figure 1, where the orientated edges go from the input data structure to the output data structure, with regard to the operations associated with a single edge.

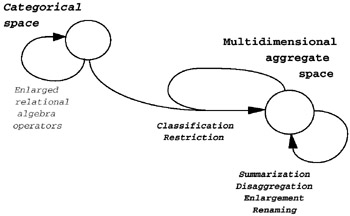
Figure 1

The algebra operations can have one or two multidimensional aggregate entities in input, or the couple <relation, multidimensional aggregate entity>; output is one multidimensional aggregate entity. The relational algebra operations (see, for example, Abiteboul, Hull, & Vianu, 1995) are necessary for the manipulation of relations resulting from the performance of the comparison operation; they are relations in non-first normal-form (that is, relations having a set like tuple components, relations such as those discussed in Ozsoyoglu, Ozsoyoglu, & Matos (1987).

The operators, described in the following, refer to the n-dimensional aggregate data structure, generally represented by a table. They are able to operate on this data structure, working only on its descriptive part. Furthermore the way of working on the summary values is included in each operation, that is, the computation of the summary values is automatic and therefore it happens in a manner transparent to the user.