5.2 CRYPTOGRAPHIC HASH FUNCTIONS

Team-Fly

According to [3], a hash function is a function h that has, as a minimum, the following two properties:

h maps an input x of arbitrary finite bit-length, to an output h(x) of fixed bit-length (compression);
Given h and x, h(x) is easy to compute (ease of computation).

In addition, hash functions that are relevant for cryptographic applications (i.e., cryptographic hash functions) may fulfill one or several of the following requirements [3]:

A hash function is preimage resistant (or one-way) if for essentially all prespecified outputs, it is computationally infeasible to find any input which hashes to that output, that is, to find any preimage x′ such that h(x′) = y when given any y for which a corresponding input is not known.
A hash function is second-preimage resistant (or weak collision resistant) if it is computationally infeasible to find any second input which has the same output as any specified input, that is, given x, to find a second preimage x′ ≠ x such that h(x) = h(x′).
A hash function is collision resistant (or strong collision resistant) if it is computationally infeasible to find any distinct inputs x, x' that has the same output, that is, such that h(x) = h(x′).

In the literature, the term one-way hash function (OWHF) or weak one-way hash function is often used to refer to a hash function that is both preimage resistant and second-preimage resistant, whereas the term collision resistant hash function (CRHF) or strong one-way hash function is often used to refer to a hash function that is collision resistant. Furthermore, the term cryptographic hash function is used to refer to either of them (i.e., OWHF or CRHF). Mainly because of their efficiency, cryptographic hash functions are of central importance for cryptographic algorithms and protocols. For example, OWHFs can be used to compute and verify digests for arbitrary messages. In this context, OWHFs may also be called message digest algorithms, and in this book we use both terms synonymously and interchangeably.

All definitions given above are not precise in a mathematically strong sense, because they do not resolve what the terms "easy" and "computationally infeasible" actually mean. Nevertheless, we want to use these definitions in this book. It is important to note that the existence of OWHF (or even CRHF) is still an unproven assumption and that, until today, no function has been shown to be preimage resistant (i.e., one-way) in a mathematically pure sense. Obviously, a sufficiently large domain prohibiting an exhaustive search is a necessary but not sufficient condition for a function to be preimage resistant.

Most cryptographic hash functions in use today are iterative. In short, a cryptographic hash function is iterative if data are hashed by iterating a basic compression function on subsequent blocks of data. The basic idea is illustrated in Figure 5.1. A message x is decomposed into n blocks of data x₁, …, x_n. A basic compression function f is then applied to each block and the result of the compression function of the previous block. This continues until the result of the last compression step is interpreted as output h(x). Examples of such cryptographic hash functions include MD2 [9], MD4 [10], MD5 [11], and the secure hash algorithm 1 (SHA-1) [12]. MD2, MD4, and MD5 produce 128-bit hash values, whereas SHA-1 produces 160-bit hash values. RIPEMD is another example of an iterative cryptographic hash function. It was developed as part of a European research project and is basically a variation of MD4. RIPEMD-160 is a strengthened version of RIPEMD producing another 160-bit hash value [13].

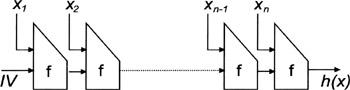
click to expand
Figure 5.1: An iterative cryptographic hash function

As of this writing, MD5 and SHA-1 are by far the most widely used and deployed cryptographic hash functions. MD5 takes as input a string of arbitrary length and produces as output a 128-bit hash value. In theory, we would need 2¹²⁸ (in the worst case) or 2¹²⁷ (in the average case) trials before finding a preimage, and hence a new message that results in the same MD5 hash value. Even if each trial only lasted a nanosecond, this would still require some billions of billions of centuries in computing time. However, recent results in cryptographic research show that it is possible to take advantage of the particularities of the cryptographic hash function algorithm to speed up the search process. According to Paul van Oorschot and Michael Wiener, you can actually build a machine able to find messages that hash to an arbitrary value [14]. What this means is that cryptanalysis is catching up and that a 128-bit hash value may soon be insufficient. In addition, Hans Dobbertin has shown that MD5 is vulnerable to specific collision search attacks [15]. Taking this into account, SHA-1 and RIPEMD-160 appear to be a cryptographically stronger cryptographic hash function than MD5. In any case, implementors and users of cryptographic hash functions should be aware of possible cryptanalytic developments regarding any of these functions, and the eventual need to replace them.

Team-Fly