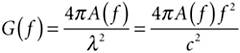Section 2.3. UWB Antennas

2.3. UWB Antennas^[1]

^[1] Section 2.3 courtesy of Dr. Hans Schantz. Portions reprinted with permission from "Introduction to Ultra-Wideband Antennas," in 2003 IEEE Conference on Ultra Wideband Systems and Technologies. © 2003 IEEE.

An antenna is a transducer that converts guided electromagnetic energy in a transmission line to radiated electromagnetic energy in free space. Antennas also can be viewed as impedance transformers, coupling between an input or line impedance and the impedance of free space.

The imminent widespread commercial deployment of UWB systems has sparked renewed interest in the subject of ultra-wideband antennas. The power levels authorized by the FCC mean that every decibel counts in a UWB systemas much as or perhaps even more than in a standard narrowband system. Thus, an effective UWB antenna is a critical part of an overall UWB system design.

UWB antennas have been in active commercial use for decades. In a sense, even the venerable AM broadcast band antenna is "UWB" since it covers a band from 535 KHz to 1705 KHz for a fractional bandwidth in excess of 100 percent. Because a high-quality broadcast AM antenna is really a tuned antenna designed to pick up an individual narrowband (10 KHz) channel, the effective fractional bandwidth is really only 0.6 to 1.9 percent, and only one channel can be received at a time.

This is a particularly stark example, but it highlights the difficulty with traditional UWB antennas: they are typically "multi-narrowband" antennas instead of antennas optimized to receive a single coherent signal across their entire operating bandwidth. Some modulation schemes are more tolerant of antenna variations than others. For instance, a multiband or OFDM approach may be less vulnerable to dispersion or other variations across an antenna's operational band. Nevertheless, a UWB system requires an antenna capable of receiving on all frequencies at the same time. Thus, antenna behavior and performance must be consistent and predictable across the entire band. Ideally, pattern and matching should be stable across the entire band.

In addition, a UWB antenna is preferentially nondispersive, having a fixed phase center. If waveform dispersion occurs in a predictable fashion, it may be possible to compensate for it, but in general it is desirable to radiate similar waveforms in all directions. A log-periodic antenna is an example of a dispersive antenna. Larger scale components radiate low-frequency components, while smaller scale components radiate high-frequency components. The result is a chirplike, dispersive waveform. Worse, the waveform will vary at different azimuthal angles around the antenna. Again, a multiband or OFDM approach may be more tolerant of dispersive antennas.

By contrast, a small-element antenna, such as a planar elliptical dipole, tends to radiate a more compact, nondispersive waveform, similar to a "Gaussian W." This behavior is illustrated in Figure 2-5. A small-element antenna tends to be not only nondispersive but also more compact. Hence, these antennas are preferred in many applications.

Figure 2-5. (a) A log-periodic antenna (left) has a dispersive waveform (right). (b) An elliptical dipole (left) has a nondispersive waveform (right).

The aim of this section is to provide an overview of and an introduction to UWB antennas. The next subsectionexplains key UWB antenna concepts and discusses system and network considerations for UWB antennas.

2.3.1. UWB Antenna Concepts

A wide variety of antennas are suitable for use in ultra-wideband applications. Some of these are described elsewhere in a historical survey [9]. UWB antennas may be classified as directional or nondirectional. They may further be classified as either electric or magnetic antennas. These classifications as well as the various types of UWB antennas will be considered in turn.

Directionality of Antennas

High-gain or directional antennas concentrate energy into a narrower solid angle than omnidirectional antennas. An isotropic antenna has a gain of 0 dBi by definition (such an antenna is not physically realizable, at least not in terms of instantaneous pattern). In fact, dBi means "decibels relative to an ideal isotropic antenna." A typical dipole antenna has a gain of about 2.2 dBi. High-gain horn or reflector antennas may have gains of +10 dBi, +20 dBi, or even more, as shown in Figure 2-6. Antenna efficiency is included in the definition of antenna gain, so a 50 percent efficient (3 dB) dipole will have a gain of about 1.8 dBi.

Figure 2-6. (a) An isotropic antenna has a gain of 0 dBi by definition, (b) a small dipole antenna typically has a gain of about 2.2 dBi, and (c) a horn antenna may have a gain of 10 dBi or more.

As shown in Figure 2-6, a directional antenna has high gain, it has a narrow field of view, and it is relatively large in size. An omnidirectional antenna has relatively low gain, it has a wide field of view, and it tends to be relatively small. The fundamental trade-offs with directional antennas are shown in Table 2-1.

Table 2-1. Trade-offs between directional and omnidirectional antennas

	Directional	Omnidirectional
Gain	High	Low
Field of View	Narrow	Wide
Antenna Size	Large	Small

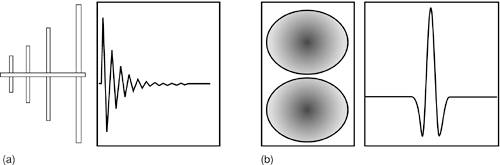
Note that regulatory constraints require transmit power to be decreased when using a high-gain directional transmit antenna so as to meet the same peak radiated emission limit. Thus, a high-gain transmit antenna does not add directly to the link budget except insofar as it might reduce emissions in undesired directions. This can potentially reduce clutter and enhance overall system performance or capacity. Of course, a high-gain receive antenna adds directly to link performance and is always desirable where the relatively larger size and narrower field of view can be tolerated. These trade-offs are illustrated in Figure 2-7.

Figure 2-7. (a) A low-gain, omnidirectional antenna may be replaced by (b) a high-gain directional antenna, but transmit power must be reduced to meet the same regulatory limit for peak power. Also, a high-gain antenna will tend to be larger and have a narrower field of view than a low-gain omnidirectional one.

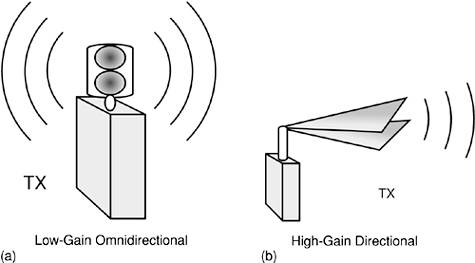
Implications of antenna directivity and gain for overall system performance are discussed in Section 2.3.2.

Electric or Magnetic Antennas

Antennas also can be classified as either electric or magnetic. Electric antennas include dipoles and most horns. These antennas are characterized by intense electric fields close to the antenna. Magnetic antennas include loops and slots and are characterized by intense magnetic fields close to the antenna [10].

Electric antennas are more prone to couple to nearby objects than magnetic antennas. Thus, magnetic antennas are preferred for applications involving embedded antennas.

Types of Antennas

Many specific kinds of UWB antennas fall within these general categories. Directional antennas include horn and reflector antennas. These antennas can also be implemented in relatively compact planar designs. Small-element antennas, such as dipoles or loops, are preferred for omnidirectional coverage or where space is at a particular premium. Traditional "frequency independent" antennas, such as log periodics or spiral antennas, tend to be larger and can be used only if waveform dispersion across the field of view can be tolerated. UWB antennas can also be combined in arrays [11, 12].

2.3.2. System and Network Considerations for UWB Antennas

Traditional narrowband concepts and techniques often require revision in order to be applied in the UWB context. This section discusses first the problem of antenna matching and then the relationship between directivity and system performance.

Matching and Spectral Control in UWB Systems

Traditionally, a narrowband antenna is treated as a black box with given fixed properties. A system designer either accepts the penalties imposed by an antenna's shortcomings or designs a matching network to bridge any impedance gap between the RF front end and the antenna.

A clever matching network can conceal a wealth of antenna sins in the narrowband context. Such matching networks become increasingly difficult to construct as the bandwidth increases. In the UWB context, a good impedance match to an antenna must be designed in from first principles, not added as an afterthought.

The concept of specifically designing an antenna to have a particular impedance has been understood for some time. For instance, Nester disclosed a planar horn antenna with continuously variable elements [13]. This antenna transitions smoothly from a microstrip to a slotline architecture while maintaining an impedance match. Nester's antenna design is shown in Figure 2-8.

Figure 2-8. The continuously tapered slot horn elements of Nester (gray colorization on elements added). A detailed description of this antenna, as well as explanations of each marking on the figure, are available in U.S. Patent 4,500,887 [13].

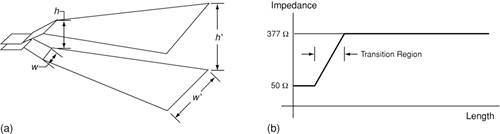
Calculating the impedance of a slotline horn requires some complicated algorithms [14]. For simplicity in discussion, assume a parallel plate horn antenna with a cross-sectional width w and a height h. Then the impedance of an air gap horn is given approximately by:

Equation 2-1

Note that this result is only exact for w >> ~10 h values. Since the free space impedance is Z₀ = 377 , a 50 match requires w ~ 7.54, while a 377 match requires w ~ 1.00.

Consider a hypothetical horn antenna matched to 50 at its feed, with a linear transition from 50 to , and a long section tapered to be responsive to an ultra-wideband of frequencies. The format of this antenna is shown in Figure 2-9.

Figure 2-9. (a) A hypothetical tapered horn antenna, with (b) a transition from 50 to

Just as a desired impedance can be designed into an antenna, so can a desired frequency range. The simplest example of this kind of manipulation is to vary the scale of an antenna. For instance, planar elliptical dipoles offer a reflection coefficient, S₁₁, on the order of 20 dB across a 3:1 frequency range [15]. The minor axis is approximately 0.14 l at the lower end of the operating band. Thus, a 13 GHz antenna will have approximately 1.67-inch elements, a 26 GHz antenna will be half the size (one-fourth the area) with about 0.83-inch elements, and a 39 GHz antenna will be one-third the size (one-ninth the area) with approximately 0.56-inch elements. The antenna size can be scaled to select any particular 3:1 range of desired frequencies. The designs of these antennas are shown in Figure 2-10.

Figure 2-10. A family of planar elliptical dipole antennas responsive to various frequency ranges. Element size is shown in inches.

However, this is really just the first step in specifically tailoring an antenna's spectral response to fit a particular design goal. Frequency notches can be implemented using more sophisticated techniques, thus making an antenna insensitive to particular frequencies [16]. Also, the rate of spectral roll-off at the edges of an antenna's operational band can be controlled to some extent [17].

While traditional narrowband system design can afford to take a laissez-faire attitude toward antennas, pounding a square-peg antenna into a round-hole RF front end using a matching-network hammer, an ultra-wideband system design requires a more holistic approach. A UWB antenna must be specifically tailored in both impedance and spectral response to contribute to the overall system performance.

The concept of using an antenna as a spectral filter is not entirely novel. In spark gap days, RF engineers excited resonant antennas with low- frequency broadband impulses, counting on the antenna response to select and radiate the correct frequency components. As we revisit and build on their pioneering work, we must similarly take advantage of antenna properties to meet system goals.

Directivity and System Performance

As with narrowband antennas, the link behavior of UWB antennas in free space is governed by Friis's Law:

Equation 2-2

where P_RX is the received power, P_TX is the transmitted power, G_TX is the transmit antenna gain, G_RX is the receive antenna gain, l is the wavelength, f is the frequency, c is the speed of light, and r is the range between the antennas.

Friis's Law depends on frequency because, in general, power and gain will be functions of frequency [18]. Thus, in the ultra-wideband case, Friis's Law must be interpreted in terms of spectral power density such as:

Equation 2-3

One must integrate over frequency to find the total received power:

Equation 2-4

and the effective isotropic radiated power (EIRP) is

Equation 2-5

where G_TX(f) must be the peak gain of the antenna in any orientation. Because regulatory limits are defined in terms of EIRP, a system designer aims for the product P_TX(f) G_TX(f) to be constant and as close to the regulatory limit as a reasonable margin of safety (typically 3 dB) will allow.

Similarly, this power gain product must roll off so as to fall within the skirts of the allowed spectral mask. Thus, both the antenna designer and the transmitter designer must work together to achieve a desired P_TX(f)G_TX(f), and shortcomings in one spectral response can be made up for and compensated in the other. Note the dependence of the received power on the inverse frequency squared. Colloquially, this (l/4pr)² or (c/4prf)² variation of the signal power is called "path loss." This makes sense (in a way) because the greater the range r, the larger the 4pr² surface area over which a signal is spread, and thus the weaker the captured signal. This is more a diffusion of the signal energy than a loss. Further confusion enters in considering the frequency dependence of path loss. Interpreting this 1/f² dependence as a part of path loss suggests that somehow free space attenuates signals in a manner inversely proportional to the square of the frequency. Of course, this is not the case. The 1/f² dependence enters because of the definitions of antenna gain and antenna aperture. Antenna gain G is defined in terms of antenna aperture A as:

Equation 2-6

This antenna aperture is the effective area of the antenna: a measure of how big a piece of an incoming wavefront an antenna can intercept. For directive, electrically large antennas, antenna aperture tends to be comparable to the physical area. For omnidirectional small-element antennas, the antenna aperture may actually be significantly larger than the antenna's physical area. This follows from the ability of electromagnetic waves to couple to objects within about l/2p. Thus, even though a thin wire or planar antenna may have negligible cross-sectional area, it can still be an effective receiver or radiator of electromagnetic radiation.

The aperture of a constant-gain antenna remains constant in units of wavelength. For instance, a dipole antenna has an aperture of approximately 132l². As frequency f increases, l decreases, and the constant-gain antenna aperture rolls off as 1/f². Typically an omnidirectional antenna is designed so as to have constant gain and pattern, and thus an omni-directional antenna exhibits this behavior.

Conversely, a constant-aperture antenna is one whose antenna aperture remains fixed with frequency. For instance, a horn antenna will typically (but not always) have a fixed aperture. As frequency f increases, the size of this aperture in units of wavelength increases as f². This narrows the pattern and increases the antenna gain as f². Many (but not all) directive antennas exhibit this behavior. Figure 2-11 shows the pattern behavior of omni versus directional antennas.

Figure 2-11. The pattern of a constant-gain antenna remains fixed with increasing frequency (top), while the pattern of a constant-aperture antenna narrows and gain increases with increasing frequency (bottom).

In an omni-to-omni link, the constant-gain antennas on both sides of the link result in the received power rolling off as 1/f² in band. A constant-aperture receive antenna whose gain varies as f² cancels out this 1/f² roll-off and yields a flat received power in band. This received power may be significantly greater than that of a comparable omni antenna depending on the magnitude of the receive antenna gain. This advantage is offset by a narrowing of the pattern and field of view that accompanies the increasing gain of a typical directional antenna. Using a directional antenna whose gain varies as f² on the transmit side of the link does not improve matters further, because the transmit power must be made to roll off as 1/f² to meet the same flat EIRP spectral mask. Figure 2-12 depicts this behavior.

Figure 2-12. The relationship between antenna directivity and link performance for (a) an omni TX to an omni RX, (b) an omni TX to a directional RX, and (c) a directional TX to a directional RX

A final potential advantage of directive antennas relative to omnidirectional antennas is their ability to isolate signals arriving in particular directions. This ability can be useful in determining the angle of arrival of signals, in applying spatial processing techniques to incoming multipath signal components, and in nulling out undesired interfering signals.

This discussion implicitly assumed a single broadband signal occupying the entire bandwidth. However, the general conclusions remain valid for a multiband or OFDM type implementation. In a multiband implementation, a designer still seeks to have coded, multiband, or hopping signals yield an average effective power spectrum comparable to that of a broadband impulse implementation.

A finite difference time domain (FDTD)^[2] analysis helps in understanding the detailed physics of how signals evolve from a transmit signal via a radiated signal to a received signal. A more detailed physical analysis of radiated and received signals from a typical UWB antenna is available in [19].

^[2] Finite difference time domain is a well-known electromagnetic modeling technique. This method enables precise characterization of complex structures for which analytical methods are not suitable. For more information on FDTD, refer to [2].