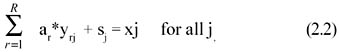BASIC COST MODELS AND ESTIMATION MODELS

Chapter X - Maximum Performance Efficiency Approaches for Estimating Best Practice Costs
Data Mining: Opportunities and Challenges
by John Wang (ed)
Idea Group Publishing 2003

	Brought to you by Team-Fly

There are two uses of the word "model" in this chapter. By the basic cost model, we mean the assumed relationship between the cost driver of an activity and its contribution to the total cost pool. The simplest case is that of proportional variation. Let yr be the amount of the r-th cost driver. Under the basic cost model, the contribution to the total cost pool will be a_ry_r, where a_r may be called the average cost per unit of y_r or simply the cost rate. This chapter focuses on this basic cost model. Some other models such as for estimating marginal costs are discussed briefly. The other use of the word "model" refers to the method used to solve for estimates of the basic cost model parameters the a*_r. The estimation models used here are LP models. As noted above, this usage of LP does not appear to be similar to previous uses in the accounting literature, but is a consequence of the estimation principle used.

Suppose there are r=1 R_r activities with associated cost driver quantities of y_r, respectively. Then, as in Cooper and Kaplan (1992), the cost of resources consumed is given by ∑a_ry_r. If x is the actual total cost pool associated with these activities, the cost of resources supplied, then there may be a difference, s ≥ 0, such that

Cooper and Kaplan (1992) call s the cost of unused capacity. In their analysis, the x value was a budget figure and the y_r could vary due to decreased demands. We start from the same construct but regard variations of the y_r and x as due to more or less efficiency. By defining what may be called best practice a_r values, we therefore associate the s value with possible inefficiency of a business unit, a cost of inefficiency.

Thus suppose we have j = 1 N comparable business units, achieving y_rj units of driver r, respectively, and with associated cost pools, x_j. In addition to having the same activities and cost drivers, we further require that comparable units be similar in the sense that the practices, policies, technologies, employee competence levels, and managerial actions of any one should be transferable, in principle, to any other. Define a_r* as the vector of cost rates associated with the most efficient unit or units under comparison. Then in the equation

the cost of unused capacity, s_j, may be interpreted as an inefficiency suffered by a failure to achieve larger y_rj values, smaller x_j value, or some combination of these. The ratio v_j = ∑ a_r*y_rj/ xj, is an efficiency measure for the j-th unit when the a_r* are the true benchmark cost rates and ∑ a_r*y_rj≤x_j holds for all units. A technique for estimating parameters in efficiency ratios of the above form was proposed in Troutt (1995). In that paper, the primary data were specific decisions. Here a more general form of that approach called maximum performance efficiency (MPE) is proposed and applied to estimate the benchmark a_r* values. Assume that each unit j = 1 N, seeks to achieve maximum (1.0) efficiency. Then the whole set of units may be regarded as attempting to maximize the sum of these efficiency ratios, namely, ∑∑a_r*y_rj/ x_j. The maximum performance efficiency estimation principle proposes estimates of the a_r* as those which render the total, or equivalently the average, of these efficiencies a maximum.

Maximum Performance Efficiency (MPE) Estimation Principle: In a performance model depending on an unknown parameter vector, select as the estimate of the parameter vector that value for which the total performance is greatest.

Use of the word performance is stressed in the MPE name to emphasize the more general utility of the approach than was indicated by the earlier MDE term. Managerial performance, such as in the units under study here, involves many kinds, levels, and horizons of decisions.

Define the data elements Y_rj by Y_rj = y_rj/x_j. Then the MPE estimation criterion for the benchmark a_r* values is given by

Problem MPE is a linear programming problem. Its unknown variables are the best practice cost rates, the a_r* values. Solution of this model provides values for the a_r* as well as the unit efficiencies, v_j. A model adequacy or validation approach for this estimation procedure is proposed in a later section. As a linear programming problem, the MPE model is readily solved by a wide variety of commonly available software products. MPE may be seen here to be an estimation criterion analogous to the ordinary least squares error criterion in regression. The cost model, ∑ a_r Y_rj is analogous to the regression model.

	Brought to you by Team-Fly