Hash Algorithms
| As we shall see, cryptographic hash functions are used in digital signatures, since they can be efficiently used for detecting message tampering. A hash is a function that maps an arbitrary-length binary data input to a small, fixed-length binary data output, often referred to as a message digest or finger print . Good Hash Function CharacteristicsA good hash function should have the property that it is a very low probability that two distinct inputs collide, producing the same hash value result. This allows the smaller, more manageable hash to be used effectively to represent or identify the larger data object. This is analogous to using a human fingerprint , which is a small and manageable, yet highly characteristic piece of information that can be used to identify or authenticate its owner. The fact that for any particular hash value, it is exceedingly difficult to find another distinct input message that would produce the same hash output is precisely what protects a digitally signed message from being tampered with. [1]
Simple hash functions have many uses in computing outside of the specialized discipline of cryptography, such as for error detection and quickly searching for objects in a hash table. The GetHashCode virtual method of Object is an example of a simple hash function not intended for cryptographic purposes. How does a cryptographic hash function differ from an ordinary hash function such as GetHashCode ? A cryptographic hash function is a hash function with some additional characteristics that are required for cryptographic purposes, such as password hashing or digital signing. For example, for a cryptographic hash function, it should be infeasible to compute a valid input data from knowing only the output hash value. It should also be infeasible, given one input data, to discover an alternate input data that would produce the same hash value. Additionally, it is also highly desirable that a hash function be efficient to compute. There is a clear tradeoff here, since achieving greater security comes at the expense of a penalty in performance. Fortunately, MD5, SHA-1, as well as SHA-256, SHA-384, and SHA-512 are all quite efficient designs that provide choice and balance in their security/performance tradeoff . Of these, MD5 is the fastest , but, of course, it is also the least secure. It is also desirable that a small number of bit changes on the input data should produce a large number of unpredictable bit changes in the resulting output hash value. This makes it more difficult to reverse-engineer the input from the output. In summary, an ideal cryptographic hash function has the following properties:
The last point mentioned means that it is hard to find two distinct inputs that produce the same output. This may seem odd at first glance. If you can have input data that is of any arbitrary length, then there are an infinite number of possible inputs. If the hash output has a fixed size, then there are only a finite number of possible outputs. Thus, it is obvious that there must be an infinite number of inputs that do in fact produce a collision of identical outputs. It may seem paradoxical, however, that even though there are an infinite number of colliding inputs for any given output, it is still extraordinarily difficult to find even just two such colliding inputs! Thus, the fact that collisions are hard to find is not due to the fact that few collisions exist, since there are many. Rather, collisions are hard to find because such collisions are interspersed with a very much larger number of message pairs that do not collide. The security of the hash results from the extreme difficulty in finding any of these infinitely numbered colliding input pairs! Hash Algorithms Provided by .NETThe two most commonly used cryptographic hash functions are SHA-1 (Secure Hash Algorithm published by NIST in the mid 1990s) and MD5 (Message Digest algorithm designed by R. Rivest in the early 1990s). In addition, several important new versions of SHA have recently been published. Keyed hash algorithms are also important for certain message authentication “ related purposes. These are all supported by the .NET Framework in the form of the classes derived from HashAlgorithm : [2]
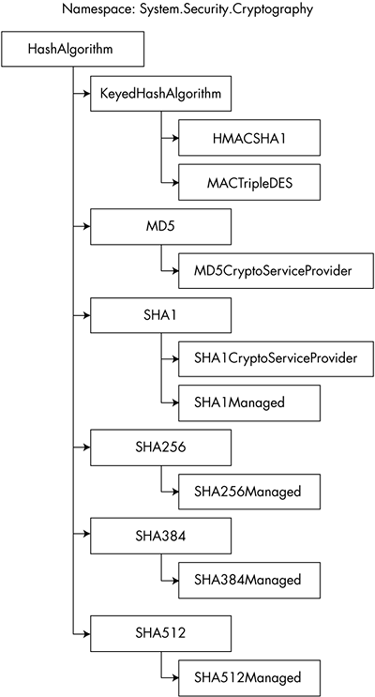
Figure 5-1 shows the hash algorithm class hierarchy. The Object -derived abstract class HashAlgorithm sits at the top of this hierarchy. The derived abstract classes KeyedHashAlgorithm, MD5, SHA1, SHA256, SHA384 , and SHA512 represent each of the most commonly used cryptographic hash algorithms in use today. Since these are all abstract classes, they cannot be instantiated or directly used. Derived from each of these are the concrete implementation classes that can be directly used. Those class names that end in the word CryptoServiceProvider are implemented using the underlying unmanaged CryptoAPI functionality provided by the operating system. Those that end with the word Managed are implemented entirely from scratch in managed C# code, independently of the CryptoAPI. Figure 5-1. The hash algorithm hierarchy. The HMACSHA1 class produces a keyed hash (Keyed-Hash Message Authentication Code, or HMAC) using the SHA-1 hash function. The MACTripleDES class produces a keyed hash HMAC using Triple DES [3] encryption as a hash function. An HMAC is similar to a digital signature in that it can be used to verify message authenticity and integrity; however, it differs in that it is not suitable for enforcing nonrepudiation: Whereas a digital signature is an asymmetric scheme in which one key is held private, an HMAC is a symmetric scheme in which both the sender and receiver use the same secret key for applying and verifying the MAC. Since the key is known by more than one individual, there is no way to prove to a third party which of those individuals applied the hash. Also, MACs are smaller and more efficient to compute than digital signatures.
Although the .NET framework is very extensible, allowing proprietary hash algorithms to be implemented as classes derived from HashAlgorithm , it is highly recommended that you do not attempt to design your own cryptographic algorithms! To be considered secure, a cryptographic algorithm must be analyzed intensively by many experts in the field over a prolonged period. It is a widely held opinion that any gains in security that may result from the obscurity of a proprietary design is far outweighed by the likelihood that such a design is dangerously flawed. Rather, it is much better to use an existing trusted algorithm such as MD5 or one of the SHA variants. Beyond those supported by .NET, there are no other cryptographic hash algorithms that are currently in significant use in the industry. [4] The underlying Microsoft Windows CryptoAPI and CSP (cryptographic service provider) support three hash algorithms: MD4, MD5, and SHA-1. The .NET Framework does not support MD4, since MD5 is an improvement over MD4, which has critical weaknesses that have been fixed. The .NET Framework does support SHA-256, SHA-384, and SHA-512, which are not supported by the underlying CryptoAPI, since these are relatively new standards.
The HashAlgorithm ClassThe HashAlgorithm class has a public property named Hash , which is a byte array containing the resulting hash value. The public property HashSize gets the size of the hash code in bits. The most important public method of the HashAlgorithm class is ComputeHash , which returns the hash value as a byte array for the input data provided as a byte array parameter. The following code shows how the HashAlgorithm class is used, along with the concrete derived class that encapsulates the SHA-1 algorithm. This example assumes that the input message messageByteArray has been previously instantiated as a byte array. HashAlgorithm sha1 = new SHA1CryptoServiceProvider (); byte[] sha1Hash = sha1. ComputeHash (messageByteArray); The MD5 and SHA ClassesThe MD5 class encapsulates the MD5 algorithm, which takes an input of arbitrary length and produces a 128-bit hash result. The MD5 message digest algorithm is defined in RFC 1321. [5] This algorithm was originally designed for digital signature applications, where the hash (i.e., message digest) is encrypted with a private key in the RSA public key cryptosystem. The MD5 algorithm is an extension of the MD4 message digest algorithm (published by Rivest in 1990), but, while slightly slower, it provides more security.
The SHA1 class encapsulates the SHA-1 algorithm. SHA-1 can take any message up to 2 64 bits in length and produce a 160-bit hash output. This message digest can be fed into the DSA, [6] as we shall see shortly. The SHA-1 algorithm has been adopted as the NIST standard known as the SHS (Secure Hash Standard), which is published in FIPS PUB 180-1. [7] It is interesting to note that the FIPS 180-1 document states that SHA-1 is based on principles similar to those used in the design of the MD4 message digest algorithm. Therefore, the two most heavily used hash functions, MD5 and SHA-1, are related to one another.
The SHA256, SHA384 , and SHA512 classes encapsulate a closely related set of hash algorithms, which produce hash sizes of 256, 384, and 512 bits. These new algorithms, defined in FIPS PUB 180-2 [8] in 2002, are closely related to SHA-1, but, since the original publication of FIPS PUB 180-1 in 1993, concerns have been raised over whether 160 bits provide sufficient security for highly sensitive applications over the long term . Whereas a brute-force attack on an n -bit symmetric encryption algorithm represents a work factor that is proportional to 2 n , an attack on an n -bit cryptographic hash algorithm is only2 n /2 . This is because a birthday attack [9] on the hash is considered successful if any two inputs are found that produce the same hash output. Therefore, the work factor for attacking the 160-bit SHA-1 algorithm is actually only on the order of 2 80 . This is still probably beyond the reach of almost all existing adversaries, but probably not sufficient for extremely high security requirements over the very long term.
It is interesting to note that the newly selected AES symmetric encryption standard, known as Rijndael, comes in three flavors based on key size: AES-128, AES-192, and AES-256. You may notice that the bit sizes of the new SHA algorithms are 256, 384, and 512, which are exactly double that of the corresponding 128, 192, and 256 bit sizes for AES. This effectively makes the new AES and SHA algorithms of equivalent strength, since a hash is vulnerable to a birthday attack, which cuts the work factor by two. This is an important point if you are constructing a security protocol that involves both symmetric encryption and secure hashing. This is because the security of the entire protocol is only as strong as the weakest link. For example, if you use a very high-security symmetric algorithm, and combine that with a relatively weak hash algorithm (or vice versa), then your adversary will simply attack the weaker of the two. In effect, you will have wasted processing power and performance for zero gain in overall security. In contrast, if you combine algorithms of equivalent strength, then all processing overhead effectively contributes equally towards the desired level of security. The KeyedHashAlgorithm ClassThe KeyedHashAlgorithm class is an interesting variation on the basic hash algorithm concept in that it calculates a hash output that is based on both the message data fed into it as well as an additional piece of information used as a key input. Such a keyed hash algorithm is therefore a key-dependent, one-way hash function. This is handy for message authentication purposes, since only someone who knows the correct key can apply or verify the hash. Keyed hash algorithms therefore provide both integrity and authenticity checking between trusting parties that have exchanged key information. The KeyedHashAlgorithm class is abstract, which is implemented by the concrete derived HMACSHA1 and MACTripleDES classes, These classes encapsulate keyed hash algorithms based on the SHA-1 and Triple DES algorithms respectively. Object IdentifiersSometimes, programmers need a systematic naming convention that allows each of the hundreds of standard and proprietary protocols, algorithms, and data formats to be efficiently and uniquely identified. ASN.1 [10] OIDs (Object Identifiers) are defined and managed by a number of organizations, including ANSI (American National Standards Institute), for the purpose of uniquely identifying computing formats in a logical and hierarchical manner. There are a large number of OIDs that identify specific protocols, algorithms, and data formats. In particular, most encryption algorithms that are recognized by ANSI have also been assigned a unique OID. For example, the OIDs for the most commonly used cryptographic hash algorithms are shown in Table 5-1. We shall see that these OIDs must be specified in certain .NET Security Framework class methods , such as the SignHash and VerifyHash methods of the RSACryptoServiceProvider and DSACryptoServiceProvider classes.
Table 5-1. ASN.1 OIDs for Commonly Used Cryptographic Hash Algorithms
The following code snippet shows an example of using an OID as a parameter to the SignHash method of the RSACryptoServiceProvider class. Of course, it is assumed that the hashbytes variable is a byte array that has already been created by calling the ComputeHash method of the SHA1 class. //create RSA object using default key RSACryptoServiceProvider rsa = new RSACryptoServiceProvider(); //sign hash using OID for SHA-1 signaturebytes = rsa.SignHash(hashbytes, "1.3.14.3.2.26"); |
EAN: 2147483647
Pages: 126