3.9 Right Triangles and Angles

3.9 Right Triangles and Angles

Each triangle-right angled or not-has an angle sum of two right angles. In degrees, this is a total of 180. In a right triangle, one angle is a right angle, which measures 90 degrees. The other two angles in a right triangle are both acute angles and are also complementary angles because their sum is a right angle. In other words, together the three angles equal 180 degrees. The single largest angle in a right triangle-the right angle-is opposite the longest side, which is a diagonal called the hypotenuse. The other sides are named in relation to the other two acute angles. For angle θ, the side opposite the angle is called the opposite side, and the other is the adjacent side. However, for angle the names change around because a different side is opposite the angle-so the side opposite this angle becomes the new opposite, and the other side becomes the adjacent.

3.9.1 Sides, Angles, and Ratios

Given two right triangles it can immediately be established that each triangle has a single right angle. This is the angle opposite the hypotenuse. Additionally, the triangle also has two acute complementary angles whose sum is also a right angle. It follows, therefore, that if one of the acute angles is known, the other angle is also known. For example, if θ is 30 degrees, then the other angle must be 90−30 = 60.

If two right triangles have the same angles, the two triangles are said to be similar, and this means the length of their sides will be proportional. That is to say the sides of the triangle will be in the same ratio to one another. The sides themselves might be different lengths or one triangle might be twice the size of the other, but since those two triangles are similar, the sides will be in the same ratio to each other. So, if AB is two times as long as CB, then the corresponding two sides in the other triangle will have the same relationship. In short, any two right triangles with the same angles will have sides in the same ratio, and therefore any two right triangles with sides in the same ratio will have the same angles.

So, there is a correspondence between angles in a right triangle and the ratio of sides. Since each side of the right triangle is in a ratio to one another, one side is therefore so much greater than the other and the other is so much smaller. As mentioned, the triangles have three sides-the hypotenuse and the other two named in relation to their two acute angles. In total, there are six possible ratios between the sides of a right triangle. These ratios are called the trigonometric ratios, and each of the ratios has a specific name. In relation to angle θ, the sides of the triangle can be defined as featured in Figure 3.17. The ratios are as follows:

• Sine (sin) of θ = Opposite ÷ Hypotenuse

• Cosecant (csc) of θ = Hypotenuse ÷ Opposite

• Cosine (cos) of θ = Adjacent ÷ Hypotenuse

• Secant (sec) of θ = Hypotenuse ÷ Adjacent

• Tangent (tan) of θ = Opposite ÷ Adjacent

• Cotangent (cot) of θ = Adjacent ÷ Opposite

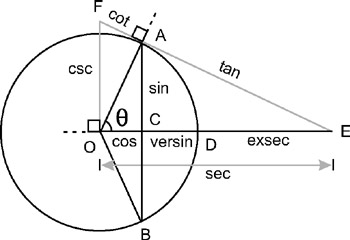
Figure 3.17

These ratios have been listed in their pairs, each of which is an inverse ratio of the other. Or, in fractional form, each is the reciprocal of the other. For example, sin and csc are opposite ratios, and so are cos and sec. The next section examines these ratios and their importance more closely.

3.9.2 Angle and Side Correspondence

From the right triangle shown here it can be seen that angle θ has an opposite side of 6 cm and an adjacent side of 8 cm. The right triangle also has a hypotenuse of 10 cm. As demonstrated in the previous section, the sine of angle θ is the ratio of the opposite side to the hypotenuse, 6 cm ÷ 10 cm. In fact, for angle θ it is possible to express all the trigonometric ratios as follows:

• Sine of θ = 6cm ÷ 10cm

• Cosecant of θ = 10cm ÷ 6cm

• Cosine of θ = 8cm ÷ 10cm

• Secant of θ = 10cm ÷ 8cm

• Tangent of θ = 6cm ÷ 8cm

• Cotangent of θ = 8cm ÷ 6cm

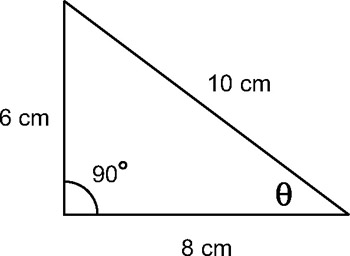
Figure 3.18

Consulting the trigonometric table in Appendix A, it can be seen that each ratio corresponds to an angle measure and, likewise, each angle corresponds to a ratio of side length. Tangent 1 is 45 degrees and cosine 60 is 0.5.

3.9.3 Side Lengths

Since angles correspond to ratios of side lengths, it is therefore possible to calculate the length of sides from certain right triangles if at least one angle and one side are known.

3.9.4 Co Functions

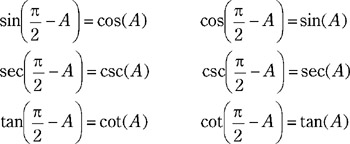
Figure 3.19

Each of the trigonometric functions-sine, secant, and tangent-has a "co" function counterpart. These are cosine, cosecant, and cotangent, hence the reason for the "co" prefix to their names. In an earlier section, the side ratios each of these functions represent was demonstrated. For example, sine represents the ratio of the opposite side to the hypotenuse. Examining these functions in more detail leads us to discover a relationship between the functions (sin, sec, and tan) and their co functions (cos, csc, and cot). In short, the function of any angle is equal to the co function of its complement angle. Remember, two angles are complements if their sum is a right angle; thus, 60 and 30 are complements in the same way 50 and 40 are complements. So, sin 60 is said to equal cos 30, and sec 40 is said to equal csc 50, and so on.