3.8 Right Triangles and the Pythagorean Theorem

3.8 Right Triangles and the Pythagorean Theorem

In order to discover the lengths of the sides of any polygon, we must measure. If we have plotted the vertices of any figure in a coordinate space, we can measure the length of the sides easily. However, in the above diagram, how can we calculate the length of the diagonal for this right triangle? Rather than simply measuring, is there a way, given the lengths of the other two sides, to obtain the length of the diagonal?

In a right triangle, the diagonal is the longest side and is called the hypotenuse. This side is always opposite the right angle. The ancient Greek mathematician Pythagoras discovered a method for calculating the length of the hypotenuse based upon the length of the other two sides. This is called the Pythagorean theorem.

The theorem is based on the idea of squares drawn onto each side of a right triangle-a square on every side, including the hypotenuse. It states that the square drawn on the hypotenuse will equal the square drawn on the other two sides. Take another look at Figure 3.16.

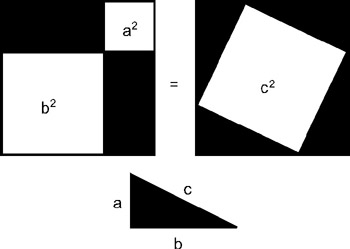
Figure 3.16

Note 

Remember, every side of a square is equal. To find the area of a square means to multiply the length of one side by itself-hence, to square a number. To find the length of one side, or rather to find the number before squaring, the square root is taken.

Therefore, the square on the hypotenuse can be calculated as follows:

• Hyp² = side1² + side2²

Notice that since we are dealing with hypotenuse squared, in order to find the length of the hypotenuse, we must take the square root.