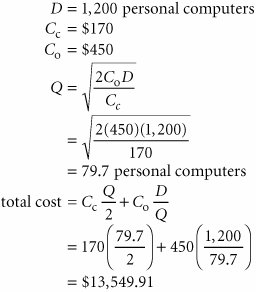Example Problem Solutions

[Page 760 ( continued )]

The following example will demonstrate EOQ analysis for the classical model and the model with shortages and back ordering.

Problem Statement

Electronic Village stocks and sells a particular brand of personal computer. It costs the store $450 each time it places an order with the manufacturer for the personal computers. The annual cost of carrying the PCs in inventory is $170. The store manager estimates the annual demand for the PCs will be 1,200 units.

1. Determine the optimal order quantity and the total minimum inventory cost.

2. Assume that shortages are allowed and that the shortage cost is $600 per unit per year. Compute the optimal order quantity and the total minimum inventory cost.

Solution

Step  1.	(part a): Determine the Optimal Order Quantity
	[Page 761]
Step  2.	(part b): Compute the EOQ with Shortages

Problem Statement

A computer products store stocks color graphics monitors, and the daily demand is normally distributed, with a mean of 1.6 monitors and a standard deviation of 0.4 monitor. The lead time to receive an order from the manufacturer is 15 days. Determine the reorder point that will achieve a 98% service level.

Solution

Step  1.	Identify Parameters = 1.6 monitors per day L = 15 days s d = 0.4 monitors per day Z = 2.05 (for a 98% service level)
Step  2.	Solve for R