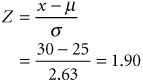Probabilistic Activity Times
| In the project network for building a house presented in the previous section, all the activity time estimates were single values. By using only a single activity time estimate, we in effect assume that activity times are known with certainty (i.e., they are deterministic). For example, in Figure 8.8, the time estimate for activity 2 (laying the foundation) is shown to be 2 months. Because only this one value is given, we must assume that the activity time does not vary (or varies very little) from 2 months. In reality, however, it is rare that activity time estimates can be made with certainty . Project activities are likely to be unique, and thus there is little historical evidence that can be used as a basis to predict actual times. However, we earlier indicated that one of the primary differences between CPM and PERT was that PERT used probabilistic activity times. It is this approach to estimating activity times for a project network that we discuss in this section. Probabilistic Time EstimatesTo demonstrate the use of probabilistic activity times, we will employ a new example. (We could use the house-building network from the previous section; however, a network that is a little larger and more complex will provide more experience with different types of projects.) The Southern Textile Company has decided to install a new computerized order processing system that will link the company with customers and suppliers online. In the past, orders for the cloth the company produces were processed manually, which contributed to delays in delivering orders and resulted in lost sales. The company wants to know how long it will take to install the new system. The network for the installation of the new order processing system is shown in Figure 8.14. We will briefly describe the activities. Figure 8.14. Network for order processing system installation(This item is displayed on page 339 in the print version)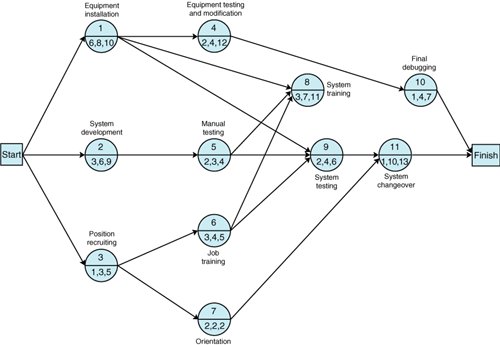 The network begins with three concurrent activities: The new computer equipment is installed (activity 1); the computerized order processing system is developed (activity 2); and people are recruited to operate the system (activity 3). Once people are hired , they are trained for the job (activity 6), and other personnel in the company, such as marketing, accounting, and production personnel, are introduced to the new system (activity 7). Once the system is developed (activity 2), it is tested manually to make sure that it is logical (activity 5). Following activity 1, the new equipment is tested , and any necessary modifications are made (activity 4), and the newly trained personnel begin training on the computerized system (activity 8). Also, node 9 begins the testing of the system on the computer to check for errors (activity 9). The final activities include a trial run and changeover to the system (activity 11) and final debugging of the computer system (activity 10). At this stage in a project network, we previously assigned a single time estimate to each network activity. In a PERT project network, however, we determine three time estimates for each activity, which will enable us to estimate the mean and variance for a beta distribution of the activity times. We assume that the activity times can be described by a beta distribution for several reasons. First, the beta distribution mean and variance can be approximated with three estimates. Second, the beta distribution is continuous, but it has no predetermined shape (such as the bell shape of the normal curve). It will take on the shape indicatedthat is, be skewedby the time estimates given. This is beneficial because typically we have no prior knowledge of the shapes of the distributions of activity times in a unique project network. Third, although other types of distributions have been shown to be no more or less accurate than the beta, it has become traditional to use the beta distribution for probabilistic network analysis. Three time estimates for each activitya most likely , an optimistic , and a pessimistic provide an estimate of the mean and variance of a beta distribution . The three time estimates for each activity are the most likely time, the optimistic time, and the pessimistic time. The most likely time is the time that would most frequently occur if the activity were repeated many times. The optimistic time is the shortest possible time within which the activity could be completed if everything went right. The pessimistic time is the longest possible time the activity would require to be completed, assuming that everything went wrong. In general, the person most familiar with an activity makes these estimates to the best of his or her knowledge and ability. In other words, the estimate is subjective. (See Chapter 11, on subjective probability.) These three time estimates can subsequently be used to estimate the mean and variance of a beta distribution. If a = optimistic time estimate m = most likely time estimate b = pessimistic time estimate the mean and variance are computed as follows : These formulas provide a reasonable estimate of the mean and variance of the beta distribution, a distribution that is continuous and can take on various shapesthat is, exhibit skewness . The three time estimates for each activity are shown in Figure 8.14 and in Table 8.3. The mean and the variance for all the activities in the network shown in Figure 8.14 are also given in Table 8.3. Table 8.3. Activity time estimates for Figure 8.14
As an example of the computation of the individual activity mean times and variances, consider activity 1. The three time estimates ( a = 6, m = 8, b = 10) are substituted in our beta distribution formulas as follows: The other values for the mean and variance in Table 8.3 are computed similarly. Once the expected activity times have been computed for each activity, we can determine the critical path the same way we did previously, except that we use the expected activity times, t . Recall that in the project network, we identified the critical path as the one containing those activities with zero slack . This requires the determination of earliest and latest event times, as shown in Figure 8.15. Figure 8.15. Earliest and latest activity times(This item is displayed on page 342 in the print version)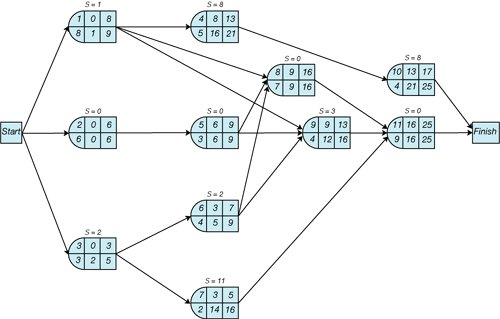 The critical path has no slack . Observing Figure 8.15, we can see that the critical path encompasses activities 2
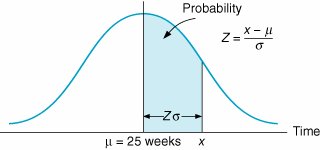
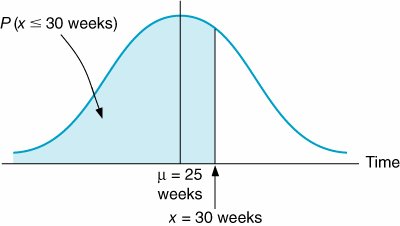
The project variance is the sum of the variance of the critical path activities . v p = 62/9 = 6.9 weeks The CPM/PERT method assumes that the activity times are statistically independent, which allows us to sum the individual expected activity times and variances to get an expected project time and variance. It is further assumed that the network mean and variance are normally distributed. This assumption is based on the central limit theorem of probability, which for CPM/PERT analysis and our purposes states that if the number of activities is large enough and the activities are statistically independent, then the sum of the means of the activities along the critical path will approach the mean of a normal distribution. For the small examples in this chapter, it is questionable whether there are sufficient activities to guarantee that the mean project completion time and variance are normally distributed. Although it has become conventional in CPM/PERT analysis to employ probability analysis by using the normal distribution, regardless of the network size , the prudent user of CPM/PERT analysis should bear this limitation in mind. The expected project time is assumed to be normally distributed based on the central limit theorem . Given these assumptions, we can interpret the expected project time ( t p ) and variance ( v p ) as the mean ( µ) and variance ( s 2 ) of a normal distribution: µ = 25 weeks s 2 = 6.9 weeks In turn , we can use these statistical parameters to make probabilistic statements about the project. Probability Analysis of the Project NetworkUsing the normal distribution, probabilities can be determined by computing the number of standard deviations ( Z ) a value is from the mean, as illustrated in Figure 8.16. Figure 8.16. Normal distribution of network duration(This item is displayed on page 343 in the print version) The Z value is computed using the following formula: This value is then used to find the corresponding probability in Table A.1 of Appendix A. For example, suppose the textile company manager told customers that the new order processing system would be completely installed in 30 weeks. What is the probability that it will, in fact, be ready by that time? This probability is illustrated as the shaded area in Figure 8.17. Figure 8.17. Probability that the network will be completed in 30 weeks or less To compute the Z value for a time of 30 weeks, we must first compute the standard deviation ( s ) from the variance ( s 2 ): Next, we substitute this value for the standard deviation, along with the value for the mean and our proposed project completion time (30 weeks), into the following formula: A Z value of 1.90 corresponds to a probability of .4713 in Table A.1 in Appendix A. This means that there is a .9713 (.5000 + .4713) probability of completing the project in 30 weeks or less. Suppose one customer, frustrated with delayed orders, has told the textile company that if the new ordering system is not working within 22 weeks, she will trade elsewhere. The probability of the project's being completed within 22 weeks is computed as follows: A Z value of 1.14 (the negative is ignored) corresponds to a probability of .3729 in Table A.1 of Appendix A. Thus, there is only a .1271 probability that the customer will be retained, as illustrated in Figure 8.18. Figure 8.18. Probability that the network will be completed in 22 weeks or less
CPM/PERT Analysis with QM for Windows and Excel QMThe capability to perform CPM/PERT network analysis is a standard feature of most management science software packages for the personal computer. To illustrate the application of QM for Windows and Excel QM we will use our example of installing an order processing system at Southern Textile Company. The QM for Windows solution output is shown in Exhibit 8.1, and the Excel QM solution is shown in Exhibit 8.2. Exhibit 8.1.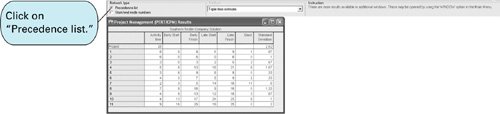 Exhibit 8.2.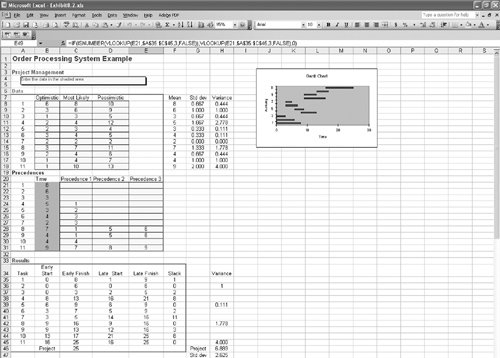 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EAN: 2147483647
Pages: 358

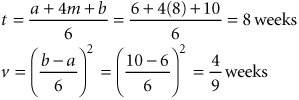
 5
5